18. Изучение сезонных колебаний.
Внутри годовые уровни многих показателей существенно зависят от сезонности (туризм, продажа сахара, сельское хозяйство, рыболовство, навигация). В таких случаях при укрупнении интервалов закономерность развития не только не проявляется, но и затушевывается. Поэтому изменение показателей в течении года анализируется при помощи индекса сезонности. В статистике существует 2 метода расчета индекса:
на основе одногодичных данных
,
где
-
значение изучаемого уровня,
на основе данных за 3 года
.
19. Понятие экономических индексов. Классификация индексов. Индивидуальные и общие индексы. Средние индексы (среднеарифметическая и гармоническая форма общих индексов).
Под индексом понимается относительная величина, количественно характеризующая динамику совокупности, состоящей из непосредственно несоединимых единиц.
Виды индексов.
Индивидуальные индексы
- рассчитываются для отдельных видов
продукции, работ и услуг. Различают
индивидуальные индексы:
качественных показателей (цена , себестоимость
,
трудоемкость
,
выработка продукции
).
Индивидуальный
индекс цены:
,
где
-
цена текущего периода,
-
цена базисного периода.
Индивидуальный
индекс себестоимости:
.
Количественных показателей (количество произведенной продукции
,
численность
)
Индивидуальный
индекс физического объема:
,
где
-
количество произведенной продукции в
текущем периоде,
-
количество произведенной продукции в
базисном периоде.
На основе
индивидуальных индексов могут быть
построены сводные индексы третьего
показателя:
-
индивидуальный индекс выручки (стоимости)
.
На основе индексов можно рассчитать абсолютное изменение показателей
Для индивидуальных
индексов цены:
физический объем
выручки:
.
Общие индексы
- агрегатные, рассчитываются, когда на
одном предприятии производится или
продается разнородная продукция. В
основе
лежат
.
.
В общих индексах качественных показателей в качестве веса – соизмерителя выступает количественный показатель ( или ) текущего периода. На основе данной формулы можно определить абсолютное изменение выручки в результате изменения цен на продукцию
.
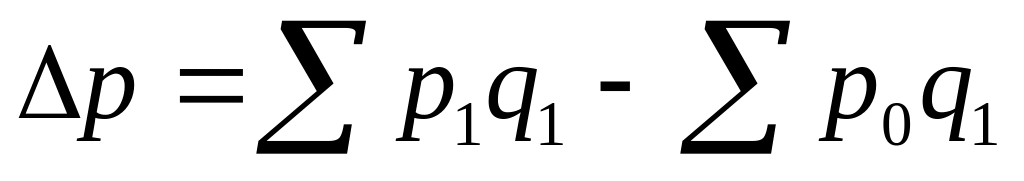Построение общего индекса для количественных показателей:
общий вид физического
объема
.
В качестве веса
соизмерителя для количественных
показателей выступает качественный
показатель на базисном уровне. На основе
данной формулы можно определить
абсолютное изменение выручки под
влиянием проданной или произведенной
продукции
.
Рассмотрим
взаимосвязь индексов качественного и
количественного показателя:
-
общий индекс выручки или стоимости или
.
На основе приведенной формулы можно
рассчитать абсолютное изменение выручки
под действием 2-х факторов: цены и
количества
.
Средние индексы – являются разновидностью общих индексов и применяются в тех случаях, когда неизвестны данные либо за базис, либо за текущий период, но известны индивидуальные индексы изучаемых величин:
Средне арифметическая
- для количественного показателя физического объема .
Под средним индексом
понимается индекс, вычисленный как
средняя величина из индивидуальных
индексов
,
в качестве
,
Средне гармоническая форма качественных показателей – индекс цены
,
,
.
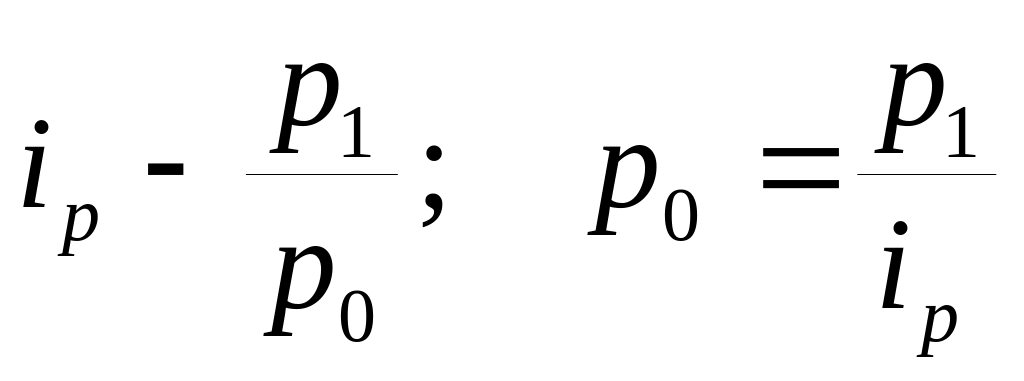