
- •Сущность статистического наблюдения.
- •2. Статистическая сводка. Группировка. Вторичная группировка.
- •3. Статистические таблицы. Графический метод представления информации.
- •Абсолютные и относительные величины: сущность, виды, порядок расчета.
- •5. Степенные средние величины.
- •6. Структурные средние величины.
- •7. Асимметрия и эксцесс.
- •8. Теоретические кривые распределения. Кривая нормального распределения и ее построение по эмпирическим данным.
- •9. Критерий согласия Пирсона «хи-квадрат». Критерии согласия Романовского, Ястремского, Колмогорова.
- •10. Понятие вариации. Абсолютные показатели вариации признака. Относительные показатели вариации признака.
- •11. Дисперсия. Свойства дисперсии. Порядок расчета. Правило сложения дисперсий. Дисперсия альтернативного признака.
- •13. Типическая и серийная выборка. Определение предельной ошибки выборки для средней и доли при повторном и бесповторном отборе.
- •14. Использование формул предельной ошибки выборки. Определение численности выборочной совокупности для собственно-случайной, механической, типической и серийной выборки.
- •15. Понятие рядов динамики их виды. Показатели рядов динамики (абсолютные и относительные). Прогнозирование и экстраполяция в рядах динамики.
- •Показатели анализа рядов динамики.
- •16. Средние показатели в рядах динамики.
- •17. Изучение основной тенденции развития (укрупнение уровней ряда, скользящая средняя, аналитическое выравнивание).
- •18. Изучение сезонных колебаний.
- •19. Понятие экономических индексов. Классификация индексов. Индивидуальные и общие индексы. Средние индексы (среднеарифметическая и гармоническая форма общих индексов).
- •20. Индексы цепные и базисные, с постоянной и переменной базой сравнения.
- •21. Индексы средних величин (индексы переменного, постоянного состава и структурных сдвигов).
- •22. Территориальные индексы.
- •23. Индексы Ласпейреса, Пааше, Лоу.
- •25. Парная регрессия для сгруппированных данных. Коэффициент эластичности.
- •26. Коэффициенты корреляции рангов Спирмена, Кэндела, Фехнера.
- •27. Методы изучения корреляционной связи качественных показателей. Расчет коэффициентов взаимной сопряженности Пирсона и Чупрова для оценки корреляционной связи качественных показателей.
- •28. Статистика населения.
- •Показатели естественного прироста
- •Показатели механического прироста (миграция):
- •29. Статистика численности и использования рабочего времени.
- •30. Статистика оплаты труда.
- •31. Статистика производительности труда.
- •Среднемесячная выработка
- •Среднемесячная выработка в расчете на одного работающего.
- •32. Социальная статистика.
- •32. Статистика основных производственных фондов.
5. Степенные средние величины.
Средняя величина – вариант x, который обладает наиболее типическими свойствами изучаемой совокупности.
Типовая формула
для расчета средней величины:![]()
![]()
если z=1, то получается ср. арифметическая
если z=0 – ср. геометрическая
если z=-1 – ср. гармоническая
если z=2 – ср. квадратическая.
Следующие виды средних величин:
Ср. арифметическая:
Простая, т.е. в совокупности все значения x (признака) встречаются по одному разу
 ,
- количество единиц в совокупности.
,
- количество единиц в совокупности.Взвешенная (средняя для сгруппированных данных), x встречается более чем один раз.
 .
.
Расчет ср. арифметической зависит от вида ряда, в интервальном необходимо найти середину интервала.
Свойства ср. арифметической:
средняя из постоянного числа равна постоянному числу.
если все частоты увеличить на одно и то же число или уменьшить, то средняя величина от этого не изменится.
если варианты x увеличить или уменьшить на постоянное число, то средняя увеличится или уменьшится на это число.
если вариант x увеличить или уменьшить в к раз, то средняя величина изменится в к раз.
Ср. гармоническая – применяется, когда неизвестна частота, а известно лишь произведение частоты на вариант (М).
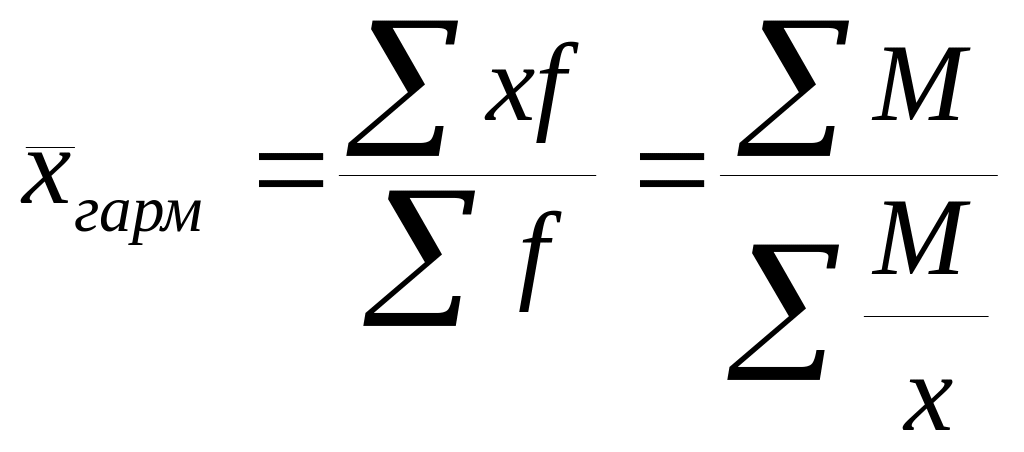 - применяется наиболее часто для расчета
средних цен.
- применяется наиболее часто для расчета
средних цен.Ср. геометрическая – рассчитывают для определения ср. темпов роста изучаемого показателя в рядах динамики.
 ,
где
,
где
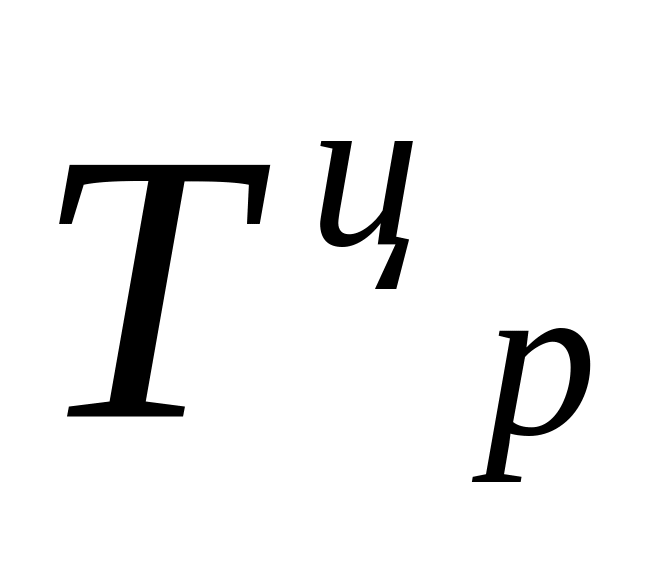 - темпы роста цепные, n
– количество уровней ряда.
- темпы роста цепные, n
– количество уровней ряда.Ср. квадратическая – используют для определения вариации ряда, под которой понимается отклонение изучаемого признака от средней величины.
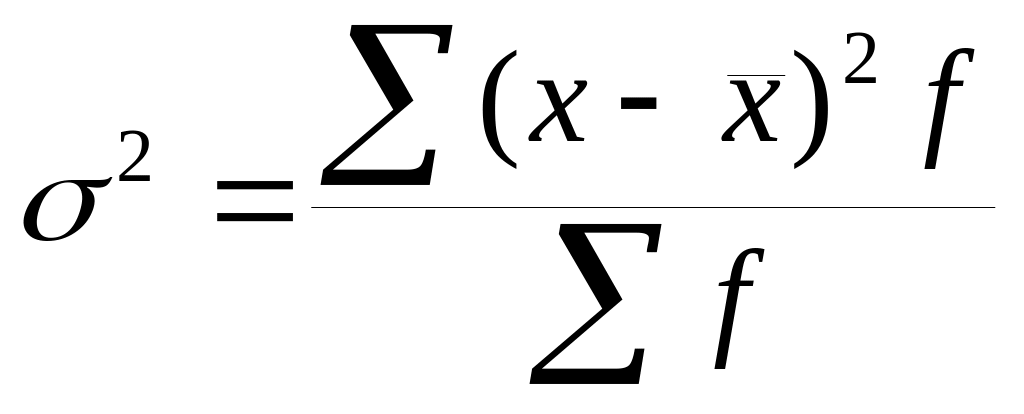 ,
где
,
где
 - ср. квадратическое (дисперсия)
- ср. квадратическое (дисперсия)
6. Структурные средние величины.
1. Мода
(![]() )
– под ней понимается наиболее часто
встречающийся вариант. Мод может быть
несколько. Расчет моды зависит от того,
в каком ряду она рассчитывается (в
дискретном или в интервалом).
)
– под ней понимается наиболее часто
встречающийся вариант. Мод может быть
несколько. Расчет моды зависит от того,
в каком ряду она рассчитывается (в
дискретном или в интервалом).
В дискретном ряду (ищем
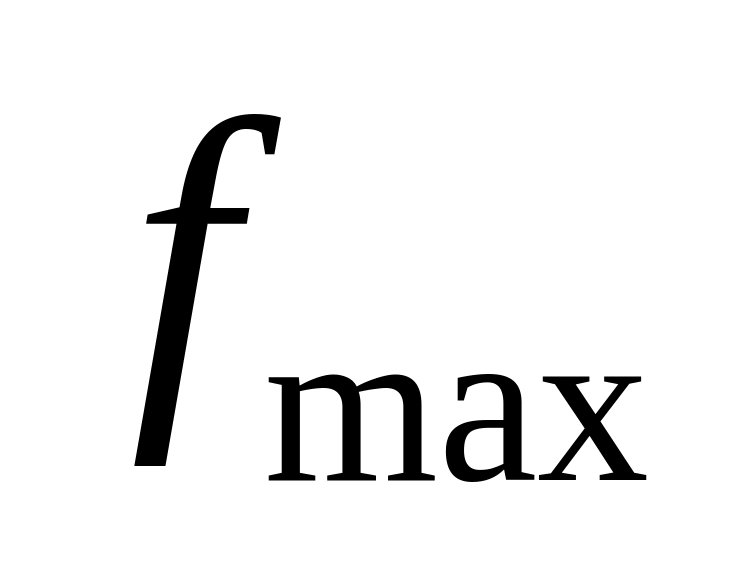 ,
находим по нему интервал и строим
полигон).
,
находим по нему интервал и строим
полигон).В интервальном ряду
Находим
Находим по модальный интервал
Находим по формуле:
 ,
где
,
где
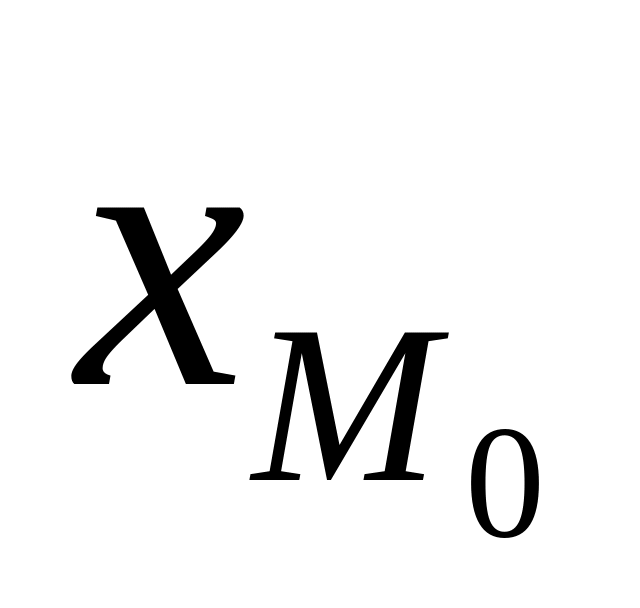 -
начало модального интервала
-
начало модального интервала
![]() -
величина модального интервала
-
величина модального интервала
![]() -
частота модального интервала
-
частота модального интервала
![]() -
частота до модального интервала
-
частота до модального интервала
![]() -
частота после модального интервала
-
частота после модального интервала
2. Медиана
(![]() )-
вариант, делящий ранжированный ряд по
полам. Для того, что бы найти медиану,
находят ее порядковый номер:
)-
вариант, делящий ранжированный ряд по
полам. Для того, что бы найти медиану,
находят ее порядковый номер:
![]() -
для четного количества.
-
для четного количества.
![]() -
для нечетного количества.
-
для нечетного количества.
Затем находят ряд накопленных частот. Расчет медианы зависит от того, в каком ряду она рассчитывается.
Для дискретного ряда: - находим
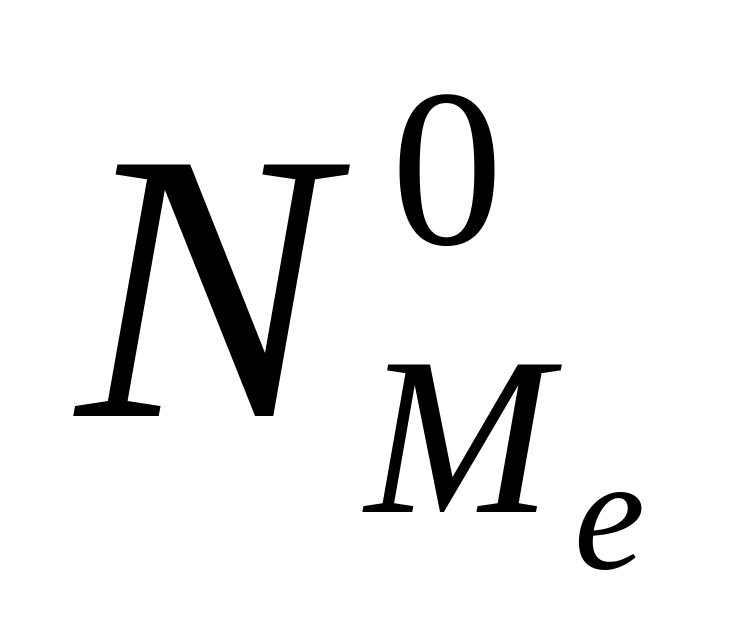
-
находим накопленную частоту
![]()
- по и находим .
Для интервального ряда. В интервальном ряду медиану рассчитывают по формуле:
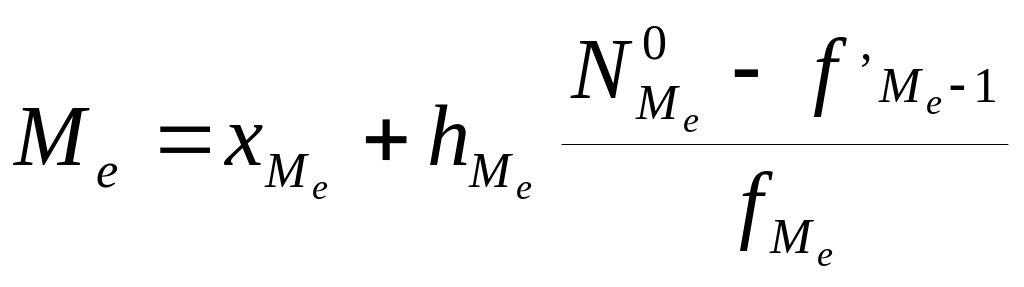 ,
где
,
где
![]() -
начало медианного интервала;
-
начало медианного интервала;
![]() -
величина медианного интервала;
-
величина медианного интервала;
![]() -
частота медианного интервала;
-
частота медианного интервала;
![]() -
частота накопленная до медианного
интервала;
-
частота накопленная до медианного
интервала;
В интервальном ряду можно рассчитывать графически, построив кумуляту по накопленной частоте.
