31. Статистика производительности труда.

Производительность труда измеряется 2-мя способами:

1. Показатель выработки – прямой показатель, представляет собой отношение выручки от продажи продукции к численности. 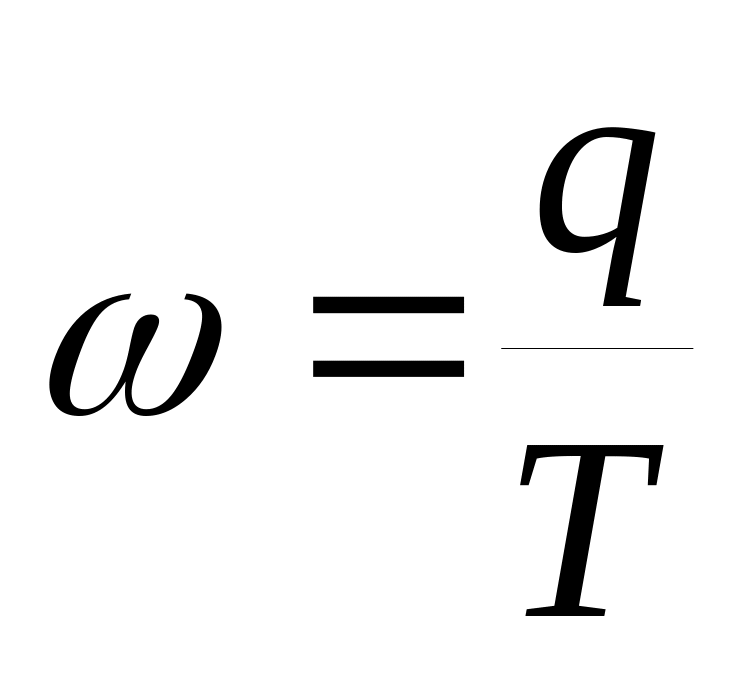, где - объем произведенной продукции, -численность.

2. Показатель трудоемкости – обратный показатель.

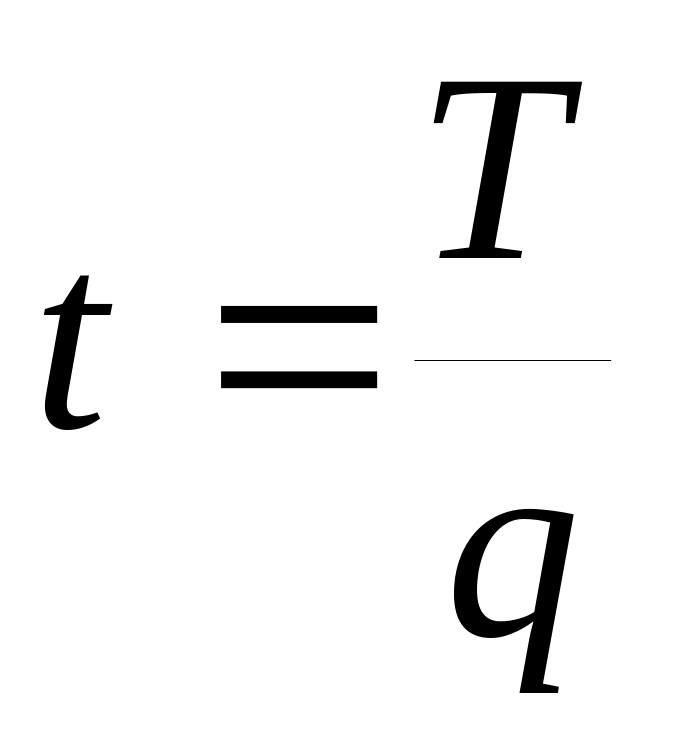
Трудоемкость может рассчитываться и в трудовых затратах, т.е. он будет показывать затраты труда на единицу произведенной продукции. Таким образом показатели производительности труда могут быть натуральными, стоимостными, трудовыми и условно- натуральными.

В зависимости от того, чем измеряются затраты труда, различают следующие уровни производительности труда:

1. среднечасовая выработка показывает среднюю выработку рабочего за 1 час фактической работы. Определяется только для рабочих.

Знаменатель не включает в себя время внутрисменных простоев и перерывов, но учитывает время сверхурочной работы;

2. средняя дневная выработка рассчитывается только для рабочих, представляет собой

3. Среднемесячная выработка

4. Среднемесячная выработка в расчете на одного работающего.

.

Для анализа производительности труда используется в основном индексный метод. Применение индексных методов:

• прямой (показатель выработки) , где - выработка в текущем периоде, 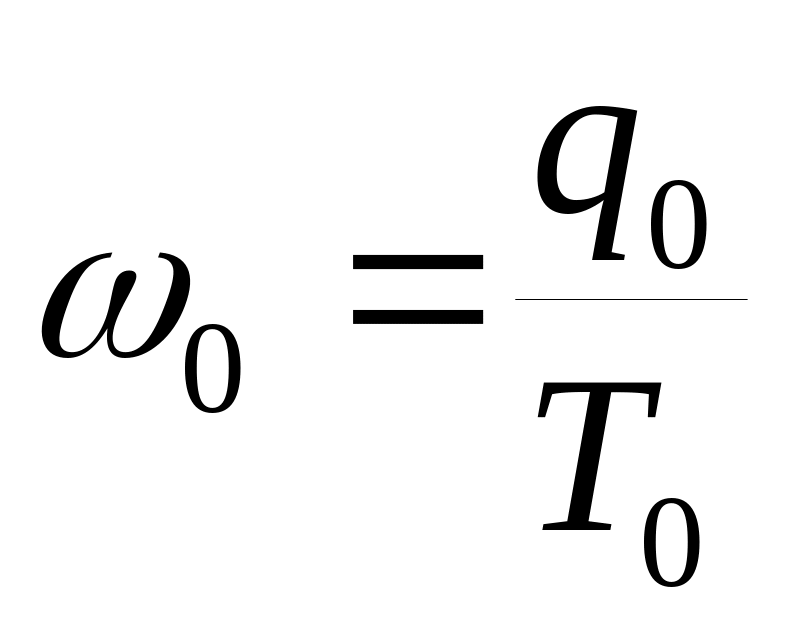- выработка в базисном;

• обратный (показатель трудоемкости) 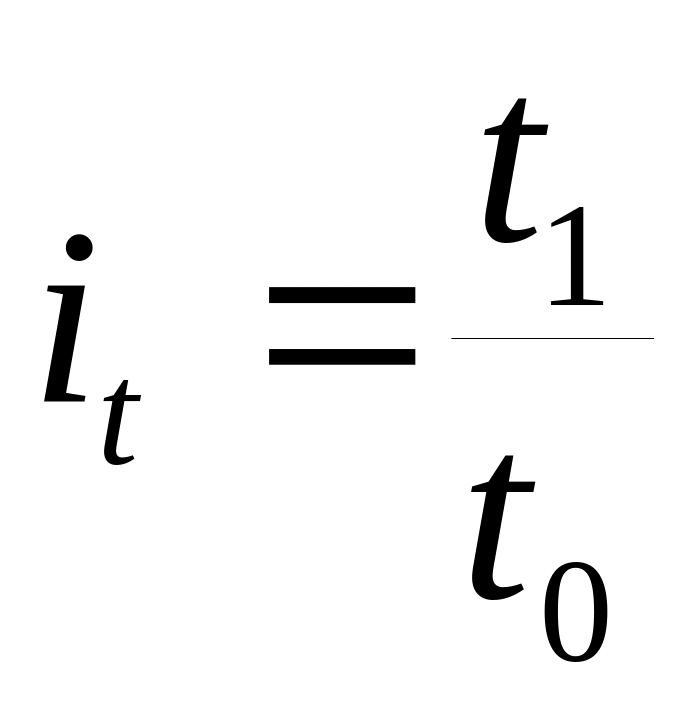, , . - затраты труда в текущем и базисном периодах.

На ряду с индивидуальными индексами используют общие индексы, по нескольким видам продукции

Применение индексов средних величин.

Они применяются в том случае, когда на разных предприятиях производится однородная продукция. В этом случае применяют индексы , и .

Для выработки	Для трудоемкости

На изменение объема производимой продукции влияют изменения производительности труда и численности работников.

- объем произведенной продукции.

Рассмотрим изменение объема производства за счет изменения производительности труда

Численности

.

В зависимости от того, в каких единицах измерения выражена продукция, а следовательно и средняя выработка, производительность труда принято называть:

1. натуральный индекс производительности труда

, - т, кг., м.

2. стоимостной индекс производительности труда

, - стоимость выпущенной продукции в руб.

3. трудовой индекс производительности труда

, - затраты времени чел/час., чел/дн..

32. Социальная статистика.

Социальная статистика изучает уровень жизни населения, денежные доходы и расходы, уровень жизни, бедности и др.

Для того, чтобы определить данные показатели, необходимо рассчитывать средние показатели по з/пл, по численности, по доходам и т.д.

Рассмотрим специфические показатели, характеризующий уровень жизни:

Коэффициент эластичности потребления в зависимости от изменения доходов

, где - начальный доход, - начальное потребление, -изменение этих показателей за некоторый период.

Данный коэффициент позволяет определить на сколько % возрастает или уменьшается потребление товаров или услуг при росте дохода на 1 %.

Если , то качество товара принято считать низким.

Если , то потребление растет быстрее доходов.

Если , то между доходами и потреблением пропорциональная зависимость.

Если , то потребление увеличивается меньше чем доход.

К основным характеристикам дифференциации доходов населения относится:

1. – модальный

- медиальный

- средний уровень доходов;

2. коэффициент концентрации доходов (Джини);

3. коэффициент дифференциации доходов.

Коэффициент Джини - показывает распределение всей совокупности (сумы) доходов между отдельными группами.

- доля населения принадлежащая к i социальной группе

- доля доходов в i социальной группе

- кумулятивная доля доходов.

При равномерном распределении доходов стремится к 0. Чем больше различия доходов, тем ближе к 1.

Для графического изображения неравномерности доходов строят кривую Лоренца. Для того, чтобы построить данную кривую, население делится на 20 % группы.