25. Парная регрессия для сгруппированных данных. Коэффициент эластичности.

При множественной регрессии на результативный признак влияет несколько факторов. Построение уравнения регрессии состоит из нескольких этапов:

выбор формы связи (которое описывается уравнением регрессии). Наиболее приемлемый способ выбора связи, заключается в переборе различных уравнений. Сущность этого метода заключается в том, что при помощи средств вычислительной техники, с помощью специальных программ рассчитывается уравнение регрессии с последующей статистической проверкой на соответствие критерия Стьюдента и Фишера, которые являются табличными. Этот метод очень трудоемкий и в основе все модели стараются свести к линейным.
отбор факторных признаков. Сложность их отбора заключается в том, что практически все они связанны между собой. На данном этапе возникает проблема оптимального выбора факторных признаков.

Для выбора факторных признаков используют следующие методы:

- метод экспортных оценок – основан на ранговой зависимости;

- шаговая регрессия – сущность в том, что последовательно в уравнении регрессии включается по одному факторному признаку и рассчитываются критерии, определяющие их значимость.

Коэффициент эластичности.

Для расчета влияния факторного признака на результативный применяется коэффициент эластичности. Он рассчитывается как для каждой точки совокупности, так и для всей совокупности в целом. Коэффициент эластичности показывает, насколько процентов изменится результативный признак при изменении факторного признака на 1 %.

26. Коэффициенты корреляции рангов Спирмена, Кэндела, Фехнера.

Существует несколько метод определения тесноты корреляционных связей как для количественных, так и для качественных показателей.

При помощи коэффициента корреляции, основанный на ранжировании:

Коэффициент Кэндела – в основе лежит оценка меры соответствующей последовательности ранга. При этом для каждом ранга определяется число следующих за ним значений ранга, превышающих его величину. Сумму чисел таких превышений обозначают за Р и учитывают со знаком «+». Аналогично рассчитывают для каждого ранга число следующих за ним значений меньше его величины, такую сумму обозначают за Q и учитывают с «-». 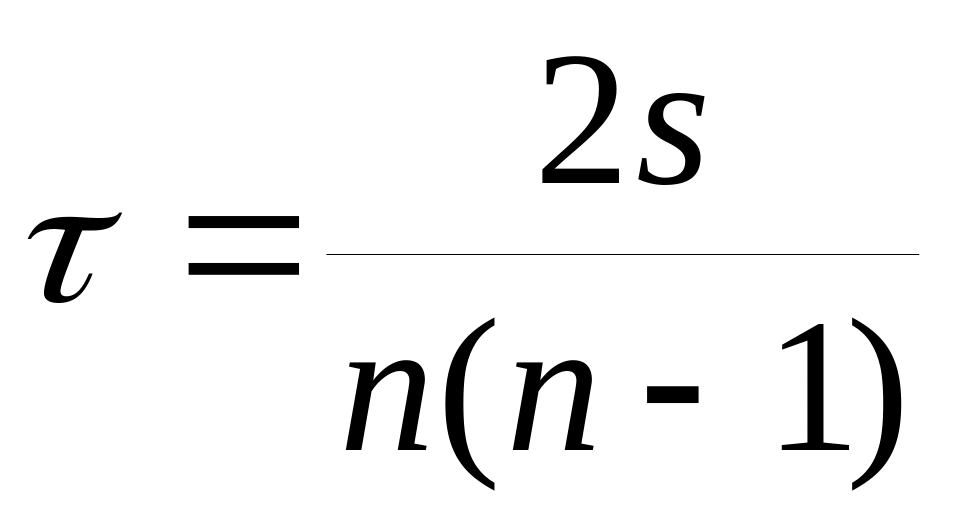, где , - количество рассматриваемых групп.
Коэффициент Спирмена используют для рядов, имеющих повторные значения. Для расчета ранжируем x и y. Если встречаются одинаковые значения, то каждому значению присваивается ранг, который равен частному отделению суммы рангов, приходящихся на эти значения, не число этих равных значений. Затем полученные ранги по x и y сравниваются между собой. , .
Коэффициент Фехнера – строится на сравнении поведения отдельных вариантов от их средней величины (по x и y). При этом во внимание принимается не величина отклонений, а их значения. ;

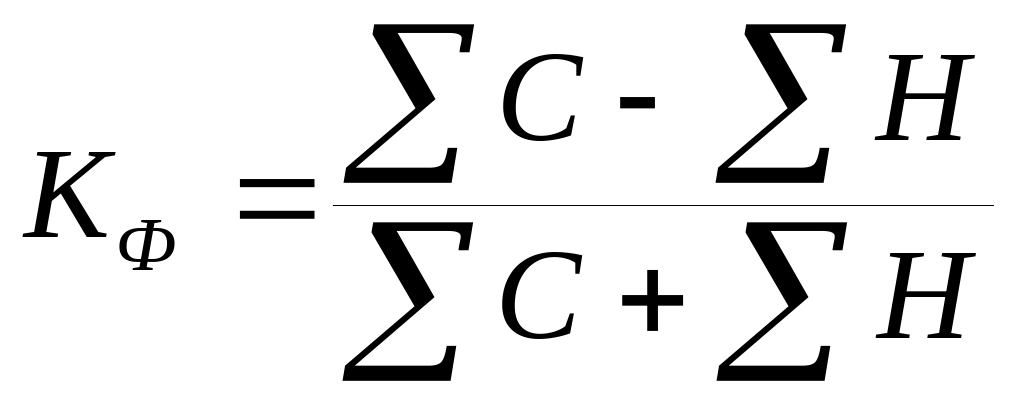- количество совпавших значений

- количество несовпавших значений.

27. Методы изучения корреляционной связи качественных показателей. Расчет коэффициентов взаимной сопряженности Пирсона и Чупрова для оценки корреляционной связи качественных показателей.

При исследовании степени тесноты связи между качественными признаками, каждый из которых представлен в виде альтернативных признаков используется следующая расчетная таблица:

a	b	a+b
c	d	c+d
a+c	b+d	a+c+b+d

Данная таблица используется, если рассматриваются 2 фактора.

Для того чтобы охарактеризовать тесноту связи, рассчитывают два коэффициента:

коэффициент ассоциации: , если связь существует, то данный коэффициент .
коэффициент контингенции: .

Если рассматриваются больше чем 2 взаимосвязанных фактора, то в этом случае рассматриваются коэффициенты взаимной сопряженности Пирсона и Чупрова.

- это показатель взаимной сопряженности, его рассчитывают как сумму соотношений квадрата частот каждой клетки расчетной таблицы к произведению итоговых частот столбца и строки -1.