23. Индексы Ласпейреса, Пааше, Лоу.

Индекс цен Ласпейреса – в качестве веса соизмерителя используется физические объемы в базисном периоде. Индекс Ласпейреса показывает, во сколько раз товары базисного периода подорожали за счет изменения цен в текущем периоде, при изменения объема потребительской корзины в текущем периоде. Индекс Ласпейреса и Пааше используются для определения темпов инфляции. На Западе и на Американском континенте для определения индекса инфляции используют индекс Ласпейреса. У нас с началом 90-х годов используют индекс Ласпейреса вместо Пааше..

- Ласпейреса

-Пааше.

Индекс Лоу учитывает изменение в ассортиментной политике.

, где .

Идеальный индекс Фишера – экономическое содержание данный индекс не имеет, чаще всего он используется для исчисления индексов цен за длительный промежуток времени, так как за это время сглаживается тенденция в составе и структуре цены.

.

24. Понятие корреляции и регрессии. Основные задачи применения корреляционно-регрессионного анализа. Корреляционная таблица. Парная регрессия. Измерение тесноты связи при помощи линейного коэффициента корреляции.

Данный анализ используется для изучения взаимосвязи между результативным и факторным признаком.

Корреляция – определяет количественную зависимость между факторным и результативным признаком.

Регрессия – определение функциональной зависимости между результативным и факторным признаком (определят уравнение регрессии характеризующий вид связи).

Рассчитывается коэффициент корреляции: по шкале Чеддока определяется теснота связей между факторным и результативным признаком.

• если коэффициент корреляции 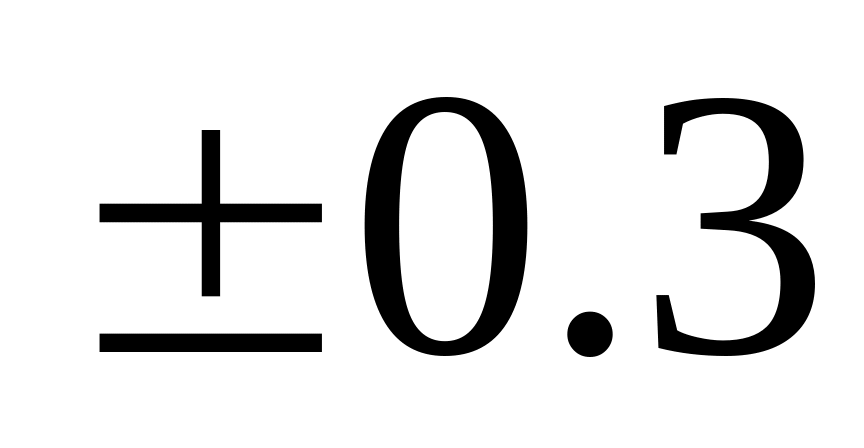- связь слабая;

• если от до - средняя;

• если от до 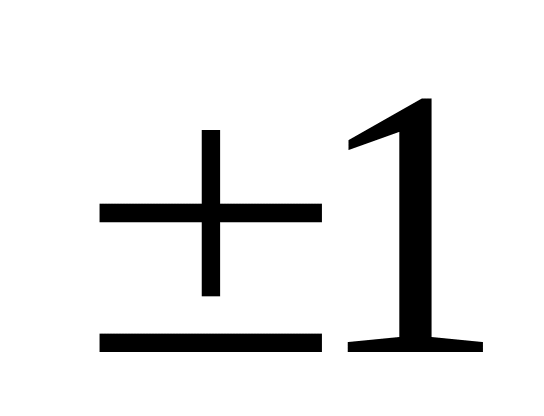- высокая, тесная.

Парная регрессия.

При парной регрессии изучается связь между результативным и одним факторным признаком. Связь между этим может быть:

- линейная

- гиперболическая

- параболическая.

Определить тип уравнения можно исследуя зависимость графически. Однако существует более общие принципы:

1. если результативный и факторный признак возрос одинаково, примерно в арифметической прогрессии, то связь между ними линейная, при обратной связи, связь гиперболическая;

2. если факторный признак увеличился в арифметической прогрессии, а результативный увеличился значительно быстрее, то используется параболическая или степенная регрессия.

Рассмотрим линейную регрессию.

- параметры данного уравнения находятся по методу наименьших квадратов ,

- представляет собой усредненное влияние на результативный признак неучтенных факторов;

- коэффициент регрессии, который показывает, насколько изменится в среднем результативный признак при увеличении факторного на единицу собственного измерения.

Корреляционная таблица.

Н а практике часто исследуются совокупности, в которых и x и y представлены в виде интервальных рядов. В этом случае в отличии от предыдущего вида значений.

y x	0-2	2-4	4-6	Итого по y
10-12	1
12-14	8	10
14-16			12
Итого по x

Если в корреляционной таблице частоты которые расположены по диагонали, тол связь между x и y будет прямая , если - связь обратная. Если частоты расположены вокруг диагонали, то это говорит о наличии связи. Если клетки таблицы заполнены большими числами то связь слабая. Если между значениями в таблице большие промежутки, значения разбросаны хаотично, то связь отсутствует.

Линейный коэффициент корреляции.

Данный коэффициент - позволяет определить количественную связь между результативным и факторным признаком.

1. , , .

2. .

3. .