Расчет заклепочных соединений по допускаемым напряжениям

Cводится к тому, чтобы соблюдалось два условия прочности:

1) на срез: τ ≤ [τ], [τ] ≈ 140 МПа.

2) на смятие σ_см ≤ [σ_см], [σ_см] ≈ 320 МПа.

Пример 1. Стержень фермы, растянутый силой Р=210 кн, со­ставлен из двух полос сечением 120x8 мм и прикреплен к фасонному листу (толщина δ = 12 мм) тремя заклепками диаметром d=20 мм (рис. 11). Найти наибольшее нормальное напряжение, возникающее в по­перечном сечении стержня (без учета концентрации напряжений) и проверить прочность заклепочного соединения на срез и смятие. Материал полос и фасонного листа Ст. 3, материал заклепок Ст. 2 закл.

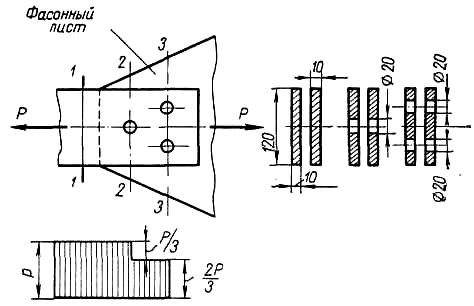
Рис. 11.

Решение. Сечение 1–1 не ослаблено заклепочными отвер­стиями. Площадь этого сечения

F_6p = 2·12·0,8·19,2 см².

Сечение 2–2 ослаблено одним отверстием. Часть площади, приходящаяся на ослабление,

F₀ = 2·2·0,8 = 3,2 см².

Площадь сечения 2–2 равна:

F_нт = F_6p – F₀ = 19,2 – 3,2 = 16 см².

Сечение 3–3 ослаблено двумя отверстиями, а площадь

F_нт = F_6p – 2F₀ = 19,2 – 2·3,2= 12,8 см².

Сила Р передается от полосы фасонному листу через три за­клепки, каждая из которых воспринимает 1/3 Р. В сечении 2–2 заклепка снимает с полосы и передает листу 1/3 Р, следовательно, между сечениями 2–2 и 3–3 полоса растянута силой, равной 2/3 Р. В сечении 3–3 две заклепки передают эту силу листу и потому правее сечения 3–3 полоса свободна от нагрузки. Усилия в полосе представлены на эпюре.

Напряжение в сечении 1–1

напряжение в сечении 2–2

напряжение в сечении 3–3

Значит, наибольшее напряжение возникнет в сечении 2–2, несмотря на то, что это сечение ослаблено одним отверстием, а сечение 3–3 двумя.

Сила, приходящаяся на одну заклепку,

Все заклепки двухсрезные. Площадь среза каждой заклепки

Напряжение среза

Условие прочности на срез соблюдается, но с излишним запа­сом, однако принять ближайший меньший диаметр заклепки (d = 17 мм) нельзя, так как тогда напряжение значительно пре­высит допускаемое.

В рассматриваемом соединении толщина фасонного листа меньше суммарной толщины двух полос, поэтому напряжение смятия будет большим в средней по высоте части заклепки. Услов­ная площадь смятия

F_см = δ·d = 1,2·2 = 2,4 см²

Напряжение смятия

Условие прочности на смятие также удовлетворяется:

σ_см = 292 МПа < [σ_см] = 320 МПа.

Следовательно, выбор диаметра заклепок сделан правильно.

Наибольшее растягивающее напряжение, возникающее в опас­ном сечении склепываемых полос, найдено в указанном примере и удовлетворяет условию прочности на растяжение с большим запасом:

σ = 131 МПа < [σ] = 160 МПа.

Пример 2. Стержень мостовой фермы, состоящий из двух швеллеров № 16, соединен с фасонным листом (косынкой) узла фермы заклепками диаметром d = 20 мм (рис. 12, а). Определить требуемое число заклепок, если действующая в стержне фермы сила P = 350 кН, толщина стенки швеллера δ = 5 мм, толщина листа косынки δ_к = 8 мм. Допускаемые напря­жения [σ_р] = 160 МПа, [σ_см] = 280 МПа, [τ_ср] = 120 МПа.

Проверить прочность стержня по ослабленному сечению.

Решение. Определим допускаемую силу на одну заклепку из условия ее прочности на срез (при этом учитываем, что в данном случае заклепки работают на срез в двух поперечных сечениях):

[Q_cр] = [τ_ср]·2πd²/4= 120·2·3,14·20²/4 = 75,36·10³ Н.

Рис. 12.

Допускаемую сила на одну заклепку из условия прочности на смятие будем определять для косынки, так как ее толщина меньше суммарной толщины двух стенок швеллеров:

[Q_см] = [σ_см]·dσ_к = 280·20·8 = 44,8·10³ Н.

Так как [Q_см] < [Q_cp], то требуемое число n заклепок определяем из усло­вия прочности на смятие:

n = P/[ Q_см] = (350·10³)/(44,8·10³) = 7,81.

Принимаем число заклепок n = 8.

Проверяем напряжение в ослабленном сечении 1–1 швеллера (рис. 12, б); по ГОСТ 8240–89 площадь сечения одного швеллера № 16 F = 18,1 см²:

Таким образом, условие прочности выполнено.