Лекция № 7

Тема 4. Сдвиг

4.1. Чистый сдвиг как частный случай плоского напряженного состояния. Закон Гука при сдвиге. Модуль сдвига

Полная деформация любого тела складывается из линейной ε и угловой деформации γ. Линейная деформация ε вызывается нормальными напряжениями σ. Угловая деформация γ вызывается касательными напряжениями τ. Связь между σ и ε изучалась ранее (растяжение-сжатие). Здесь изучается связь между τ и γ.

Сначала всегда происходит упругая де­формация сдвига и только потом разрушение тела в виде пластической деформации среза.

Чистым называется сдвиг, при котором есть сечения, где отсутствуют нормальные напряжения. При сдвиге, вызванном двумя силами, направленными навстречу друг другу, материал в промежутке между силами, кроме сдвига, еще испытывает изгиб, вызывающий появление нормальных напряжений. Примером чистого сдвига является кручение.

В сплошном материале деформацию сдвига можно осуществить, например, если подвергнуть кручению тонкостенную трубу (рис. 1, а). Прямоуголь­ные до деформации элементы материала стенок трубы превращаются в параллелограммы за счет изменения первоначально прямого угла на малый угол у, называ­емый углом сдвига.

На рис. 1, б показан элемент, выделенный из стенки трубы.

Рис. 1. Стенки трубы при закручивании испытывают деформацию сдвига

Как пример сдвига можно рассмотреть напряжения по косым площадкам в растянутом стержне (см. лекцию 2). При этом было установлено, что по любой наклонной площадке II–II, кроме касательных напряжения τ, в плоскости этой площадки возникают и нормальные напряжения σ.

И все другие примеры, приведенные на протяжении курса, показывают, что сдвиг не возникает как самостоятельное явление: обычно он сопровождает какую-либо другую основную деформацию.

Возьмем брус, заделанный одним концом и нагружен­ный на другом силой Q (рис. 2, а). Такой брус испыты­вает два вида воздействий: изгиб и сдвиг. Для умень­шения влияния изгиба брус должен быть очень коротким и толстым. При таком усло­вии изгибом можно пренеб­речь.

Под действием силы Q брус деформируется. Каждый тонкий слой, выделенный двумя смежными поперечными сечениями, сдвинется вниз и тем больше, чем дальше сечение находится от заделки. Прямоуголь­ная форма бруса abсd после деформации примет форму параллело­грамма ab'c'd.

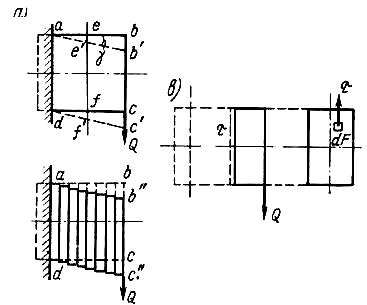
Рис. 2. Деформация бруса.

Наиболее наглядно эту деформацию можно представить, если предположить, что брус составлен из отдельных вертикаль­ных пластинок одинаковой толщины, склеенных между собой упругим клеем (рис. 2, б). Сила Q передается справа налево от места ее приложения до заделки, переходя последовательно с од­ной воображаемой пластинки на другую. При этом каждая пла­стинка сдвигается на некоторую одну и ту же величину относи­тельно лежащей слева соседней с нею пластинки. Получается ступенчатая форма сдвига. Если вообразить, что пластинки бе­рутся все тоньше и тоньше, а число их соответственно увеличи­вается, то в пределе ступенчатая линия ab" превратится в наклон­ную прямую ab' (рис. 2, а).

Так как в рассматриваемом брусе в действительности не про­исходит расслоения, то в каждом поперечном сечении возникают внутренние силы, лежащие в плоскости сечения и уравновеши­вающие внешнюю силу Q. Равнодействующая их по условию равновесия равна силе Q и противоположна ей по направлению, а интенсивность их в каждой точке сечения является касательным напряжением τ.

Деформацию сдвига можно наблюдать при работе ножниц. Эта деформация вызывается двумя равными и противоположно направленными силами, перпендикулярными к оси бруса, лежащими близко друг к другу. В очень узкой области между ножами создается область сдвига. Вырежем в этой области элемент тела и рассмотрим его деформацию (рис. 3). Грани элемента смещаются друг относительно друга под действием поперечной силы Q.

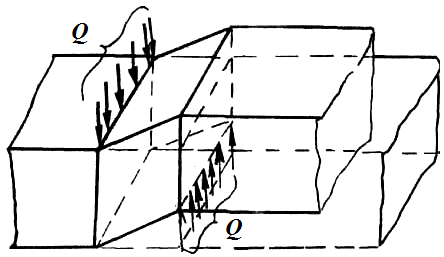
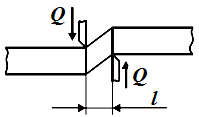
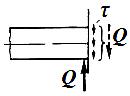
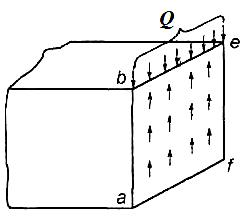
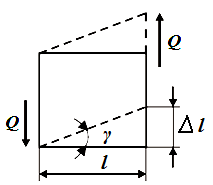
Рис. 3.

На рис. 3 показано, как действуют внешние нагрузки на элемент при деформации сдвига. Под действием силы Q элемент пре­терпевает абсолютный сдвиг ∆l.

Отношение абсолютного сдвига к расстоянию между линиями действия сил l принято называть относительным сдвигом.

Относительный сдвиг представляет собой

tg γ = ∆l/l

Учитывая, что нами рассматривается упру­гая деформация сдвига, при которой величина уг­ла γ незначительна (tg γ ≈ γ), то

γ = ∆l/l

Таким образом, сдвиг определяется угловым перемещением.

Из рис. 3 видно, что внешняя нагрузка приложена по прямой. Внут­ренние упругие силы будут уравновешивать внешнюю нагрузку. Применяя ме­тод сечений и предполагая, что внутренние упругие силы равномерно распре­делены по сечению, можно найти величину касательного напряжения, дейст­вующего по этому сечению. Для этого спроектируем все силы на вертикаль (рис. 8.1.3), что даст уравнение проекций на ось у:

∑у = 0; ­– Q + ∫τdF = 0.

F

Так как это уравнение можно представить в виде Q = ∫τdF , то если предположить, что внутренние силы располагаются равномерно по площади сечения, тогда Q = τF, откуда величина касательных напряжений при сдвиге определится по формуле

τ = Q/F

где F – площадь сечения, испытывающего деформацию сдвига.

При упругих деформациях эксперимен­тально установлена и теоретически обоснована прямая пропорциональная зависимость между ве­личиной касательного напряжения τ и величиной соответствующего ему относительного сдвига γ:

τ = Gγ,

которую принято считать законом Гука при сдвиге.

Характерно, что для многих материалов предел текучести при сдвиге τ_т связан с преде­лом текучести при растяжении следующим соотноше­нием: τ_т ≈ σ_т/√3.

Касательное напряжение на гранях элемента изменяется по довольно сложному закону, а на практике принимается постоянным. Хотя это и не верно, но допустимо. В практических расчетах ошибка компенсируется поправочными коэффициентами.

Величина G носит название модуля сдвига. Ввиду того, что относительный сдвиг – величина безразмерная, модуль сдвига имеет размерность напряжения, т. е. измеряется в Мпа.

Модуль сдвига – константа материала, которая определяется опытным путем и приводится в справочниках.

Мы рассмотрели три упругие постоянные материала: модуль Юнга E, модуль сдвига G, коэффициент Пуассона μ. Между ними существует теоретическая связь

Зависимость подтвер­ждается экспериментально. Например, для большинства сталей справочные значения E = 2·10⁵ Мпа, μ = 0.3, G = 8·10⁴ Мпа. Формула дает значение G = 7,7·10⁴ Мпа.

Из закона Гука при сдвиге, подставив в него выражения для τ и γ

τ = Gγ, Q/F = G(∆l/l)

можно получить выражение для абсолютного сдвига

∆l = Ql/GF

т. е. абсолютный сдвиг прямо пропорционален действующему усилию Q и рас­стоянию между линиями действия сил l и обратно пропорционален жесткости при сдвиге GF.

Итак, приведены формулы для определения отно­сительного сдвига, напряжения и абсолютного сдвига:

γ = ∆l/l; τ = Gγ; τ = Q/F и ∆l = Ql/GF

Если сравнить полученные формулы с выражениями для деформации рас­тяжения или сжатия, то обнаружится много общего, так как относительное удли­нение, напряжение и абсолютное удлинение определяются из зависимостей:

ε = ∆l/l; σ = Eε; σ = P/F и ∆l = Pl/EF.

Внимательное сопоставление этих формул позволит облегчить их запо­минание.