2.3 Вычисление базисного условия. Рассчитываем Wбаз по формуле:

W_баз= (14)

где 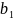- значение базисной стороны β_2-3=2470,48м, а значение рассчитывается по формуле:

= ∙ (15)

=2470,483∙0,909403587=2246,666м

Рассчитываем W_баз=

Допустимое значение W_баз рассчитывается по формуле:

W_баз^доп = ±2,5∙ m_β∙ (16)

Вычисляем W_баз^доп = 2,5∙2,6∙ = ±10,14’’

W_баз< W_баз^доп

Все вычисления сводятся в Таблицу 8.

3. Окончательное уравнивание.

Основной задачей окончательного уравнивания является получение вероятнейших значений координат пунктов сети.

Составляем ведомость уравнивания (Таблица 9). В 3 графу таблицы записываем значения углов, взятые из Таблицы 6, в графу 4 – поправки, взятые также из Таблицы 6, но таким образом, чтобы избавиться от десятых долей секунд в измеренных углах.

Например для угла 2, значение которого 52°42'52,2'', поправка будет равна -1,2’’; для угла 3, значение которого 98°56'14,3'', поправка равна -1,3’’; для угла 1, значение которого 28°20'57,1'', поправка равна -1,1’’.

Чтобы рассчитать первичные поправки i₂ в графе 5, необходимо рассчитать вторичные поправки за условие горизонта. Для этого составляем Таблицу 10. В Таблицу 10 заносим значения углов 3, 6, 9, 12, 15, 18, взятые из Таблицы 6, а значения поправок i₁ берем из Таблицы 9. Для нахождения вторичных поправок за условие горизонта складываем значения измеренных углов, затем складываем значения исправленных углов и находим невязку, чтобы окончательно распределить вторичные поправки.

Вернемся к Таблице 9. В каждый связующий угол А_kи В_k в каждом треугольнике вводим поправку с обратным знаком равную половине поправки за условие горизонта в центральный угол, принадлежащий главному треугольнику, но так чтобы сумма двух поправок связующих углов была равна центральной поправке. Эти значения записываем в графу 5. Вторичные поправки вычисляются по первично-исправленным связующим углам. Для этого рассчитываем Таблицу 11. Отдельно записываем и рассчитываем Sin и ctg углов группы А_k и В_k, при этом значения Sin округляем до 6 знаков после запятой, а значения ctg – до тысячных долей.

Находим преобразованный свободный член по формуле:

W_n’ = (17)

где - произведение синусов группы А_k

– произведение синусов группы В_k

W_n’ = = 54,9’’

Находим значение ∑ g А_k²+g В_k²=37,06925999

Рассчитываем допустимое значение свободного члена по формуле:

W_n’^доп = ±2,5∙ m_β∙ (18)

W_n’^доп = ±2,5∙ 2,6∙6,088453004=39,57’’

В нашем случае W’_n> W_n’^доп, тогда рассчитаем W_n’^доп для триангуляции I класса (m_β=5’’) и для триангуляции II класса (m_β=10’’) и сравним с полученным W’_n.

W_n^доп=±76,106’’ – для I класса

W_n^доп=±152,211’’ – для II класса

Для нахождения значения вторичных поправок необходимо рассчитать карелату по формуле:

k= (19)

k= = 1,4809’’

Рассчитываем вторичные поправки по формуле:

А_k = - В_k = k∙ (g А_k+g В_k) (20)

В связующие угла группы А_k вводят поправку из Таблицы 11 с тем же знаком, а в углы группы В_k – ту же поправку, но с противоположным знаком. В центральные углы поправки не вводятся.

Затем рассчитываем по уравненным углам окончательное значении стороны, используя теорему синусов. Контролем служит вычисление исходной стороны, которое не должно отличаться от заданного значения более чем на 5 м.

Окончательное значение координат пунктов теодолитного хода рассчитываем в Таблице 12.

Вывод.

Вывод о том к какому классу относятся сети триангуляции можно сделать по значениям длин сторон, значению средней квадратической ошибки измеренного угла, предельной допустимой невязки в треугольнике, а также по значению относительной ошибки исходной (базисной) стороны. В нашем случае сети триангуляции 2 класса.