
- •Лекция №1 Глава1. Датчики температуры
- •1.1 Температура как физическая величина
- •Опорные точки шкалы мптш
- •1.2. Понятие о теплообмене
- •1.4.Динамические характеристики датчиков температуры
- •1.7. Измерительные цепи терморезисторов
- •1.8. Термоэлектрический метод
- •Измерительные цепи термопар
- •2.3. Капиллярный метод
- •2.4. Вискозиметры с падающим телом
- •2.5. Ротационный метод
1.4.Динамические характеристики датчиков температуры
В общем случае термодинамическое состояние тела описывают уравнением теплопроводности
![]() , где
, где
а = λ /(сγ) – коэффициент температуропроводности;
c[BT · c/(кг · к)] – удельная теплоемкость;
λ – теплопроводность;
γ – плотность.
Из решения этого уравнения находят распределение температуры по всему объему тела. Для датчиков сложной формы, выполненных из материалов с разными теплофизическими свойствами, нахождение распределения температуры является сложной математической задачей. Обычно датчики температуры имеют небольшие размеры, а интенсивность теплообмена со средой невелика. В этом случае температуру во всех точках датчика можно считать постоянной. Кроме того, будем считать, что теплофизические свойства датчиков (теплоемкость, коэффициент теплоотдачи) не зависит от температуры. Наконец. Примем, что теплоотдача пропорциональна разности температур (Тп-Тср), что справедливо для теплопроводности, вынужденной и естественной конвекции при малых разностях температур.
При таких допущениях динамические характеристики датчика можно получить из анализа уравнения его теплового баланса. Согласно этому уравнению вся теплота, поступающая к датчику массой m или теряемая им в единицу времени вследствие теплообмена, идет на изменение его теплосодержания, т.е. запасенного количества тепла QП=СПТП.
Здесь СП=сm- теплоемкость преобразователя, а ТП – его абсолютная температура.
Изменения теплосодержания в единицу времени определяется тепловыми потоками за счет теплопроводности, конвекции и излучения
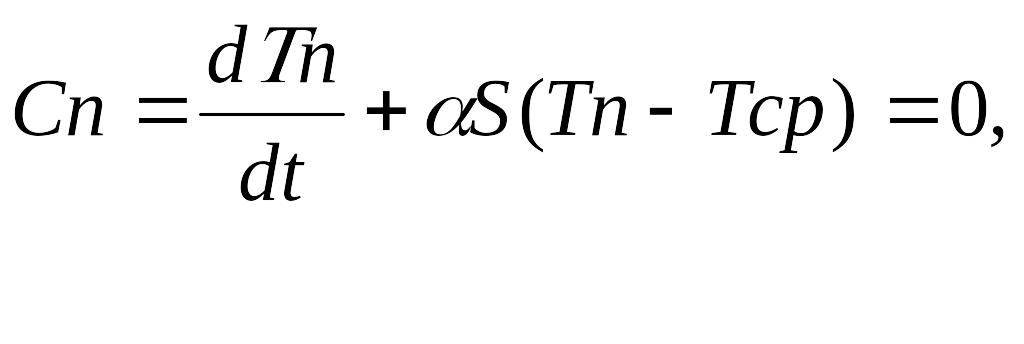 или
или
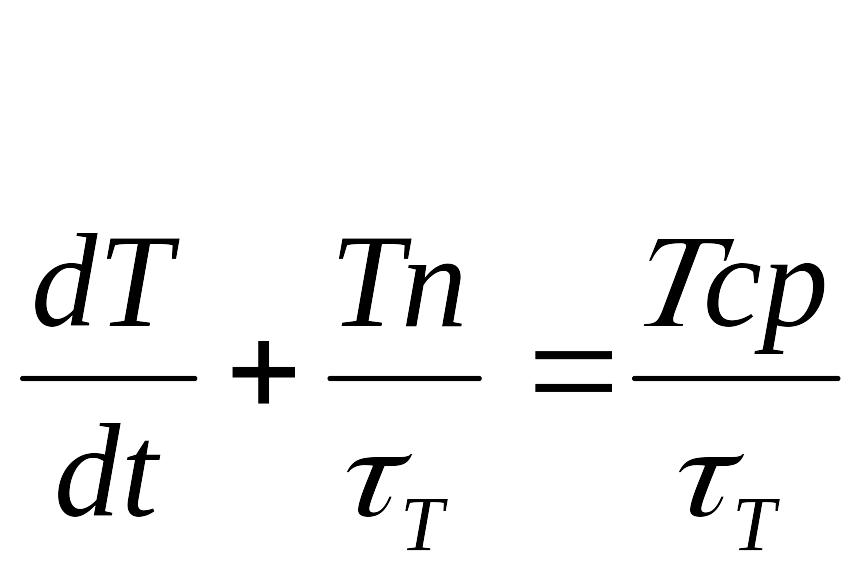 , (Δ) где
, (Δ) где
τт = Rт· Сп – тепловая постоянная времени называется показателем или постоянной термической инерции (тепловое сопротивление RT = 1/(LS) учитывает суммарный вклад в перенос тепла теплопроводности, конвекции и излучения).
Получено дифференциальное уравнение аналогично уравнению электрических цепей первого порядка. Поэтому рассматриваемую тепловую цепь можно моделировать RC- цепью, включенной последовательно с источником ЭДС E(t). Ее поведение описывается дифференциальным уравнением
![]()
Следовательно, можно считать, что переход от тепловой цепи к электрической осуществляется заменами:
TП ИС RT R CП С
Темп Тепл. Теплоемкость
преобразователь сопротивление преобразователя
Рассмотрим переходную характеристику датчика.
Дифференцированное уравнение в операторной форме при нулевых начальных условиях имеет вид
![]() ,
,
откуда при Тср (р) = 1/р, получаем Тп(t) = 1-ехр (-t/τт)
Следовательно
температура датчика устанавливается
тем быстрее, чем меньше теплоемкость и
тепловое сопротивление. Теплоемкость
зависит от массы датчика, а следовательно
и от ее размеров. Как правило, с уменьшением
размеров теплоемкость уменьшается
быстрее, чем теплоотдача. Поэтому
быстродействующие датчики должны иметь
малые размеры. Так, в случае датчика в
виде длинного провода диаметром d,
охлаждаемого за счет вынужденной
конвекции, его объем , а значит и
теплоемкость пропорциональны квадрату
диаметра, а площадь поверхности- диаметру.
Как следует из (***), коэффициент теплоотдачи
пропорционален d-0,5,
таким образом, τт~d1,5
и при уменьшении диаметра вдвое тепловая
постоянная времени датчика уменьшается
в
![]() раза. Следует иметь в виду, что возможности
снижения т
за счет уменьшения размеров датчика
ограничены, т.к. при этом снижается
механическая прочность.
раза. Следует иметь в виду, что возможности
снижения т
за счет уменьшения размеров датчика
ограничены, т.к. при этом снижается
механическая прочность.
Наибольшее быстродействие имеют датчики в виде тонкой металлической пленки, нанесенной на тонкую диэлектрическую подложку и закрепленной на металлическом основании с хорошей теплоотдачей. Однако влияние на т путем уменьшения Rт эффективно лишь до конкретного предела. При хорошем теплоотводе температуру разных участков пленки уже нельзя считать одинаковой, так как верхние слои пленки реагируют на внешнее воздействие быстрее, чем внутреннее. В этом случае приходится усложнять математическую модель датчика, учитывая неравномерность температуры в разных его точках.
Уравнением (∆) можно удовлетворительно описать датчики простейшей конфигурации, например, в виде тонкой нити в воздушном потоке, термисторе в форме бусинки или термопары. Такие датчики имеют малые размеры и невысокую механическую прочность. Поэтому их снабжают защитными элементами. Одна из возможных конструкций датчика показана на рисунке.



















3 2 1. Здесь термопара со слоем 1 заключена в защитный металлический кожух 2, заполненным изолированным материалом 3, например, кварцевым песком или порошком оксида алюминия.




 При
такой конструкции приходится учитывать
два этапа теплообмена: между средой и
кожухом и кожухом и слоем термопары,
чему соответствует модель в виде двух
RC-
цепочек
При
такой конструкции приходится учитывать
два этапа теплообмена: между средой и
кожухом и кожухом и слоем термопары,
чему соответствует модель в виде двух
RC-
цепочек
R1 R2
C 1 C2
Здесь R1 характеризует тепловое сопротивление по поверхности кожуха;
R2- сопротивление воздушной прослойки между кожухом и термопарой
С1 и С2 определяют теплоемкости кожуха и термопары.
Для большинства быстродействующих преобразователей постоянная времени τт составляет доли секунды и ее существенное уменьшение ограничено условиями теплообмена и механической прочностью. Увеличение быстродействия достигают применением корректирующих устройств, к которым подводят сигнал датчика. Существуют различные методы построения таких устройств при воздействиях разного рода, например скачка температуры или ее монотонного изменения.
В качестве примера можно рассмотреть простейшую корректирующую RкСк- цепь, предназначенную для увеличения быстродействия термопары.
Rk







Ск
Rн


Пусть инерционные свойства термопары характеризуются постоянной времени τт.
Тогда термо ЭДС Ет=Ету/ (1+γωτт), где
Ету- установившееся значение термо ЭДС
Rн- сопротивление нагрузки.
Согласно рисунка
Rk
 Rt
Rt






Ивых
Rн


Ет
Ск
И
Выходное напряжение
![]()
где Rт – внутреннее сопротивление термопары
τк = RкСr
τт = RC
Выбрать τк= τт, получили
![]() ,
где
,
где
τ1= τ к (Rт+Rн) / (Rт+Rн+Rк)
Так как τк > τ1, то коррекция данного вида позволяет увеличить полосу пропускания устройств.
∆ω0,7 = 1/τ1 в (Rт+Rн)/(Rт+Rн+ Rк) раз.
При R <<Rн отношение τ1/ τ к Rн/(Rн Rк)
Положив, например, Rк = 9Rн , получим десятикратное увеличение полосы пропускания. Однако этому будет сопутствовать уменьшение коэффициента передачи Uвых/Ету в 10раз.
Таким образом, наряду с полезным коэффициентом – расширения полосы пропускания, следствием коррекции является увеличение влияния на результаты измерений наводок на цепь термопары. Рассмотренный метод коррекции позволяет получить расширение полосы пропускания на 1-2 порядка. Эффективность коррекции ограничена из-за приближенного характера моделирования термопары RС- цепью, не учитывающего нелинейность тепловых процессов, обусловленных зависимостью теплоемкости и теплового сопротивления от температуры.
Термометры расширения
Различают газовые, биметаллические, манометрические и жидкостные термометры. Их действия основано на тепловом расширении газов. Жидкостей и твердых тел.
Шкала МПТШ является термодинамической, поскольку характеризует среднюю кинетическую энергию движущихся молекул и атомов. Поэтому температуру можно определить, используя закон Клайперона
![]() ,
где
,
где
p и V- давление и объем идеального газа,
m – масса газа
μ – относительная молекулярная масса
R – 8,310 Дж/(моль.град.)- универс. газов. постоянная
Т – абсолютная температура
Термометры, работа которых основана на этом соотношении, называют газовыми. Возможно два варианта их построения:
при постоянном объеме газа или при его постоянной температуре.
В термометрах постоянного объема
![]() ,
где
,
где
Р и Ро – измеренное давление газа и его давление при температуре плавления льда То.
В термометрах постоянного давления
![]() ,
где
,
где
VиVо – объемы газа при измеряемой температуре и температуре плавления льда То.
Более точным является термометр постоянного объема.
5

 3
4
3
4
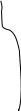


2




 6
6


1


Газ, содержащийся в рабочем резервуаре 1, через капилляр 2 поступает в пространство над уровнем ртути в коротком колене 3 ртутного манометра. Из верхней части 4 длинного колена манометра воздух предварительно откачивают (трубка не показана) Таким образом, давление газа определяют по шкале 5 как разность высот столбов в коленах манометра. При начальной температуре газа То с помощью поршня 6 устанавливают определенный начальный уровень ртути в коротком колене, соответствующий нулевой отметке шкалы 5. Этот уровень контролируется по шкале визуально или с помощью емкостного датчика уровня. По разности уровней в коленах определяют начальное давление Ро. При нагревании газа в резервуаре 1 ртуть вытесняется из короткого колена. Начальный уровень(начальный объем газа) восстанавливается смещением поршня в внизу. Этому положению соответствует большая разность уровня, отвечающая давлению Р1.
В показании прибора для повышения точности вводят ряд поправок, учитывающих:
а) изменения объема резервуара из-за температурного расширения его материала объема;
б) влияние слабо нагретого газа в капилляре и в коротком колене манометра;
в) влияние оттока тепла от резервуара по капилляру;
г) неоднородность нагрева газа.
Кроме того, вводится поправка на не идеальность газа, т.к. для реального газа
![]() ,
где
,
где
В и С- определяемые экспериментально коэффициенты.
Весь процесс измерений весьма трудоемок и требует большой тщательности. Поэтому подобные годовые термометры имеют весьма ограниченное применение и используется эталоне единицы температуры в диапазоне (13,8…273,15)К.
Термометры постоянного объема применяют в анализаторах состава газа. Анализируемый газ помещают в замкнутый объем и облучают короткими световыми импульсами с заданными спектральным составом. Если частота световой волны совпадает с линией поглощения одной компонент газа, то происходит его адиабатическое нагревание и приращение температуры оценивают по увеличению давления газа.
Дилатометрические термометры часто изготавливают в виде стержня, коаксиально закрепленного внутри цилиндра из материала с другим коэффициентом расширения. Длину стержня при температуре Т1 можно описать приближенной зависимостью
![]() ,
где
,
где
L0- начальная длина при температуре Т0;
L1 – коэффициент линейного расширения.
Если стержень и цилиндр выполнены из разных материалов с L1 и L2 соответственно, но с одинаковой начальной длиной L0, то разность длин Δ L при температуре Т1 будет равна
![]() ,
где
,
где
Разность Δ L пропорционально изменению температуры и ее измеряют по шкале, или каким- либо другим способом. Часто перемещения используют для управления контактами реле в системах регулирования температуры. Поскольку реально существуют температурные зависимости коэффициентов L1(T) и L2(T), то нелинейность градуированной характеристики тем больше, чем ниже диапазон измеряемых температур.
Дилатометрические термометры имеют исключительно простую конструкцию и высокую надежность. Промышленность выпускает такие термометры для нескольких диапазонов температур в интервале (-30…1000)о С с предельной погрешностью (1,5…2,5)%.
В биметаллическом термометре чувствительным элементом явился биметаллическая пластина, состоящая из двух слоев металлов обычно одинаковой толщины с разными коэффициентами линейного расширения. При нагревании такая пластина изгибается в сторону слоя с меньшим коэффициентом линейного расширения. Если один конец пластины длиной L и толщиной d закреплен, то перемещения Δ L свободного ненагруженного конца будет равно
![]() где
где
j- удельный изгиб пластины, зависящий от L1 и L2.
2

Д
1
3






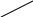


![]() Биметаллические
термометры при соответствующем подборе
металлов могут работать в диапазоне
температуры(-100…600)оС.
Их основная погрешность лежит пределах
(3-5)%. Недостатки их является необходимость
индивидуальной градуировки.
Биметаллические
термометры при соответствующем подборе
металлов могут работать в диапазоне
температуры(-100…600)оС.
Их основная погрешность лежит пределах
(3-5)%. Недостатки их является необходимость
индивидуальной градуировки.
Биметаллические датчики как дешевое и надежное устройство широко используется в бытовой технике и автомобилестроении.
Жидкостные термометры состоят из заполненного жидкостью баллона, соединенного с капилляром. С ростом температуры жидкость выжимается в капилляр, и по положению мениска судят о температуре. Баллон и капилляр обычно выполняют из стекла, поэтому такие термометры иногда называют стеклянными. В качестве термометрной жидкости чаще всего применяют ртуть, которая находится в жидкостном состоянии при температуре от –39О С до 357ОС. для более низких температур (-80…70)0С применяют подкрашенный этиловый спирт. Жидкостные термометры характеризуются высокой точностью, простотой и низкой стоимостью.
Основные недостатки жидкостных термометров хрупкость и невозможность передачи показаний на расстояние. Промышленность выпускает термометры для измерений температуры от –300С до 6000С. Основная погрешность составляет от 0,050С для термометров с узким диапазоном (4…5)0С измеряемых температур и до нескольких градусов в пределах от 0 до 4000С.
Для регулирования температуры выпускаются ртутные контактные термометры, в которых при достижении определенной температуры замыкается контакт между столбиком ртути и проводом, помещенным в капилляр.
Источниками погрешности служат процессы изменения свойств стекла со временем, взаимодействие мениска и стекла капилляра, внешнее давление среды.
В манометрических термометрах температуру оценивают по изменению давления газа или жидкости в замкнутом баллоне при изменении температуры. Поскольку жидкость практически несжимаемая, то в этом случае увеличение объема сопровождается резким увеличением давления. Манометрические термометры состоят из металлического термобаллона, соединенного с манометром с помощью капилляра. Длина последнего может составлять до десятков метров, что позволяет обеспечить дистанционность измерений.
Рассмотрим подробнее действие термометра с жидкостью. За счет увеличения температуры (Т1>Т0) относительное изменение объема цилиндрического резервуара V c диаметром d и длиной L составит
![]()
Объем жидкости при этом возрастет на
![]() ,
где
,
где
β- коэффициент объемного расширения.
Объем жидкости, вытесненный из баллона в манометр,
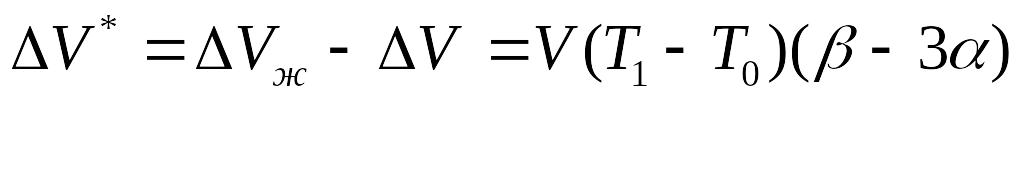
Эта жидкость охлаждается в капиллярах до начальной температуры Т0, при этом ее объем несколько уменьшается и составит
![]()
Таким образом, изменение объема полости манометрического устройства
![]()
Манометрические термометры выпускаются для температур от –200 до 6000С. При этом основная погрешность для большинства таких приборов равна (1,5…2,5)%. Длина капилляров составляет несколько метров, но может достигать 40м.
РЕЗИСТИВНЫЕ ПРЕОБРАЗОВАТЕЛИ
В резистивных преобразователях используют зависимость сопротивления резисторов от температуры. Разработанные специально для построения термометров резисторы называют терморезисторами, которые могут быть как из металла, так и из полупроводникового материала.
Для температурных измерений предпочтительно использовать металлы с линейной температурной зависимостью сопротивления, хорошей воспроизводимостью этой зависимости и устойчивостью к воздействию окружающей среды. В наибольшей степени этим требованиям удовлетворяет платина, но часто используют вольфрам, никель, медь и некоторые сплавы.
Сопротивление металлических терморезисторов, иногда называемых болометрами, возрастает с увеличением температуры. Градуировочная характеристика терморезистора зависит от применяемого металла и его чистоты, причем с ее ростом уменьшается температурная зависимость. Поэтому чистоту металла принято оценивать параметром
![]()
где R100 и R0 — сопротивления при температурах 100 °С и О °С.
Используемая для изготовления терморезисторов платина может иметь w100 = 1,3910 или 1,3850, для меди w100 = 1,4260 или 1,4280. По значению w100 можно рассчитать среднее значение ТКС в диапазоне температур (0.. .100) °С
![]() ,
,
откуда
ТКС
=10-2(w100
- 1). Для платиновых термометров среднее
значение ТКС
![]() .
.
Градуировочные характеристики терморезисторов нелинейные и для определенных диапазонов температур приводят аппроксимирующие поли номы. Так для платины с w100
![]()
![]()
![]()
![]()
Для медного терморезистора с w100 = 1,426 характеристика практически линейная
![]() (50...200)°С.
(50...200)°С.
Различают проволочные и пленочные терморезисторы. Проволочные изготавливают из проволоки диаметром (0,05...0,2) мм. Существует большое количество конструкций для разных условий эксплуатации. Например, в герметичной конструкции чувствительного элемента, показанной на рис. 1.6, спираль 1 из платинового провода размещена в цилиндрических каналах керамического каркаса 2, которые заполнены порошком оксида алюминия. Этот элемент помещают в защитный металлический кожух, снабженный арматурой для крепления, например, в виде фланца с разъемом.

Такие датчики предназначены для введения в канал с потоком газа или жидкости и называются погружаемыми. Их выпускают с сопротивлениями R = 1, 10, 50, 100, 500 Ом. Для измерений температуры поверхности предназначены терморезисторы в виде плоской спирали, имеющие хороший тепловой контакт с поверхностью. Погрешность измерений температуры прецизионными проволочными терморезисторами составляет до 10-3 °С в диапазоне температур (0...100) °С.
Пленочные терморезисторы образованы пленкой, нанесенной на диэлектрическую подложку. Например, выпускаются терморезисторы из платановой пленки, нанесенной с двух сторон на керамическую пластину толщиной (1...2) мм, шириной (0,1...0,2) мм и длиной (5... 10) мм. Для медицинских измерений используют пленочные платиновые терморезисторы разме-ром (0,1x0,3) мм. Полупроводниковые терморезисторы, часто называемые термисторами, широко применяются в измерительной технике. Их сопротивление аппроксимируют зависимостью
![]() ,
,
где А, В, С - коэффициенты; Т- температура в К.
Погрешность такой аппроксимации составляет не более (0,2...0,4) К в диапазоне температур (-60... 100)° С.
В узком диапазоне пользуются соотношением
![]() (1.12)
(1.12)
В зависимости от диапазона измеряемых температур значение коэффициента В несколько меняется, причем при высоких температурах В возрастает. Изменения 5 для разных термисторов может составлять от 10 до 50% от их максимального значения. Обычно в справочных данных приводят номинальное значение Кн при температуре Тн = 293 К (20 °С). В этом случае
 .
(1.13)
.
(1.13)
Для изготовления термисторов, как правило, используют кобальто-марганцевые (КМ), медно-марганцевые (ММ) и другие оксидные полупроводники. Существуют основные конструкции в виде стержней, дисков и бусинок размером в доли миллиметра из полупроводникового материала, защищенные от внешних воздействий металлическим кожухом или стеклянным баллоном. Так, стержневой термистор ММТ-4а заключен в металлический корпус 1 (рис. 1.7, а). Один вывод термистора осуществлен через проходной стеклянный изолятор 2, а второй соединен с корпусом. Термистор СТЗ-19 представляет собой бусинку 1 диаметром около 1 мм, защищенную стеклянным корпусом 2 (рис. 1.7, б). На корпусе укреплены выводы 3 диаметром 0.4 мм, соединенные с бусинкой тонкими проводами 4. Существуют прецизионные термисторы в виде покрытой слоем стекла бусинки с выводами из сплава платины с индием (рис. 1.7, в). Подобные термисторы характеризуются высокой стабильностью сопротивления.
Температурную чувствительность термистора оценивают его ТКС, определяемым при 20 °С,
![]() .
.
Для большинства
термисторов коэффициент В
![]()
![]() .
Тогда при
.
Тогда при
20 °С ТКС
![]() .
.

Рис. 1.7
Значения ТКС термисторов из разных материалов лежат в пределах от - 0,02 до - 0,08 К-1, что на порядок превышает ТКС металлических терморезисторов.
Существуют различные конструкции датчиков медицинского назначения, предназначенных для инвазивных и неинвазивных измерений. Один из типов датчика для инвазивных измерений (рис. 1.7, г) состоит из инъекционной иглы 1, в которой на диэлектрическом основании 2 закреплен бусинко-вый термистор 3.
Термисторам свойственна большая нелинейность зависимости Rт (T), что вызывает значительную погрешность.
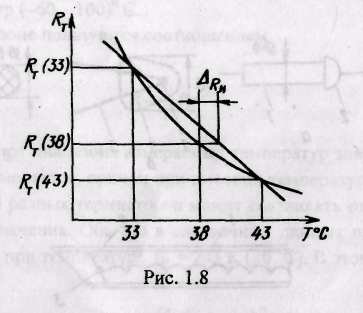
Пример 1.4. Рассмотрим медицинский термометр с диапазоном измерений (33...43) °С, выполненный на термисторе. В качестве аппроксимирующей линии примем прямую, которая пересекает кривую Rт (T) при Т =33 °С и 43°С (рис. 1.8).
Тогда погрешность
нелинейности
![]() можно оценить по разности температур,
соответствующих RT(38)
для линейной и нелинейной зависимостей.
Положим В
=3-103
К, RT(20)
= 3 кОм. Тогда на основании (1.13) получим
RT(33)
= 1942 Ом, Дт(38)
=1659 Ом, RT(43)=1424Ом.
можно оценить по разности температур,
соответствующих RT(38)
для линейной и нелинейной зависимостей.
Положим В
=3-103
К, RT(20)
= 3 кОм. Тогда на основании (1.13) получим
RT(33)
= 1942 Ом, Дт(38)
=1659 Ом, RT(43)=1424Ом.
Температура, соответствующая RT(38) при линейной характеристике,
![]()
Погрешность при линейной аппроксимации составляет = 38,5-38 = 0,5 °С, что чрезмерно велико для медицинских измерений. Полученное значение погрешности можно уменьшить приблизительно в два раза, если аппроксимирующая линия проведена так, что погрешности при Т= 33, 38 и 43°С одинаковы по модулю. Но и в этом случае погрешность линейной аппроксимации превышает 0,2°С, что также недопустимо для термометра медицинского назначения. Поэтому даже при малом диапазоне измеряемых температур приходится прибегать к линеаризации исходной зависимости RT(T).
Существует несколько методов линеаризации. Для случая питания термистора от генератора тока линеаризирующий резистор RЛ подключают параллельно термистору (рис. 1.9, а). Температурная зависимость сопротивления параллельной цепочки
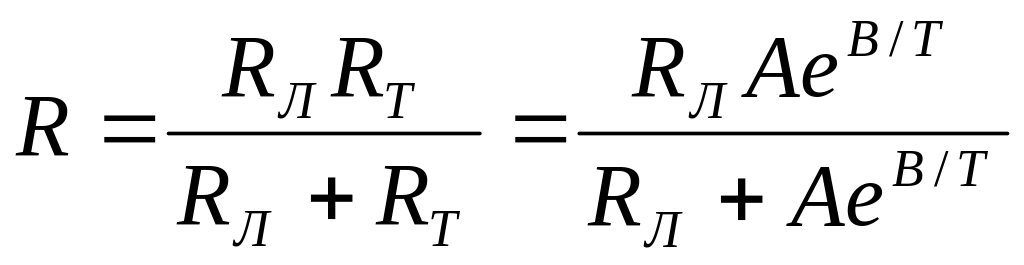
![]()
имеет вид S-образной
кривой. Линеаризация заключается в
подборе значения RЛ,
обеспечивающего параллельность кривых
R(Т)
и RT(T)
при заданной
температуре
![]() ,
(рис. 1.9, 6). Затем
к кривой в точке
,
проводят касательную (штриховая линия
на рисунке), которую и считают градуировочной
характеристикой цепочки.
,
(рис. 1.9, 6). Затем
к кривой в точке
,
проводят касательную (штриховая линия
на рисунке), которую и считают градуировочной
характеристикой цепочки.
Линеаризирующее сопротивление определяется по формуле
![]() (1.14)
(1.14)

Можно показать, что при В = 3000 К изменению температуры от номинальной на ±10 °С соответствует отклонение от линейности 0,03 С, а при изменении на ±15 °С - 0,15 °С. Линеаризация приводит к уменьшению чувствительности: температурный коэффициент сопротивления цепочки
![]() .
.
Существуют и другие методы линеаризации, например, на основе неуравновешенных мостов.
В измерительной схеме к терморезистору для измерения его сопротивления подводят некоторую мощность, при этом терморезистор разогревается по сравнению с телом, температуру которого измеряют, что приводит к погрешности. Это приращение можно рассчитать, если известна мощность и интенсивность теплообмена терморезистора с окружающей средой. На практике же в паспортных данных терморезисторов часто приводят значение минимальной мощности, при которой сопротивление находящегося в спокойном воздухе терморезистора изменяется на 1% от значения До- В зависимости от размеров терморезистора и его конструкции эта мощность лежит в пределах от долей до единиц мВт.
В процессе эксплуатации или хранения терморезисторов несколько изменяются их свойства. Так, на поверхности металлических терморезисторов появляется оксидная пленка, заметно меняющая (на сотые доли процента) сопротивление платиновых терморезисторов. Непостоянство R0 проволочных терморезисторов может быть вызвано изменяющимися внутренними напряжениями в спирали при циклическом изменении температуры.
Согласно требованиям стандартов изменение сопротивления термисто-
ров лежит в пределах до 3% и 30% при сроках хранения 18 месяцев и 10 лет соответственно. Однако фактически стабильность оказывается более высокой.
Нестабильность прецизионных термисторов в стеклянной оболочке может составлять до 0,2% в год, что соответствует погрешности измерений температуры 0,05 °С.
