
- •1. Задачи и объём проекта,
- •2. Буквенные обозначения основных величин
- •3. Объём работ
- •3.1. Структурный анализ плоских рычажных механизмов
- •3.3. Кине 3.3 Кинематическое исследование плоских рычажных механизмов
- •3.3.1. Построение планов механизма
- •3.3.2. Построение траекторий точек звеньев механизма
- •3.3.3. Определение скоростей и ускорений точек звеньев механизма
- •Угловое ускорение шатуна определяется с помощью уравнения
- •3.4. Силовой расчёт механизма
- •Значение кинематических параметров
- •3.4.1. Определение сил, действующих на звенья механизма
- •3.4.2. Определение реакций в кинематических парах
- •3.4.3. Определение уравновешивающего момента
- •Министерство транспорта российской федерации
- •Содержание 44 Барышников Сергей Олегович
3.4.1. Определение сил, действующих на звенья механизма
А.
Силы давления газов
![]() или
или
![]()
Во
всех заданиях на курсовое проектирование
эти силы даны в табличной форме в виде
зависимости давления газов в цилиндре
двигателя (компрессора) от положения
поршня. В соответствии с законом изменения
давления газа в цилиндре при перемещении
поршня строится рабочая (индикаторная)
диаграмма. Для двухтактных машин, в
которых рабочий процесс происходит за
два хода поршня (за 1 оборот кривошипа)
построение индикаторной диафрагмы
рекомендуется выполнять следующим
образом. На оси абсцисс откладывается
ход поршня (ползуна) из плана положений
механизма. На нём отмечаются точки,
соответствующие положениям ползуна
В1,
В2,
… , В3
(рис. 3). Ход ползуна
![]() разбивается на равные части в соответствии
с таблицей исходных данных для построения
индикаторной диаграммы. Для графического
отображения максимального давления
разбивается на равные части в соответствии
с таблицей исходных данных для построения
индикаторной диаграммы. Для графического
отображения максимального давления
![]() принимается отрезок
принимается отрезок
![]() Тогда масштабный коэффициент по оси
ординат будет равен
Тогда масштабный коэффициент по оси
ординат будет равен
![]()
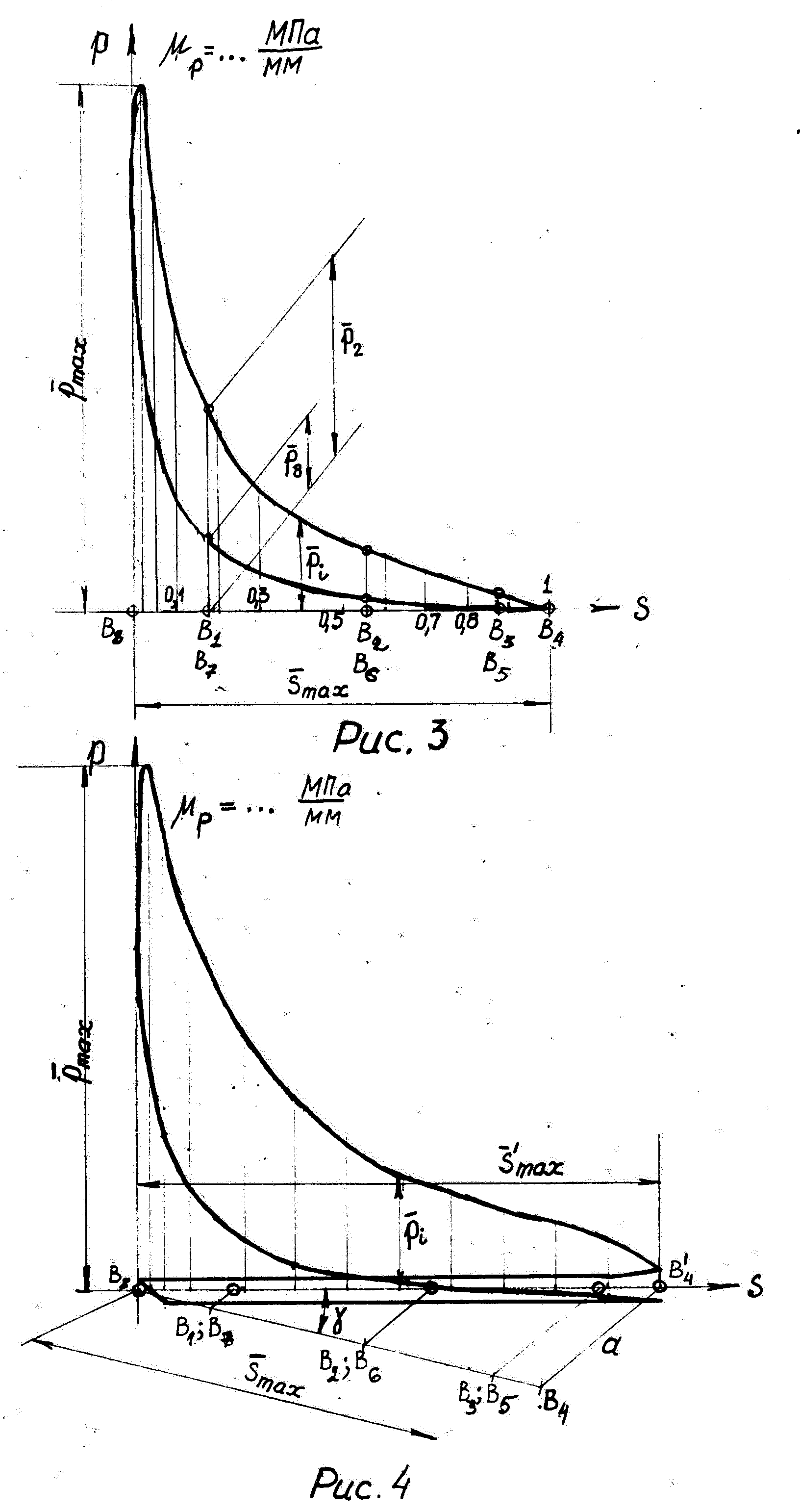 Для
четырёхтактных машин, в которых рабочий
процесс (рис. 4) происходит за четыре
хода поршня (за два оборота кривошипа),
по оси абсцисс предлагается отложить
отрезок
Для
четырёхтактных машин, в которых рабочий
процесс (рис. 4) происходит за четыре
хода поршня (за два оборота кривошипа),
по оси абсцисс предлагается отложить
отрезок
![]() Как и выше, максимальное давление
рекомендуется отображать отрезком
Как и выше, максимальное давление
рекомендуется отображать отрезком
![]() Чтобы определить на отрезке
Чтобы определить на отрезке
![]() точки, соответствующие местонахождениям
ползуна (т.е. точки В1,
В2,
…, В8),
воспользуемся известной из курса
математики теоремой Фалеса. С этой целью
под произвольным углом
точки, соответствующие местонахождениям
ползуна (т.е. точки В1,
В2,
…, В8),
воспользуемся известной из курса
математики теоремой Фалеса. С этой целью
под произвольным углом
![]() к оси абсцисс проводим из начала координат
полупрямую, на которой откладываем ход
ползуна
к оси абсцисс проводим из начала координат
полупрямую, на которой откладываем ход
ползуна
![]() из планов механизма (вместе с точками,
соответствующими всем положениям
ползуна). Через точки
из планов механизма (вместе с точками,
соответствующими всем положениям
ползуна). Через точки
![]() проведём отрезок а
. Отрезки,
параллельные а
и проходящие
через точки В1,
В2,
…, В3,
пересекут
ось абсцисс в искомых точках.
проведём отрезок а
. Отрезки,
параллельные а
и проходящие
через точки В1,
В2,
…, В3,
пересекут
ось абсцисс в искомых точках.
Индикаторную диаграмму следует изобразить в левом верхнем углу второго листа курсового проекта (построение снабжается надписью «ИНДИКАТОРНАЯ ДИАГРАММА»).
Очевидно, что сила,
с которой газы действуют на ползун в
его i-м положении, можно определить
следующим образом:
![]() где
где
![]() - площадь поршня (цилиндра), причём
- площадь поршня (цилиндра), причём
![]()
Б. Сила тяжести
![]()
Сила тяжести и положения центра тяжести каждого звена известны из задания (считаем, что центр тяжести и центр масс звена совпадают). Центр тяжести кривошипа принимается расположенным на оси вращения, а центр тяжести ползуна (поршня) – в центре шарнира, соединяющего это звено с соседним (т.е. с шатуном). В ряде заданий силы тяжести определяются по заданной массе звена и ускорению свободного падения:
![]()
где
![]() - масса
- масса
![]() го
звена, кг.
го
звена, кг.
В. Силы инерции
![]() и моменты сил инерции
и моменты сил инерции
![]()
Инерционные воздействия на звенья механизма возникают при неравномерном поступательном или вращательном движении звеньев, т.е. инерционные воздействия являются динамическими реакциями на вызываемые внешними силами ускорения . Это положение устанавливается и принципом Даламбера, на основании которого можно рассматривать систему как статическую, если к внешним силам добавить реактивные силы инерции.
Для тела, совершающего плоское движение (например, шатун), различают:
Главный вектор сил инерции звена, приложенный в центре масс и определяемый формулой:

Главный момент сил инерции звена, значение и направление которого определяется формулой:

В
двух последних формулах
- масса
![]() -
го звена, кг;
-
го звена, кг;
![]() - ускорение центра масс
-
го звена, м/с
- ускорение центра масс
-
го звена, м/с![]()
![]() - угловое ускорение
-
го звена, рад/с
- угловое ускорение
-
го звена, рад/с
![]() - момент инерции ускорение
-
го звена относительно главной центральной
оси, проходящей через центр масс, кг/м
- момент инерции ускорение
-
го звена относительно главной центральной
оси, проходящей через центр масс, кг/м![]()
При
поступательном движении звена (например,
ползун) равнодействующая сил инерции
![]() прикладывается к центру масс этого
звена.
прикладывается к центру масс этого
звена.
При вращательном движении с постоянной угловой скоростью (например, кривошип):
1). Если
центр масс S совмещён
с осью вращения звена (расстояние между
центром масс и осью вращения
![]() ),
силы инерции элементарных масс взаимно
уравновешиваются и равнодействующая
сил инерции
),
силы инерции элементарных масс взаимно
уравновешиваются и равнодействующая
сил инерции
![]()
2). Если
центр масс S звена не
совпадает с его осью вращения
![]() ,
получим силу инерции, приложенную в
центре масс, равную нормальной
(центробежной) силе инерции, направленной
от оси вращения:
,
получим силу инерции, приложенную в
центре масс, равную нормальной
(центробежной) силе инерции, направленной
от оси вращения:
![]()
Очевидно,
что в первом и во втором случаях главный
момент сил инерции звена
![]() (т.к.
(т.к.
![]() ).
).
При
вращательном движении с переменной
угловой скоростью
![]()
1). Если
![]() то
то
![]()
![]() ,
где
,
где
![]() - момент инерции звена относительно его
оси вращения;
- момент инерции звена относительно его
оси вращения;
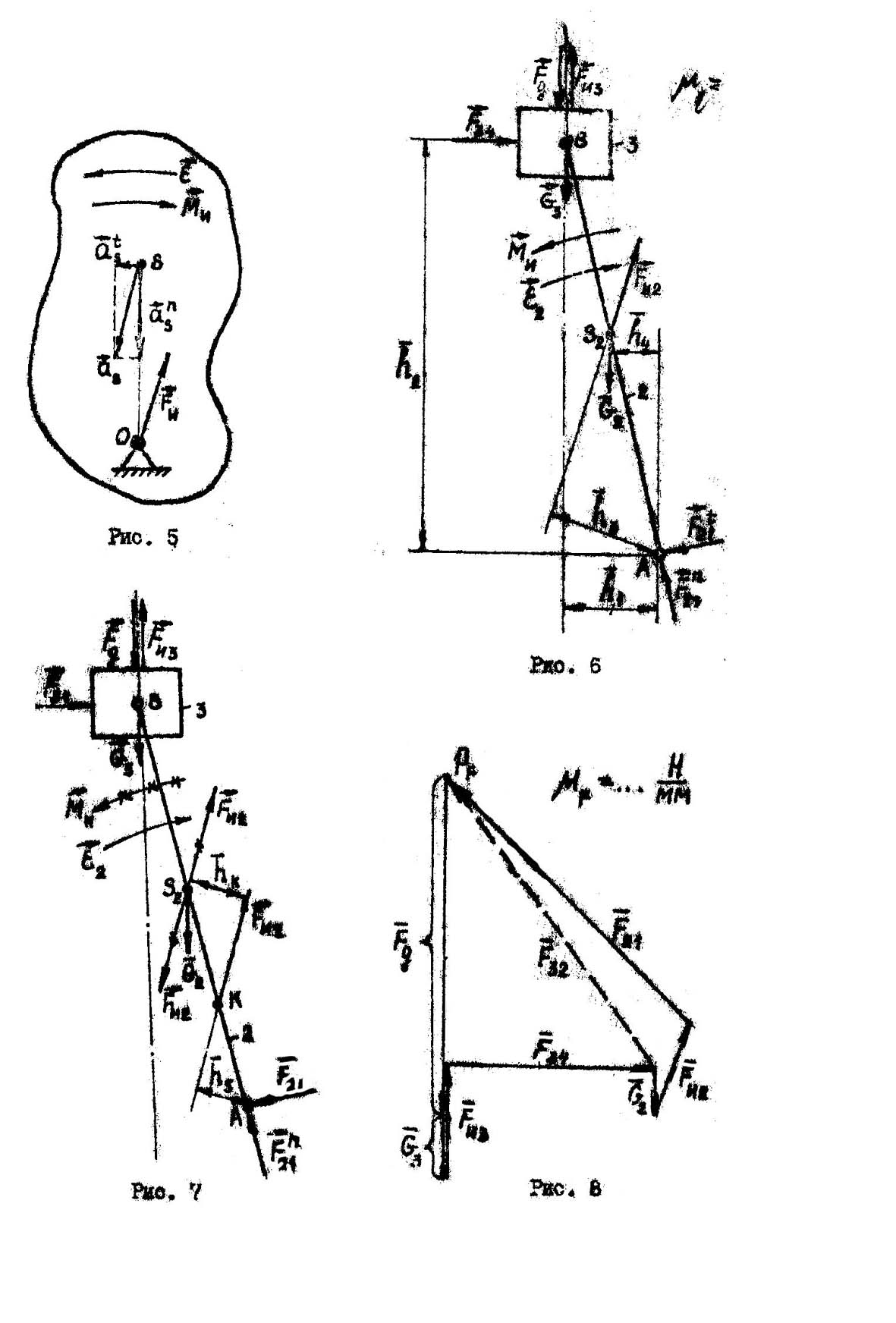 2).
Если
2).
Если
![]()
![]() (где
(где
![]() - полное ускорение центра масс звена),
- полное ускорение центра масс звена),
![]() (см. рис. 5).
(см. рис. 5).
Как
известно из курса теоретической механики,
полное ускорение центра масс звена
![]() Отметим, что сила
действует на шарнир 0.
Отметим, что сила
действует на шарнир 0.
