27. Ступенчатый вид матрицы,вид Гаусса

Матрица   имеет ступенчатый вид, если:

1. Все нулевые строки матрицы   стоят последними;

2. Для любой ненулевой строки матрицы   (пусть для определённости её номер равен  ) справедливо следующее: если 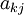  — первый ненулевой элемент строки  , то  .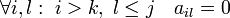

 Матрица считается матрицей ступенчатого вида по строкам если

• все ненулевые строки (имеющие по крайней мере один ненулевой элемент) располагаются над всеми чисто нулевыми строками;

• ведущий элемент (первый ненулевой элемент строки при отсчёте слева направо) каждой ненулевой строки располагается строго правее ведущего элемента в строке, расположенной выше данной.

Метод Гаусса: Ме́тод Га́усса— классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные^.

28. Ранг матрицы,его свойства

Количество линейно независимых строк матрицы называют строчным рангом матрицы, а количество линейно независимых столбцов матрицы называют столбцовым рангом матрицы. В действительности, оба ранга совпадают. Их общее значение и называется рангом матрицы.

Другой эквивалентный данному подход заключается в определении ранга матрицы, как максимального порядка отличного от нуля минора матрицы.

Свойства: Сложение и вычитание допускается только для матриц одинакового размера.

Существует нулевая матрица такая, что её прибавление к другой матрице A не изменяет A, то есть

Все элементы нулевой матрицы равны нулю.

Возводить в степень можно только квадратные матрицы.

• Ассоциативность сложения: 

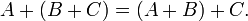
• Коммутативность сложения: 

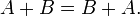
• Ассоциативность умножения: 

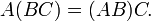
• Вообще говоря, умножение матриц некоммутативно: 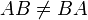 . Используя это свойство, вводят коммутатор матриц.

• Дистрибутивность умножения относительно сложения:

• С учётом упомянутых выше свойств, матрицы образуют кольцо относительно операций сложения и умножения.

• Свойства операции транспонирования матриц:

, если обратная матрица   существует.

29. Определитель матрицы,его свойства

 Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). Определитель матрицы А обозначается как: det(A), |А| или Δ(A).