25. Операции над матрицами

Умножение матрицы   на число   (обозначение:  ) заключается в построении матрицы  , элементы которой получены путём умножения каждого элемента матрицы   на это число, то есть каждый элемент матрицы   равен

Свойства умножения матриц на число:

• 1. 1A = A;

• 2. (λβ)A = λ(βA)

• 3. (λ+β)A = λA + βA

• 4. λ(A+B) = λA + λB

Сложение матриц   есть операция нахождения матрицы  , все элементы которой равны попарной сумме всех соответствующих элементов матриц   и  , то есть каждый элемент матрицы   равен

Свойства сложения матриц:

• 1.коммутативность: A+B = B+A;

• 2.ассоциативность: (A+B)+C =A+(B+C);

• 3.сложение с нулевой матрицей: A + Θ = A;

• 4.существование противоположной матрицы: A + (-A) = Θ;

Умножение матриц (обозначение:  , реже со знаком умножения  ) — есть операция вычисления матрицы  , элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго.

Количество столбцов в матрице   должно совпадать с количеством строк в матрице  , иными словами, матрица   обязана бытьсогласованной с матрицей  . Если матрица   имеет размерность  ,   —  , то размерность их произведения   есть  .

Свойства умножения матриц:

• 1.ассоциативность (AB)C = A(BC);

• 2.некоммутативность (в общем случае): AB   BA;

• 3.произведение коммутативно в случае умножения с единичной матрицей: AI = IA;

• 4.дистрибутивность: (A+B)C = AC + BC, A(B+C) = AB + AC;

• 5.ассоциативность и коммутативность относительно умножения на число: (λA)B = λ(AB) = A(λB)

Умножение вектора на матрицу

По обычным правилам матричного умножения осуществляется умножение на матрицу слева вектора-столбца, а также умножение вектора-строки на матрицу справа. Поскольку элементы вектора-столбца или вектора-строки можно записать (что обычно и делается), используя один, а не два индекса, это умножение можно записать так:

для вектора-столбца v (получая новый вектор-столбец Av):

для вектора-строки s (получая новый вектор-строку sA):

Вектор-строка, матрица и вектор столбец могут быть умножены друг на друга, давая число (скаляр):

(Порядок важен: вектор-строка слева, вектор-столбец справа от матрицы).

26. Элементарные преобразования матрицы

Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.

Элементарными преобразованиями строк называют:

• перестановка местами любых двух строк матрицы;

• умножение любой строки матрицы на константу  ,  ;

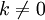• прибавление к любой строке матрицы другой строки.

В некоторых курсах линейной алгебры перестановка строк матрицы не выделяется в отдельное элементарное преобразование в силу того, что перестановку местами любых двух строк матрицы можно получить, используя умножение любой строки матрицы на константу  ,   и прибавление к любой строке матрицы другой строки, умноженной на константу  ,  .

Аналогично определяются элементарные преобразования столбцов.

Элементарные преобразования обратимы. Обозначение   указывает на то, что матрица   может быть получена из   путём элементарных преобразований (или наоборот)