20. Операции над комплексными числами.Заданными в тригонометр. Форме Тригонометрическая и показательная формы

Если вещественную   и мнимую   части комплексного числа выразить через модуль   и аргумент   ( ,  ), то всякое комплексное число  , кроме нуля, можно записать в тригонометрической форме

Также может быть полезна показательная форма записи комплексных чисел, тесно связанная с тригонометрической через формулу Эйлера:

где   — расширение экспоненты для случая комплексного показателя степени.

Отсюда вытекают следующие широко используемые равенства:

21. Извлечение корня из комплексного числа

Эта формула позволяет возводить в целую степень ненулевое комплексное число, представленное в тригонометрической форме. Формула Муавра имеет вид:

где   — модуль, а   — аргумент комплексного числа. В современной символике она опубликована Эйлером в 1722 году. Приведенная формуле справедлива при любом целом n, не обязательно положительном.

Аналогичная формула применима также и при вычислении корней  -ой степени из ненулевого комплексного числа:

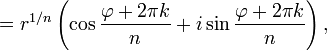
Отметим, что корни  -й степени из ненулевого комплексного числа всегда существуют, и их количество равно  . На комплексной плоскости, как видно из формулы, все эти корни являются вершинами правильного  -угольника, вписанного в окружность радиуса   с центром в начале координат.

22. Разложения многочлена на множители, основная теорема алгебры

Основна́я теоре́ма а́лгебры утверждает, что

Всякий отличный от константы многочлен (от одной переменной) с комплексными коэффициентами имеет по крайней мере один корень в поле комплексных чисел.

Теорема. Любой многочлен степени n вида   представляется произведением постоянного множителя при старшей степени   и n линейных множителей  , i=1, 2, …, n, то есть  , причем  , i=1, 2, …, n являются корнями многочлена.

Теорема Безу. При делении многочлена   на (x-s) получается остаток, равный значению многочлена в точке s, то есть  , где   - многочлен степени n-1.

23. Разложение рациональной дроби на сумму простейших дробей

Дробь, знаменателем которой является многочлен, может быть разложена следующим образом:

24. Виды матриц

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексныхчисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы.

Виды:

Транспонированная матрица

С каждой матрицей   размера   связана матрица   размера   вида

Такая матрица называется транспонированной матрицей для   и обозначается так  .

Транспонированную матрицу можно получить, поменяв строки и столбцы матрицы местами. Матрица   размера   при этом преобразовании станет матрицей размерностью   .

Диагональная матрица

Диагональная матрица — квадратная матрица, все элементы которой кроме диагональных — нулевые  , иногда записывается как:

Единичная матрица

Единичная матрица — матрица, при умножении на которую любая матрица (или вектор) остается неизменной, является диагональной матрицей с единичными (всеми) диагональными элементами:

Для ее обозначения чаще всего используется обозначение I или E, а также просто 1 (или 1 специальным шрифтом).

Для обозначения ее элементов также используется символ Кронекера  , определяемый как:

 при 

Нулевая матрица

Для обозначения нулевой матрицы — матрицы, все элементы которой нули (при сложении ее с любой матрицей та остается неизменной, а при умножении на любую получается нулевая матрица) — используется обычно просто 0 или 0 специальным шрифтом, или буква, начертанием похожая на ноль, например  .

Вектор-строка и вектор-столбец

Матрицы размера   и   являются элементами пространств   и   соответственно:

• матрица размера   называется вектор-столбцом и имеет специальное обозначение:

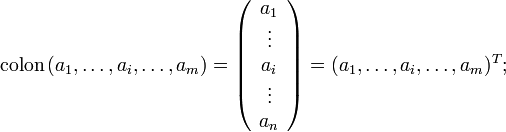
• матрица размера   называется вектор-строкой и имеет специальное обозначение: