16. Эллипс, ее свойства,каноническое уравнение

Каноническое уравнение:

Эллипс- геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний до двух данных точек и (называемых фокусами) постоянна и больше расстояния между фокусами, то есть причем

Свойства:

Если и — фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой 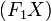равен углу между этой касательной и прямой .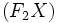
Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.
Эволютой эллипса является астроида.
Точки пересечения эллипса с осями являются его вершинами.
Эксцентриситет эллипса равен отношению 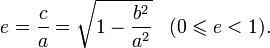Эксцентриситет характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.
Эллипс также можно описать как
- фигуру, которую можно получить из окружности, применяя аффинное преобразование
- ортогональную проекцию окружности на плоскость.
- Пересечение плоскости и кругового цилиндраа

17. Парабола, ее свойства,каноническое уравнение

Пара́бола — геометрическое место точек, равноудалённых от данной прямой(называемой директрисой параболы) и данной точки (называемой фокусом параболы).

Каноническое уравнение параболы в прямоугольной системе координат:

(или , если поменять местами оси)

Свойства:

Длина линий F-Pn-Qn одинакова. Можно сказать, что, в отличие от эллипса, второй фокус у параболы — в бесконечности (см. также Шары Данделена)

Парабола — кривая второго порядка.
Она имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и вершину перпендикулярно директрисе.
Оптическое свойство. Пучок лучей, параллельных оси параболы, отражаясь в параболе, собирается в её фокусе. И наоборот, свет от источника, находящегося в фокусе, отражается параболой в пучок параллельных её оси лучей.
Если фокус параболы отразить относительно касательной, то его образ будет лежать на директрисе.
Парабола является антиподерой прямой.
Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб.

18. Гипербола, ее свойства,каноническое уравнение

Гипе́рбола— геометрическое место точек M Евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух выделенных точек и (называемых фокусами) постоянно. Точнее,

причем