8. Вычисление смешанного произведения векторов,заданных своими координатами

Проще всего смешанное произведение находится, когда известны координаты векторов. Для вычисления используется формула  .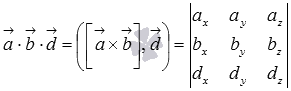

9. Уравнение прямой,проходящей через две точки: а)на плоскости б)в пространстве

а) Уравнение прямой, проходящей через две точки на плоскости: A(x₁, y₁) и B(x₂, y₂)

б) Пусть в пространстве заданы две точки M ₁ ( x ₁ , y ₁ , z ₁ ) и M₂ ( x ₂, y ₂ , z ₂ ), тогда уравнение прямой, проходящей через эти точки:

Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.На плоскости записанное выше уравнение прямой упрощается:

если х ₁ ≠ х₂ и х = х ₁ , если х ₁ = х₂

10. Общее уравнение прямой на плоскости, его частные случаи

Общее уравнение Ax + By + C (  > 0)

 Частные случаи:

     1) By + C = 0 - прямая параллельна оси Ox;

     2) Ax + C = 0 - прямая параллельна оси Oy;

     3) Ax + By = 0 - прямая проходит через начало координат;

     4) y = 0 - ось Ox;

     5) x = 0 - ось Oy

11. Угол между двумя прямыми на плоскости: условия параллельности и перпендикулярности двух прямых

Определение. Углом между прямыми в пространстве называют любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.

Условия параллельности: Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов  .

Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны:

 – условие параллельности прямых.

Условие перпендикулярности: Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю:

 – условие перпендикулярности прямых.

12. Общее уравнение плоскости, его частные случаи

  Общее уравнение плоскости 

где   - нормальный вектор плоскости.

Частные случаи общего уравнения плоскости:

     1) By + Cz + D = 0 - параллельна оси Ox;

     2) Ax + Cz + D = 0 - параллельна оси Oy;

     3) Ax + By + D = 0 - параллельна оси Oz;

     4) Cz + D = 0 - параллельна оси Oxy;

     5) By + D = 0 - параллельна оси Oxz;

     6) Ax + D = 0 - параллельна оси Oyz;

     7) Ax + By + Cz = 0 - проходит через начало координат;

     8) By + Cz = 0 - проходит через ось Ox;

     9) Ax + Cz = 0 - проходит через ось Oy;

     10) Ax + By = 0 - проходит через ось Oz;

     11) z = 0 - плоскость Oxy;

     12) y = 0 - плоскость Oxz;

     13) x = 0 - плоскость Oyz

13. Уравнение плоскости,проходящее через 3 заданные точки

Пусть даны три точки M₀(x₀ , y₀, z₀), M₁(x₁, y₁, z₁), M₂(x₂, y₂, z₂), которые лежат в одной плоскости. Пусть М (x, y, z) произвольная точка этой плоскости. Тогда векторы M₀M, M₀M₁, M₀M₂ лежат в одной плоскости и их смешанное произведение равно нулю: M₀M×(M₀M₁·M₀M₂) = 0

Расписывая смешанные произведения в координатной форме, получим: