Коллоквиум по линейной алгебре

1. Линейные операции над векторами,их свойства:

Существует несколько линейнх операций над векторами:

1.сложение/вычетание 2.умножение/деление векторов 3.умножение на число.

Сложение-есть параллельный перенос вектора- перемещение всех точек пространства в одном направлении на одинаковое расстояние. Сумма векторов а+b=с. Докажем: Приложим вектор   к некоторой точке  , получим  . Приложим вектор   к точке  , получим  . Тогда вектор   будем называть суммой векторов:  .

Докажем, что данное определение не зависит от выбора точки  . Приложим вектор   к другой точке  , получим  . Приложим вектор   к точке  , получим  .Рассмотрим направленные отрезки   и  . Они, очевидно, равны (см. рис.), поскольку   — параллелограмм.

Произведением вектора   на число   называется вектор, который:

1. коллинеарен вектору  ;

2. сонаправлен ему, если 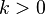 , или противоположнонаправлен, если  ;

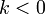3. длины связаны следующим соотношением:  .

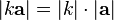Данное определение согласовано с определением сложения:

для любого натурального  .

Сложение векторов коммутативно:  .

Сложение векторов ассоциативно:  .

Прибавление нулевого вектора к любому не меняет последнего:  . Очевидно,  .

Для любого вектора   существует вектор   такой, что   или  .

Умножение вектора на число ассоциативно:  .

Умножение вектора на число дистрибутивно относительно сложения чисел:  .

Доказательство сводится к перечислению всех возможных знаков   и  , в каждом случае утверждение очевидно.Дистрибутивность умножения векторов относительно сложения

Умножение вектора на число дистрибутивно относительно сложения векторов:  . Это следует из подобия треугольников   и   на рисунке.

Очевидно, умножение на единицу не меняет вектор:  .

Геометрический смысл линейной зависимости заключается в следующем:

1. система из двух векторов линейно зависима тогда и только тогда, когда векторы коллинеарны;

2. система из трех векторов линейно зависима тогда и только тогда, когда векторы компланарны;

3. всякие четыре вектора линейно зависимы.

2. Скалярное произведение

Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на cos угла междуними.Обозначается ab,а* b(или( а, b)).Итак, по определению,  скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.

 1. Скалярное произведение обладает переместительным свойством: ab=ba

  

5. Если векторы а и b(ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если a b, то ab=0. Справедливо и обратное утверждение: если ab=0 и а 0b, то а b

.

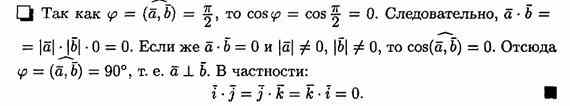
4. Выражение скалярного произведения векторов,заданных координатами

Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов   и  .

 В прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид ,

Доказательство:

Сначала докажем равенства 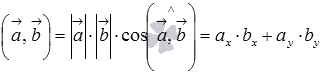  для векторов   на плоскости, заданных в прямоугольной декартовой системе координат. Будем считать точки О, А и В вершинами треугольника ОАВ. По теореме косинусов мы можем записать  . Так как  , то последнее равенство можно переписать как  , а по первому определению скалярного произведения имеем  , откуда  .

Вспомнив формулу вычисления длины вектора по координатам, получаем

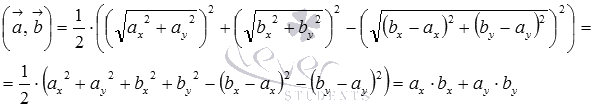
4. Вектороное произведение двух векторов и его свойства

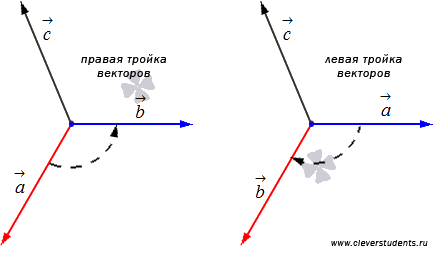
Отложим векторы   от одной точки. В зависимости от направления вектора   тройка   может быть правой или левой.

Векторным произведением двух векторов   и  , заданных в прямоугольной системе координат трехмерного пространства, называется такой вектор  , что

• он является нулевым, если векторы   и   коллинеарны;

• он перпендикулярен и вектору   и вектору   ( );

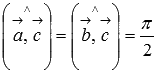• его длина равна произведению длин векторов   и   на синус угла между ними ( );

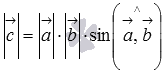• тройка векторов   ориентирована так же, как и заданная система координат.