9. Функції попиту на ресурси та пропозиції випуску.

Повернемось до моделі максимізації прибутку (3.1) і розглянемо ситуацію, коли ціна на продукцію може змінюватись на відрізку , а вектор цін на виробничі ресурси Тоді маємо справу зі сім’єю задач

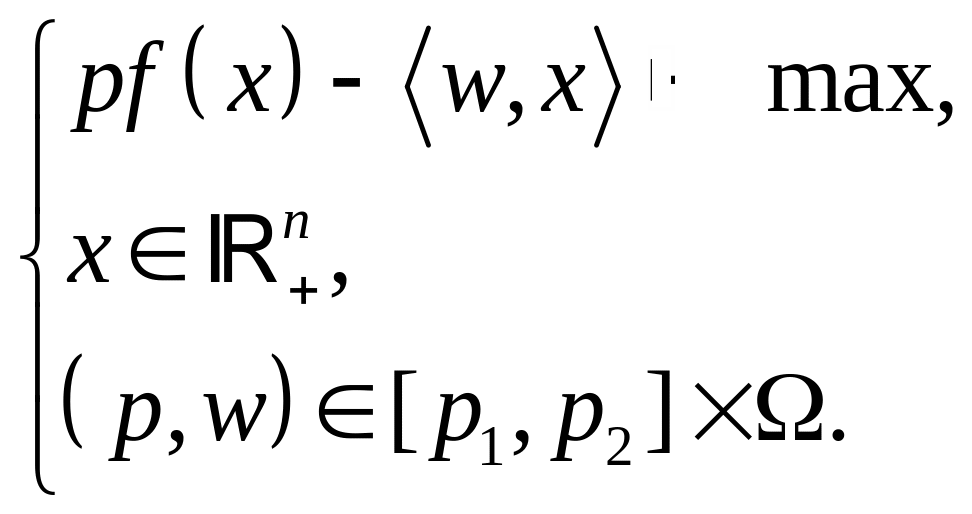(3.7)

Нехай

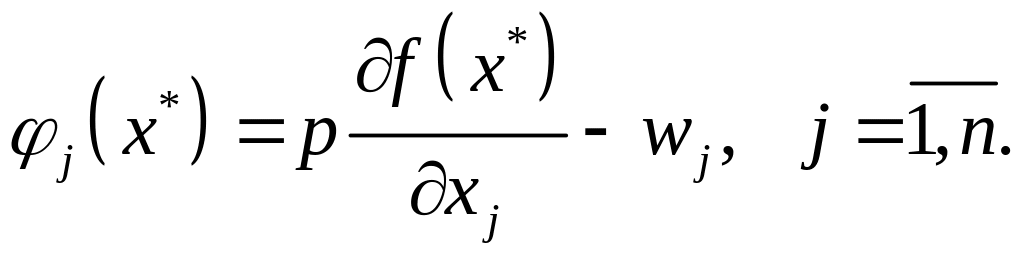
Згідно з умовами оптимальності (3.2) і (3.3) при , маємо:

(3.8)

Щоб розв’язати систему (3.8) відносно вектора оптимальних витрат , який залежить від параметрів та , потрібно, щоб матриця Якобі

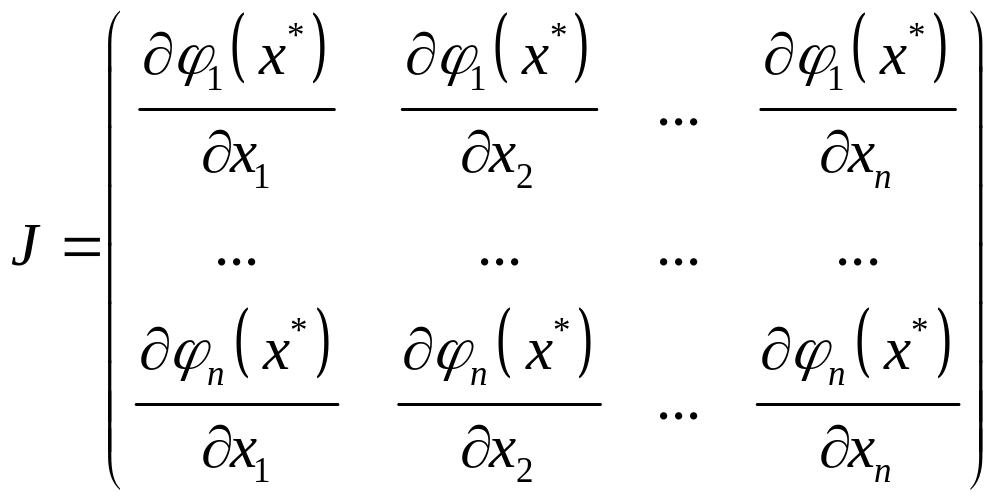
була невиродженою .

Оскільки в нашому випадку

а матриця Гессе вважається від’ємно визначеною (тобто ), то систему (3.8) справді можна розв’язати відносно . Вектор-функція

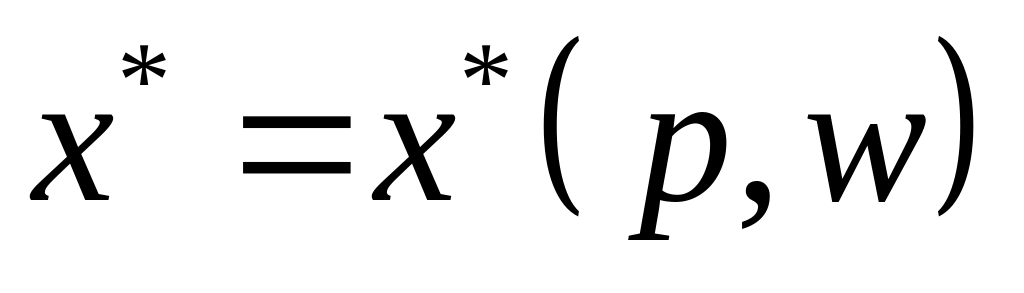(3.9)

є додатно однорідною нульового степеня, тобто

для всіх

Підставляючи у виробничу функцію , отримаємо залежність випуску від цін та , тобто

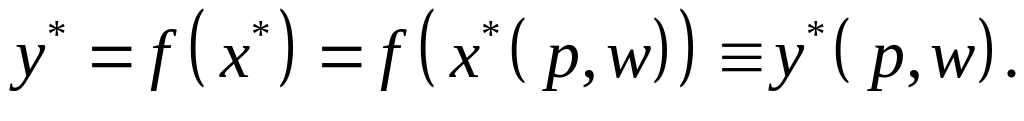(3.10)

Функція (3.10) (як і (3.9)) також є додатно однорідною нульового степеня:

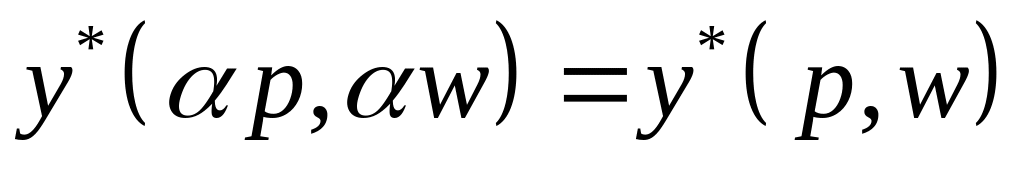для всіх

Означення 3.1. Визначені на множині функції та називаються відповідно функціями попиту на витрати та пропозиції випуску.

Властивості однорідності функцій попиту та пропозиції дозволяють зробити висновок про те, що пропорційні зміни в цінах продукції та факторів виробництва не впливають на витрати факторів та випуск продукції.

10. Порівняльна статика фірми. Основне матричне рівняння теорії фірми.

Рівняння реакції виробника на зміну ціни випуску.

Як і раніше, розглянемо сукупність задач (3.7). Умови оптимальності Куна-Таккера (3.3) та невиродженість матриці Якобі дозволяють розв’язати систему (3.3) і отримати в кінцевому результаті функції та . З урахуванням цього матимемо систему співвідношень:

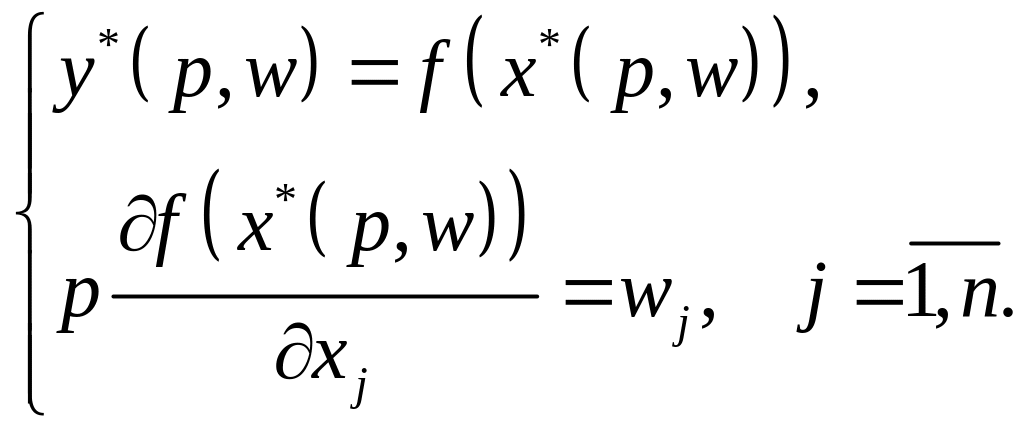(3.11)

Продиференціюємо (3.11) по :

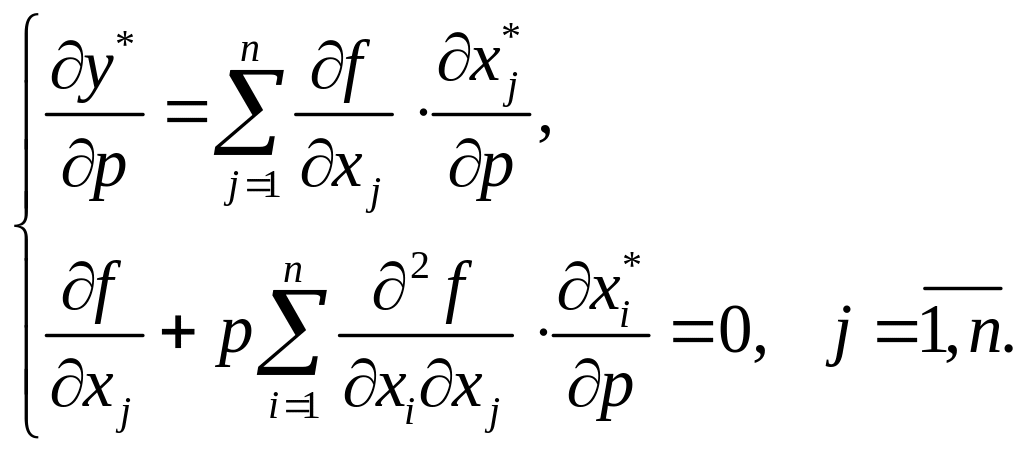(3.12)

В матрично-векторній формі система (3.12) перепишеться так:

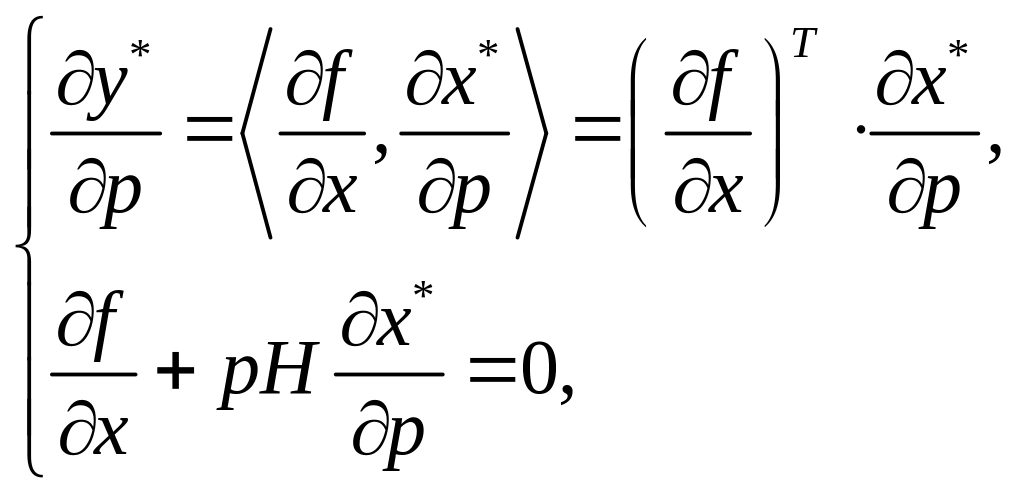
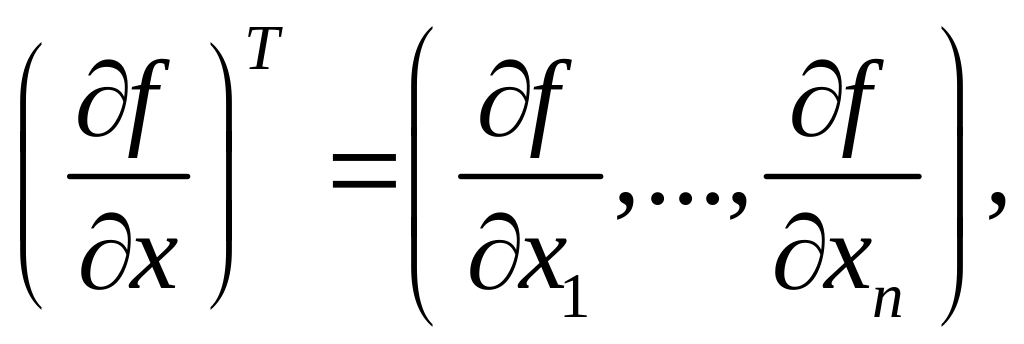
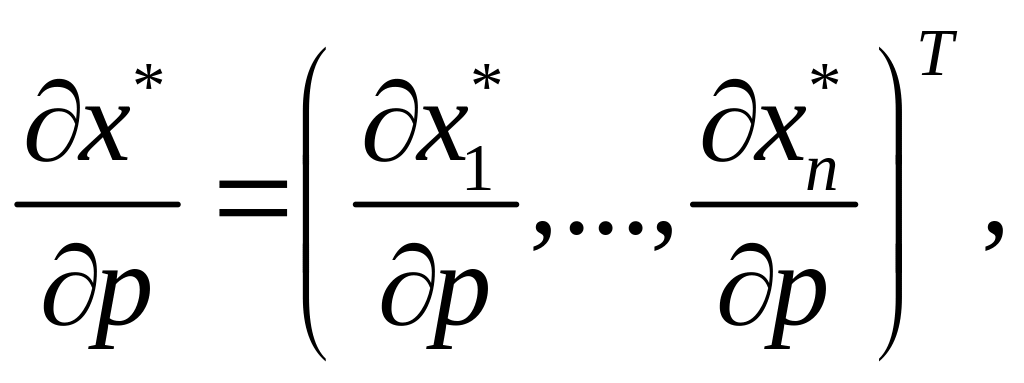
де – вектор-стовпець, – матриця Гессе. Однак надалі ця система буде використовуватись у формі

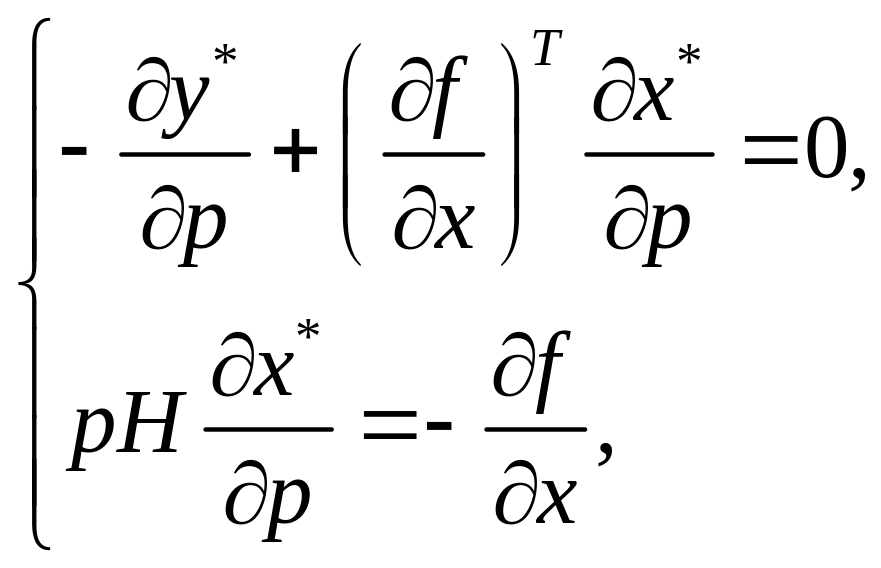(3.13)

де – скаляр.

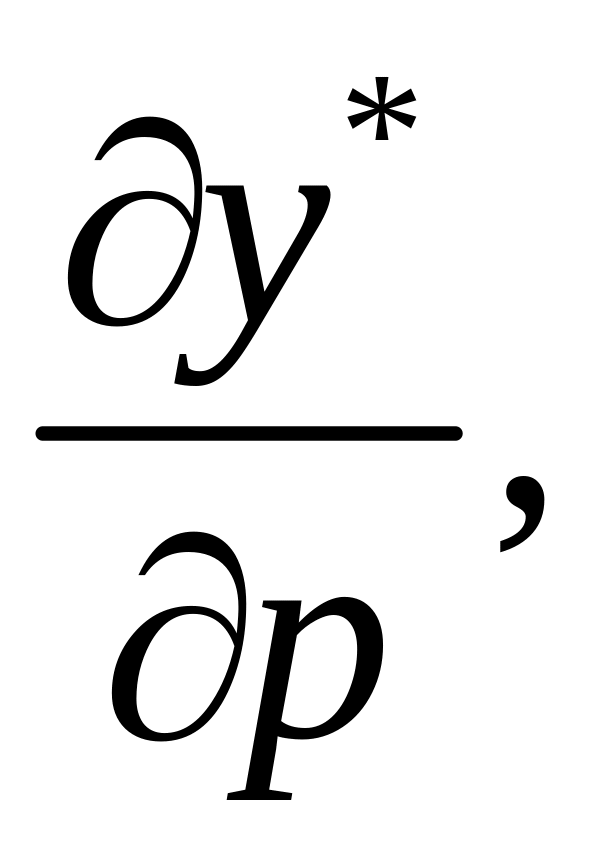
Система (3.13) (чи (3.12)) є системою відносно невідомих ( 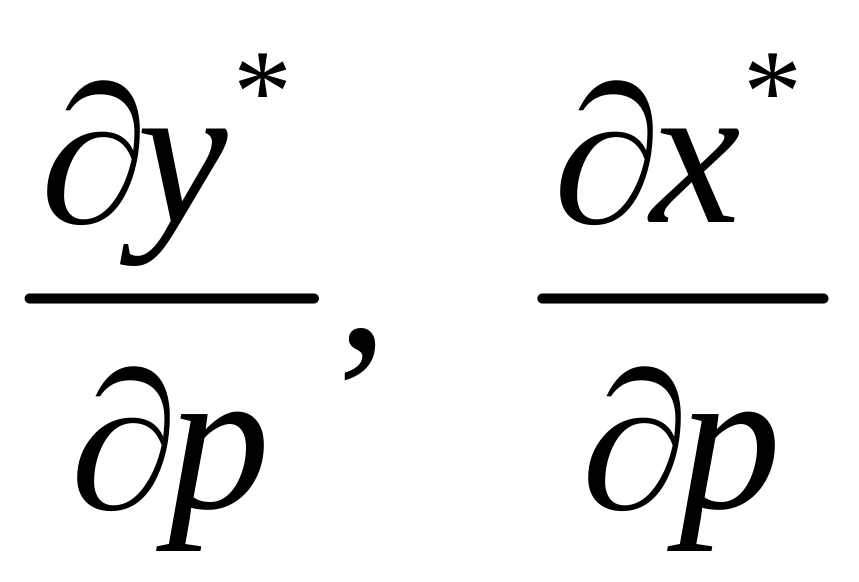– характеристики впливу зміни ціни випуску відповідно на оптимальний обсяг випуску та оптимальні витрати ресурсів). Для подальших викладень нам буде потрібна наступна форма (3.13):

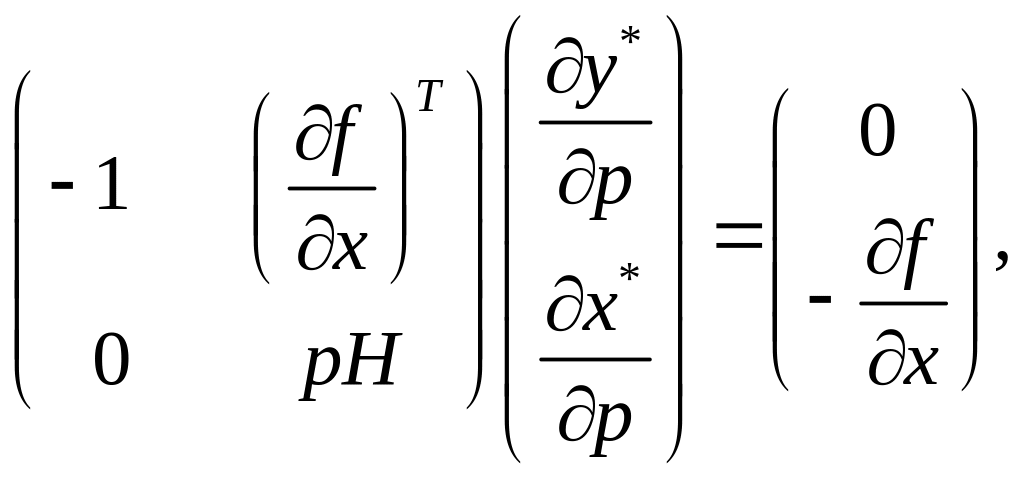(3.14)

де у лівій частині – вектор-стовпець, а у правій є скалярною величиною.

Рівняння (3.14) відображає реакцію виробника на зміну ціни випуску . Скориставшись правилом обертання блочних матриць, переконаємось, що

,

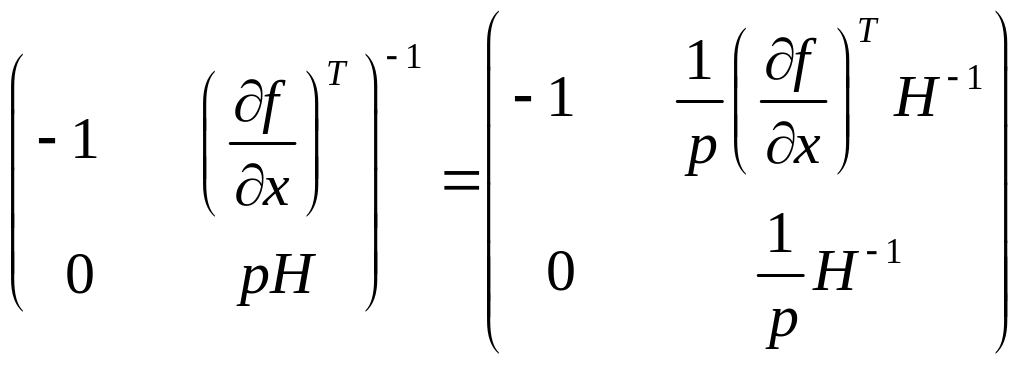тобто матричне рівняння (3.14) розв’язне відносно невідомих

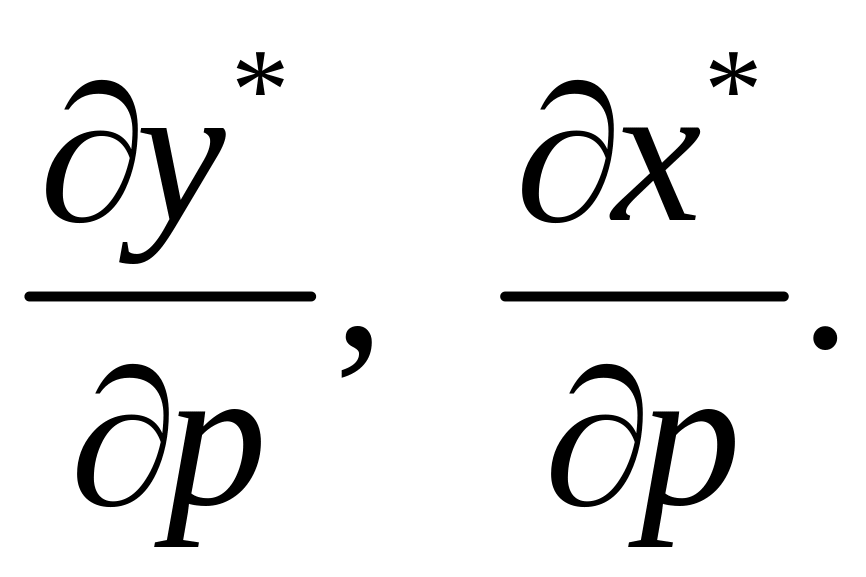
Рівняння реакції виробника на зміну цін ресурсів.

Нехай змінилась ціна -го ресурсу, тобто ціна . Продиференціюємо (3.11) по :

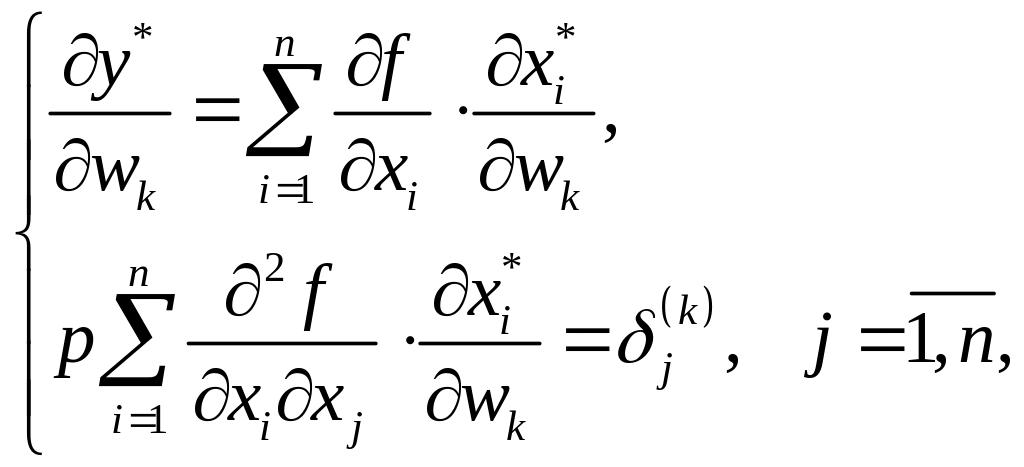(3.15)

де

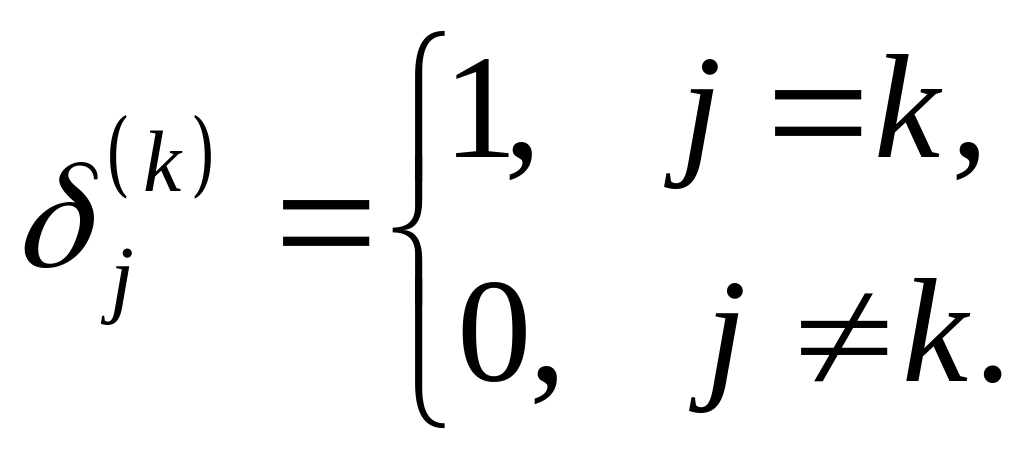
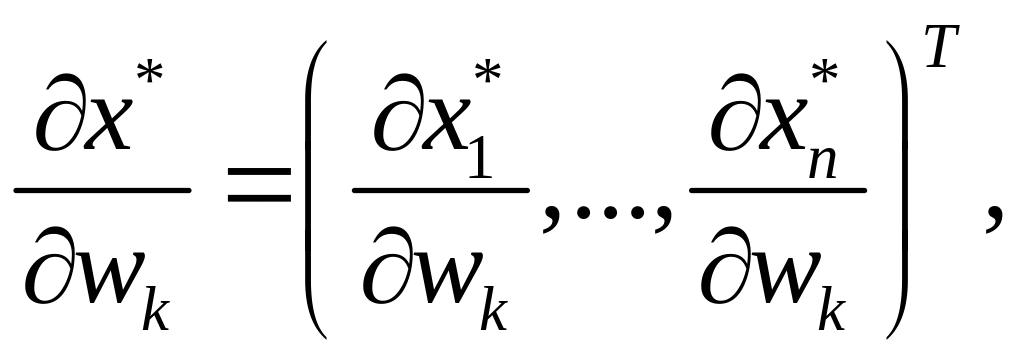
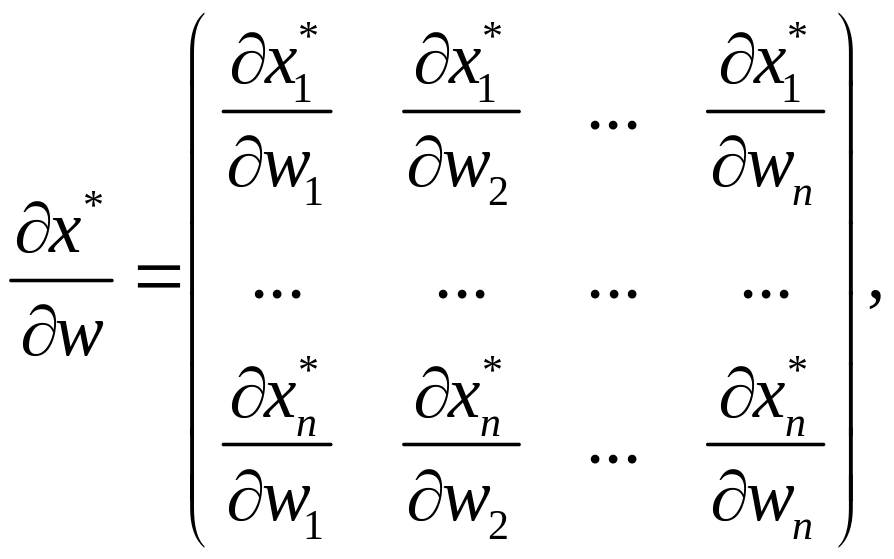
Позначивши 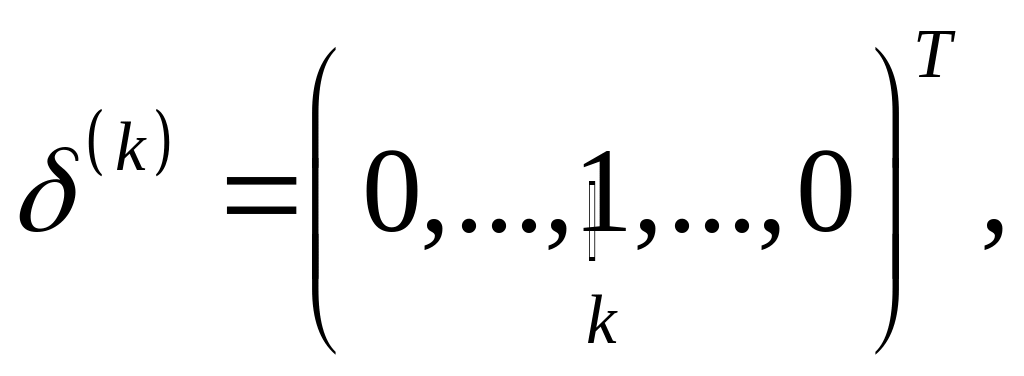систему (3.15) конкретизуємо так:

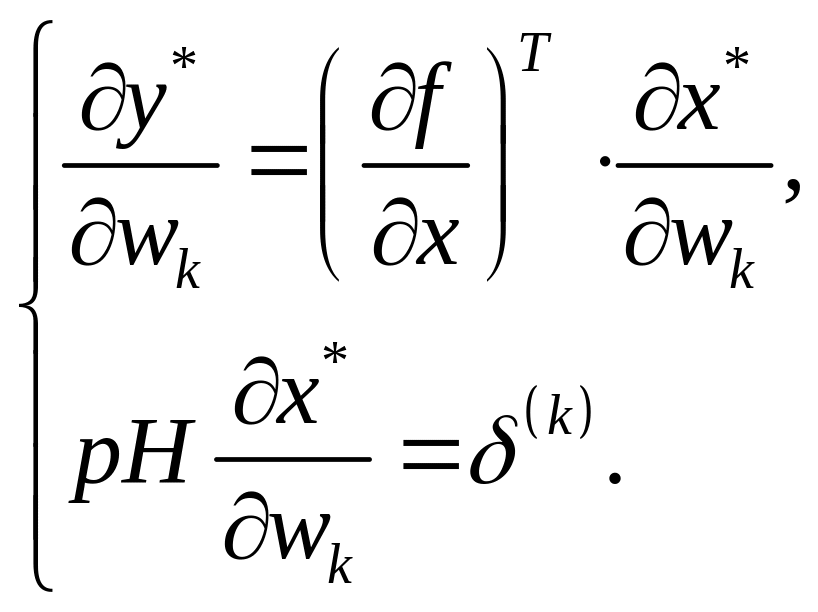(3.16)

Об’єднавши співвідношення (3.16) при всіх отримаємо

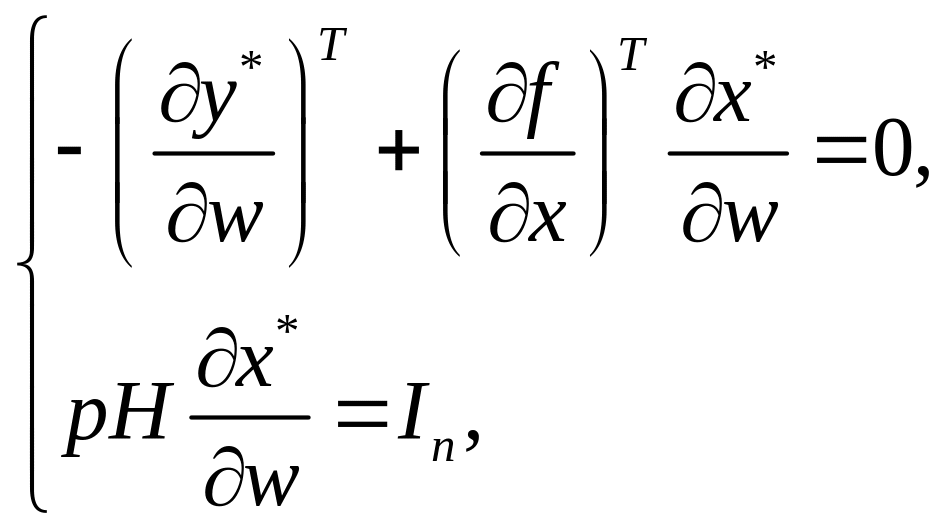(3.17)

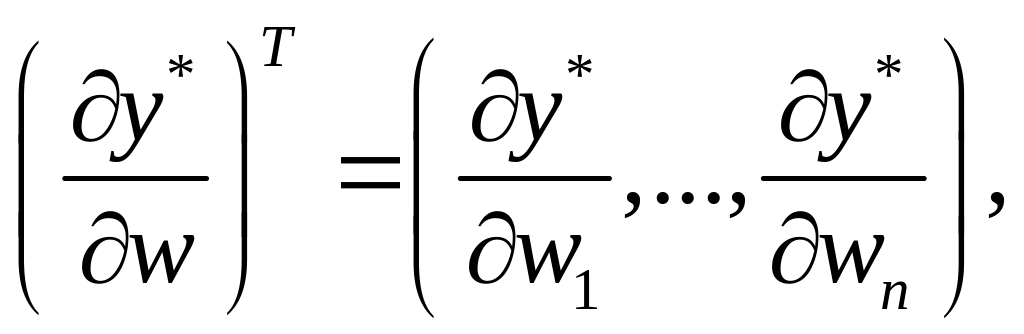
де – діагональна одинична матриця розмірності , – вектор-рядок. З іншого боку, систему (3.17) можна переписати у вигляді матричного рівняння

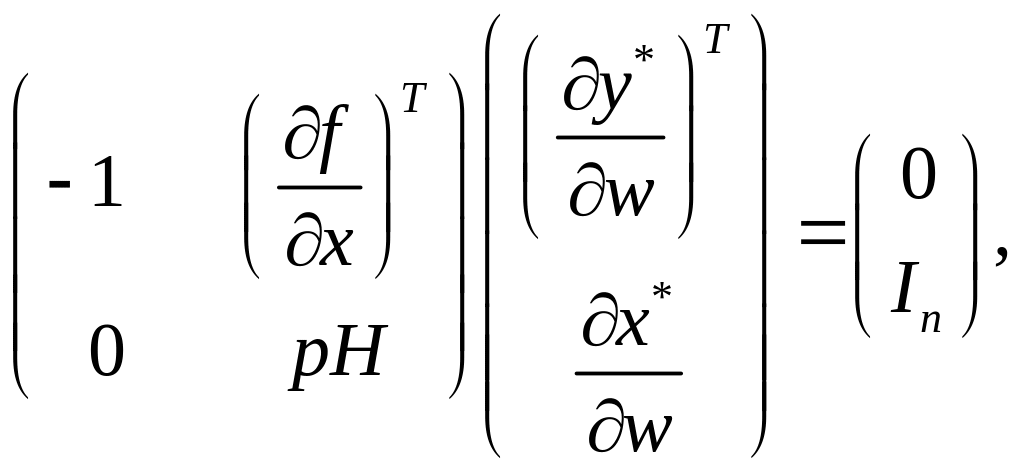(3.18)

де зліва – вектор-стовпець, а справа – – вектор-рядок. Рівняння (3.18) відображає реакцію виробника на зміну цін ресурсів.

Реакція виробника на одночасну зміну ціни випуску та цін ресурсів. Основне матричне рівняння теорії фірми.

Об’єднаємо матричні рівняння (3.14) і (3.18), після чого отримаємо основне матричне рівняння теорії фірми

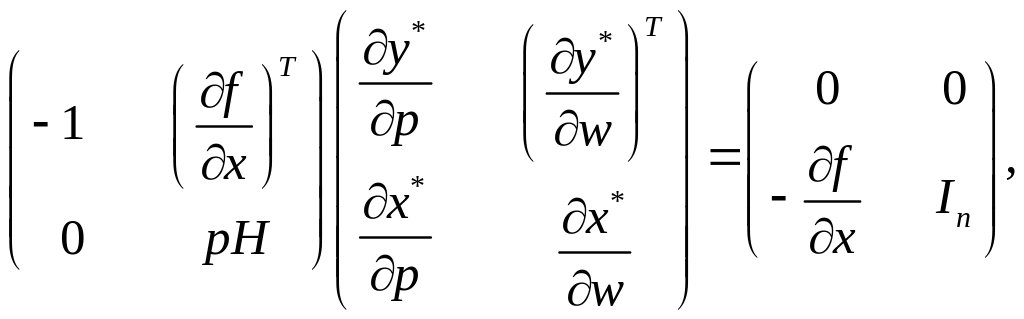(3.19)

де нулі (зліва на право) позначають відповідно вектор-стовпець, скаляр та вектор-рядок, що вже було уточнено раніше. Рівняння (3.19) показує реакцію виробника на одночасну зміну ціни випуску і цін ресурсів. Враховуючи, що існує обернена матриця до матриці

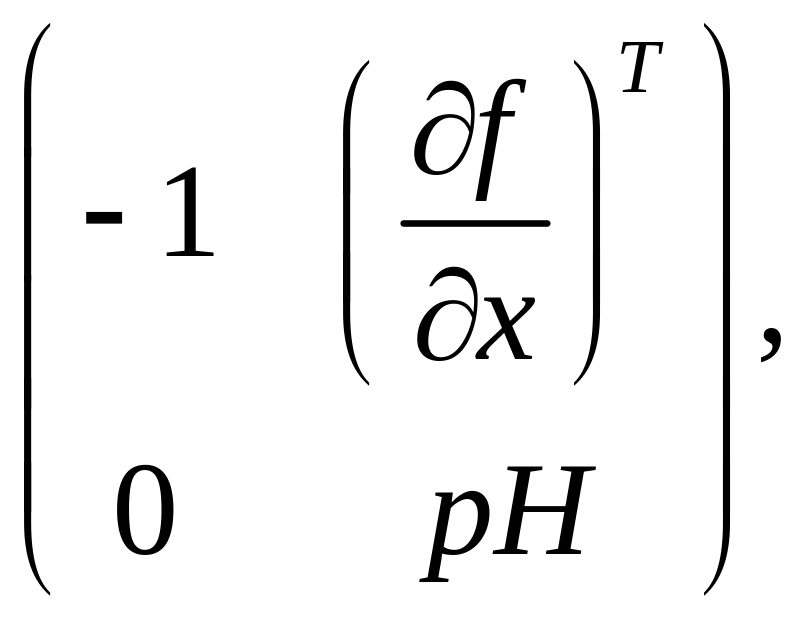
рівняння (3.19) можна розв’язати відносно змін випуску 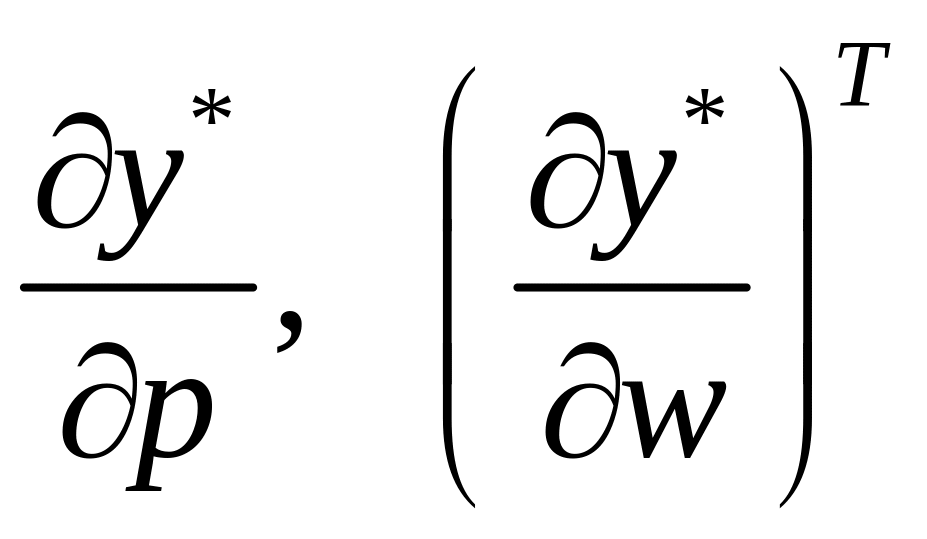та попиту на ресурси :

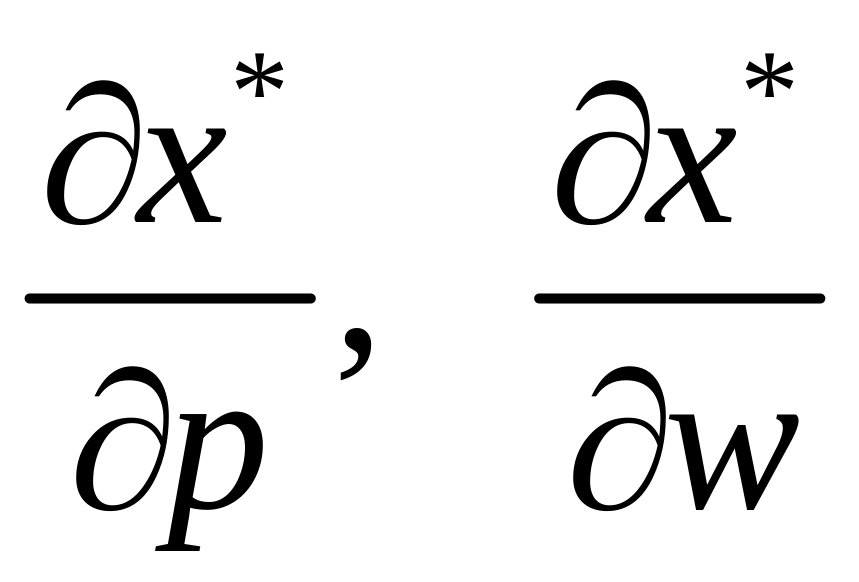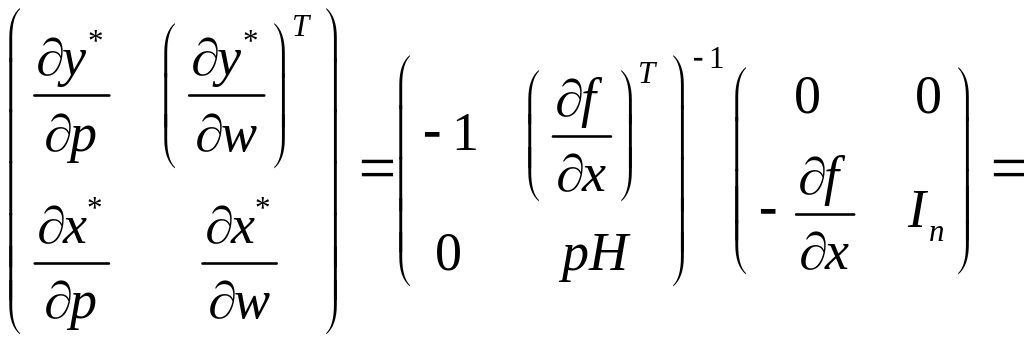
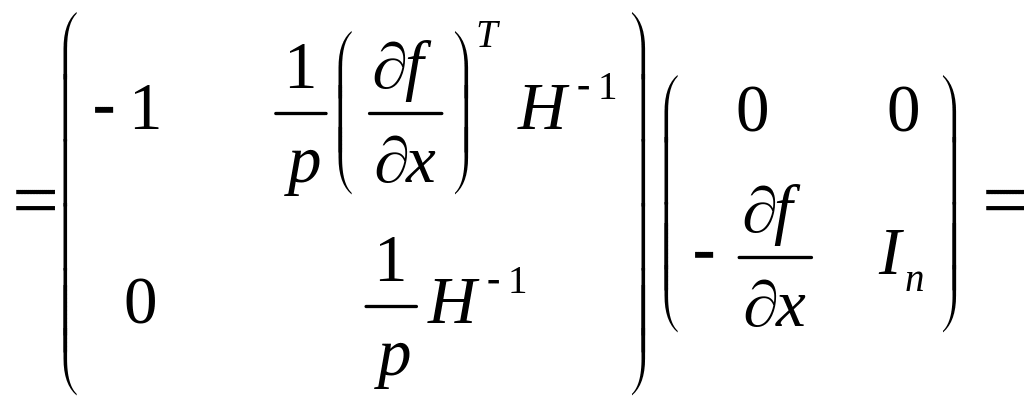
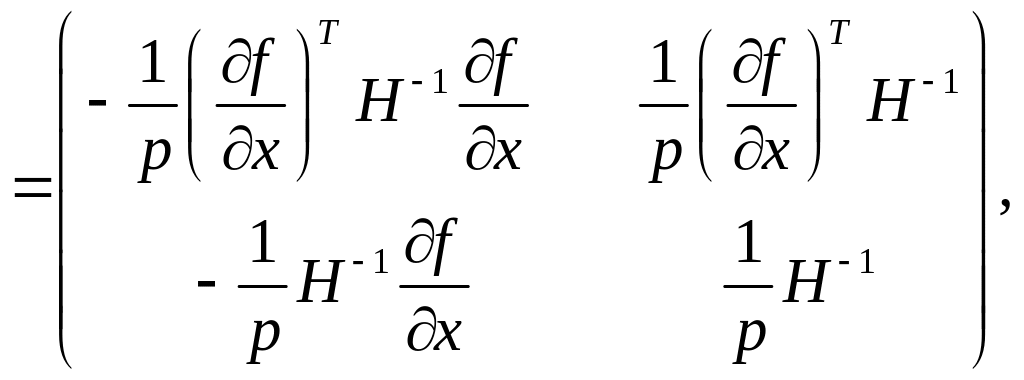
тобто

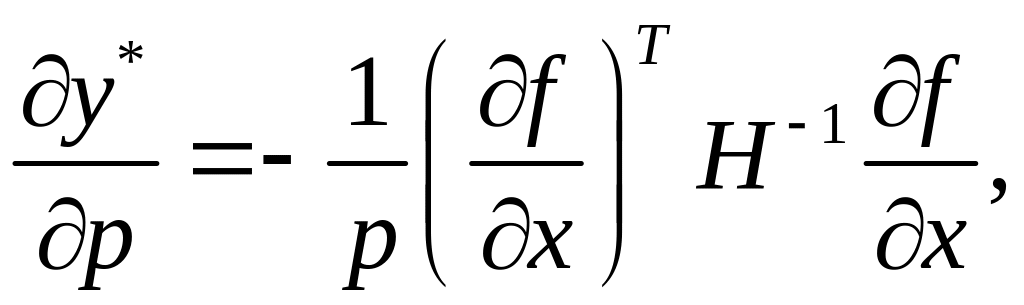(3.20)

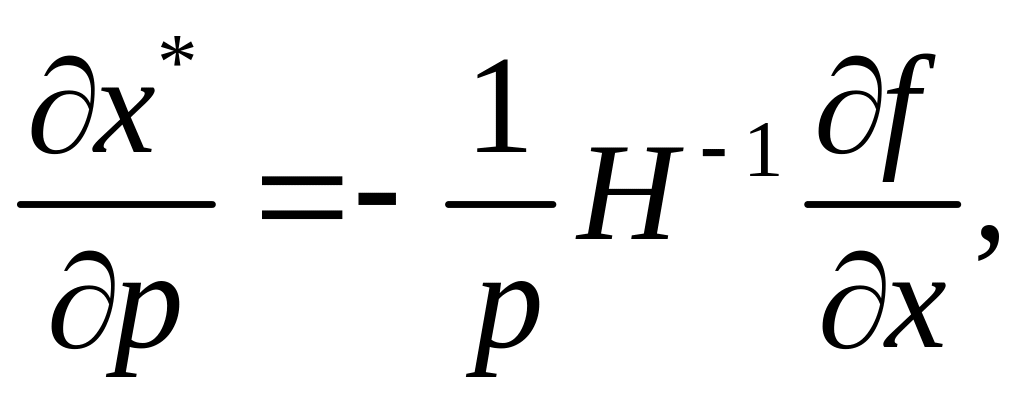(3.21)

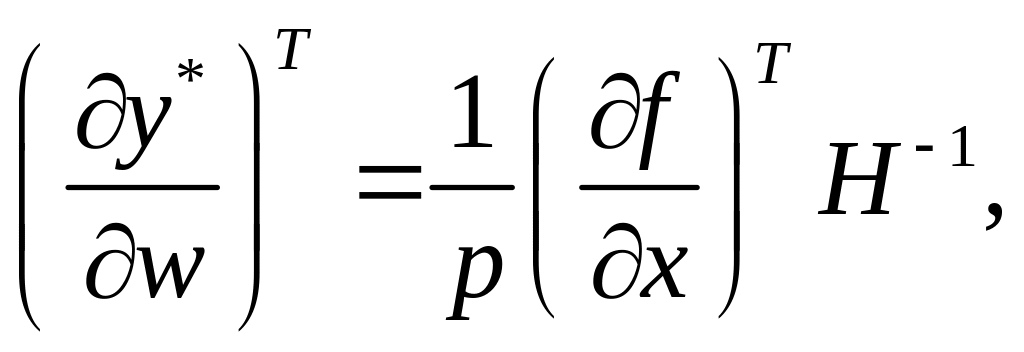(3.22)

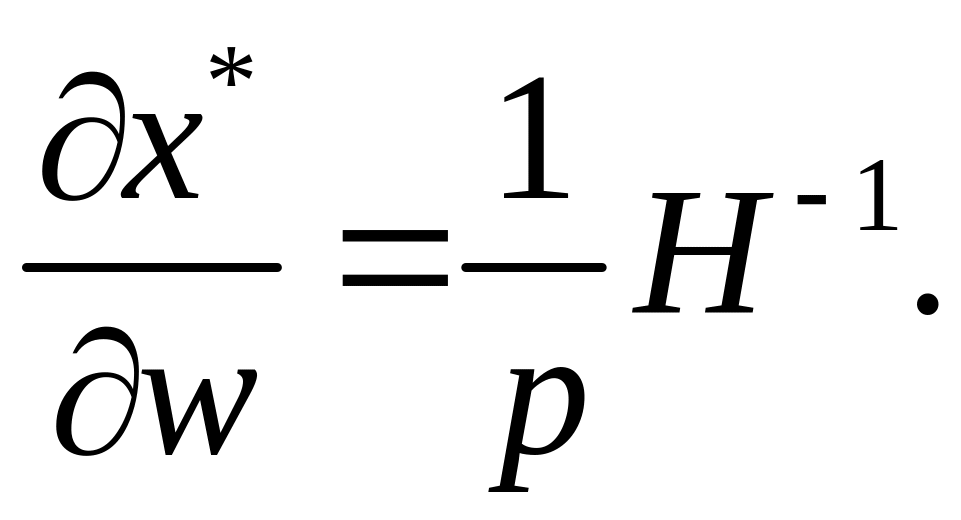(3.23)