3. Функції попиту та граничної вартості грошей.

Повернемось до моделі (1.7), яка є задачею опуклого програмування. Параметри та не обов’язково можуть бути фіксованими. Нехай , а Тоді споживач має справу із сім’єю задач

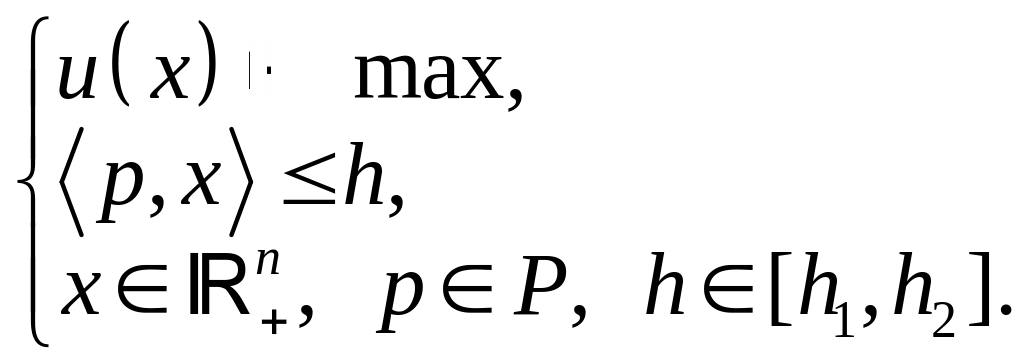(1.24)

При раніше прийнятих припущеннях при кожному фіксованому та (1.24) буде мати єдиний розв’язок із відповідним єдиним оптимальним множником Лагранжа .

Означення 1.9. Визначені на множині числові функції та називаються відповідно функціями попиту та граничної вартості грошей.

Зрозуміло, що – це вектор-функція, а – скалярна функція. Як випливає з (1.24) функція попиту є однорідною функцією нульового степеня (попит інваріантний відносно пропорційних змін цін і доходу), тобто при всіх

. (1.25)

Крім того, як випливає з (1.25) для будь-якої -тої компоненти функції та будь-якої ціни справджується співвідношення:

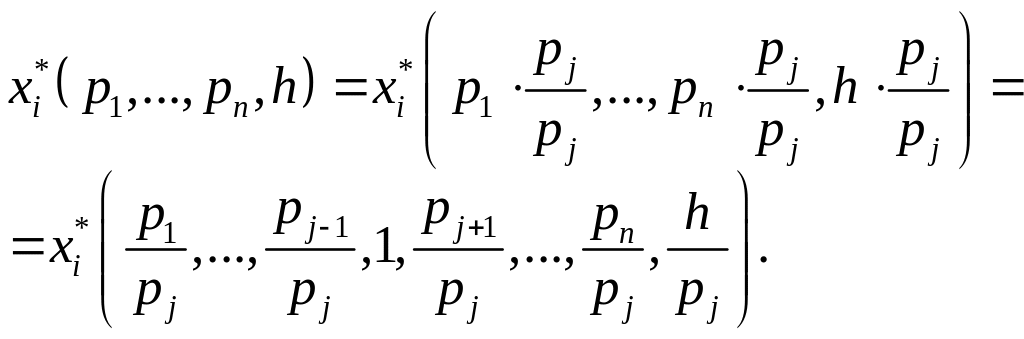(1.26)

Інтерпретація рівності (1.26) така: попит на будь-який товар залежить лише від відношення цін які називаються відносними цінами, та від відношення грошового доходу , який називається реальним доходом споживача.

При цьому ціну на -й товар можна назвати визначальною, базовою. Вона береться за одиницю розрахунків.

Що стосується процесу побудови функцій попиту та граничної вартості грошей, то зрозуміло, що він безпосередньо пов’язаний з процесом розв’язання задач (1.24). Проілюструємо це на конкретному прикладі.

4. Рівняння Слуцького у векторній та матричній формі. Матриця Слуцького і її властивості.

Рівняння зміни попиту в залежності від зміни ціни одного з товарів.

З’ясуємо спочатку, як зміниться попит споживача, якщо зміниться (наприклад, зросте) ціна товару . При цьому всі інші ціни та величину доходу споживача будемо вважати постійними . Якщо ціна -го товару зросла на , то з урахуванням того, що при фіксованих 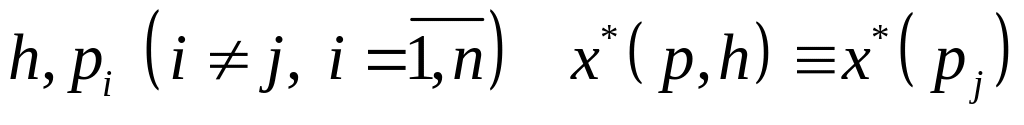і 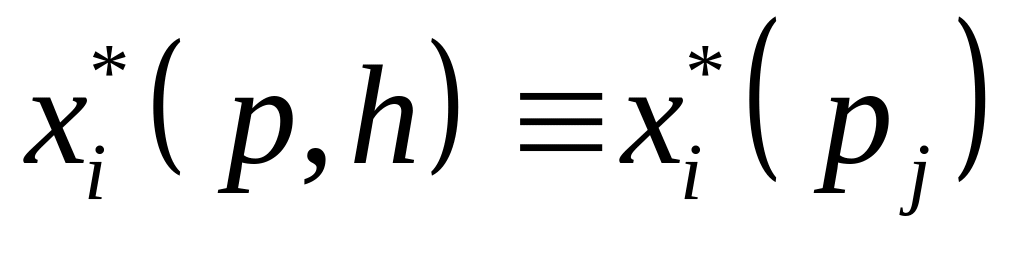маємо:

.

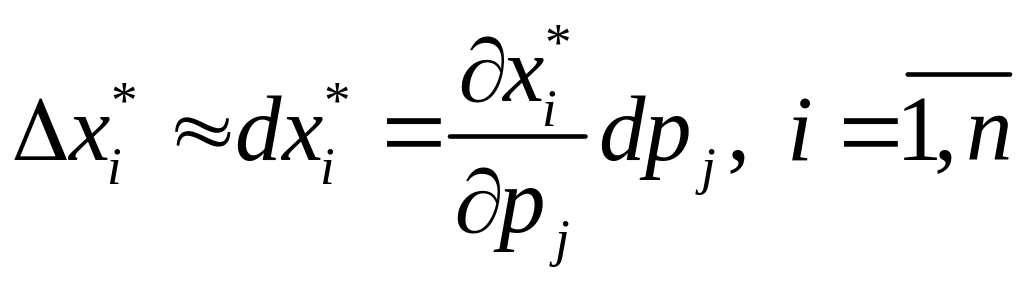Рівняння для визначення похідних 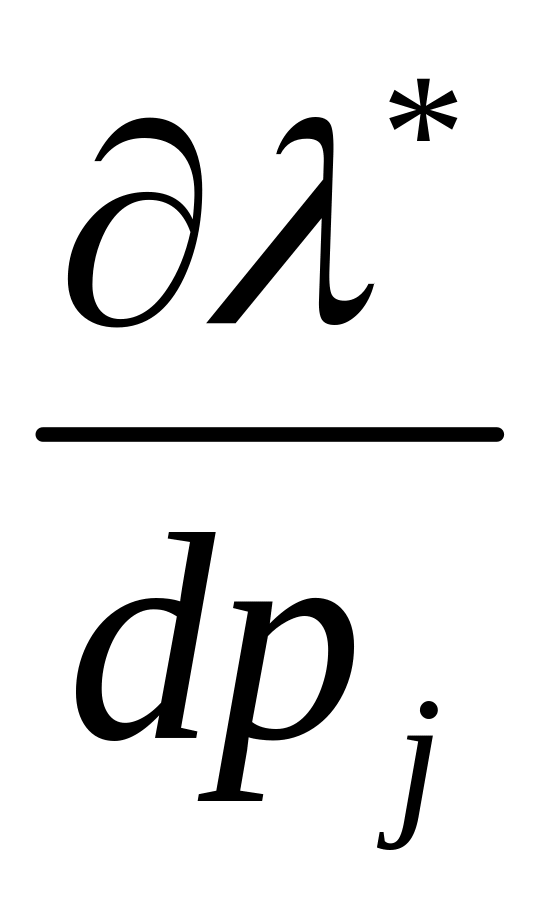та 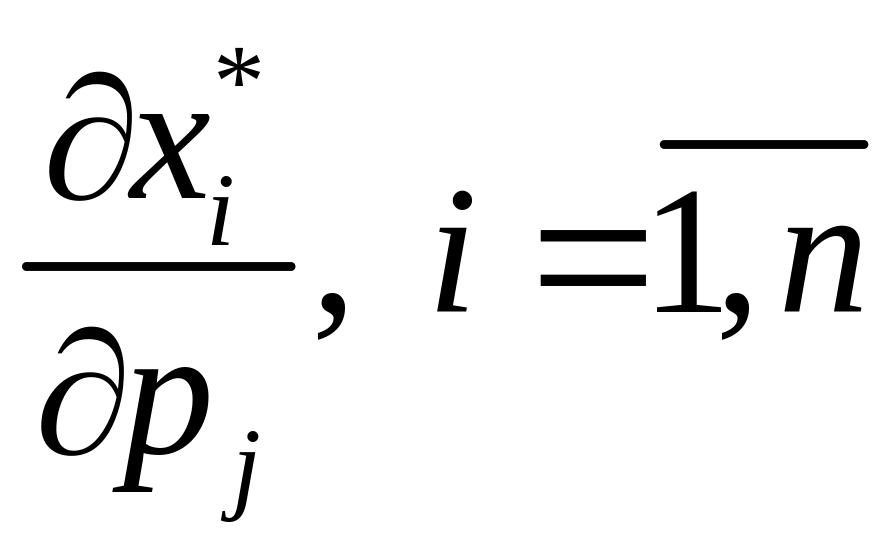, одержимо, продиференціювавши (1.17) по :

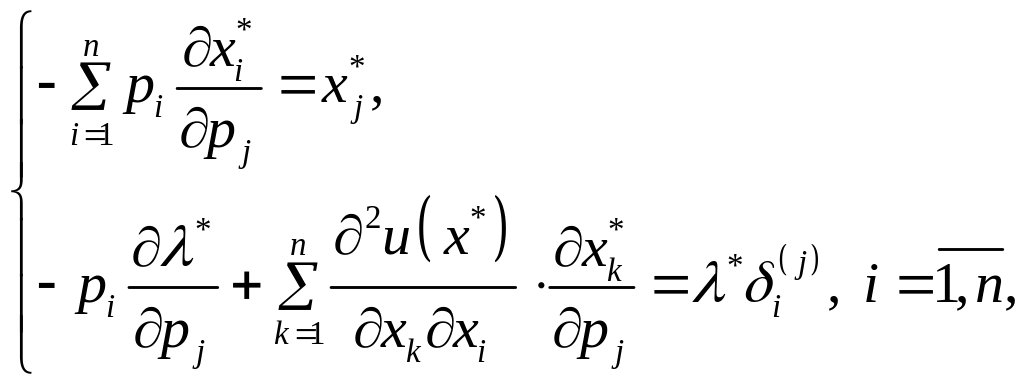(1.32)

де символ Кронекер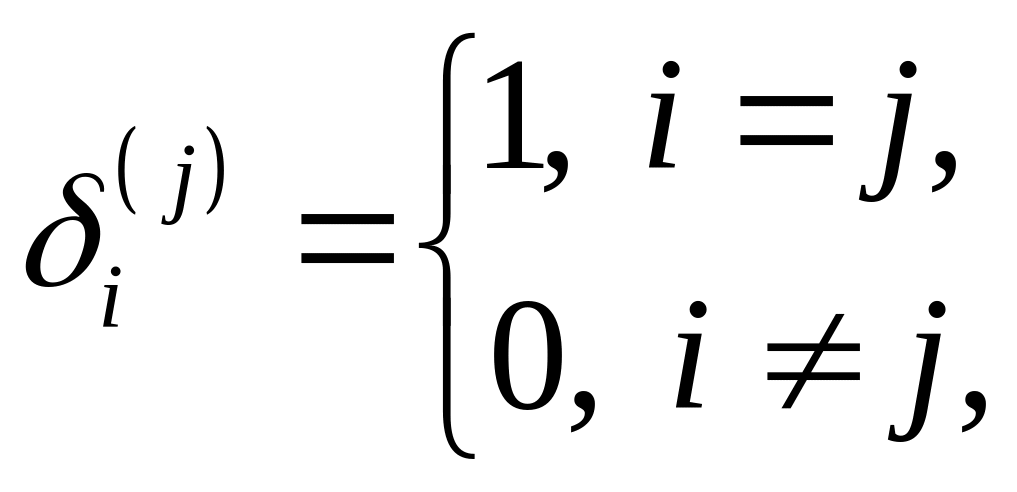а а

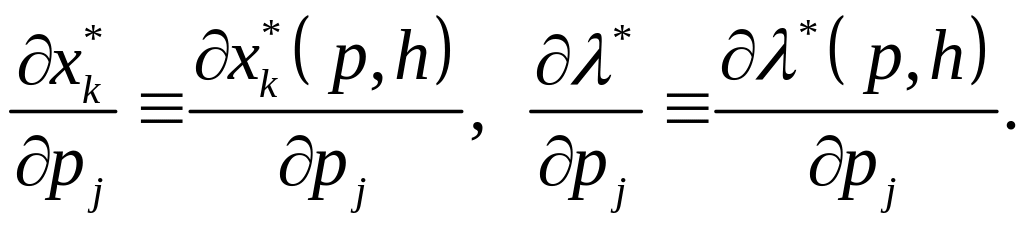
Система (1.32) є визначеною, оскільки складається з рівнянь відносно невідомих

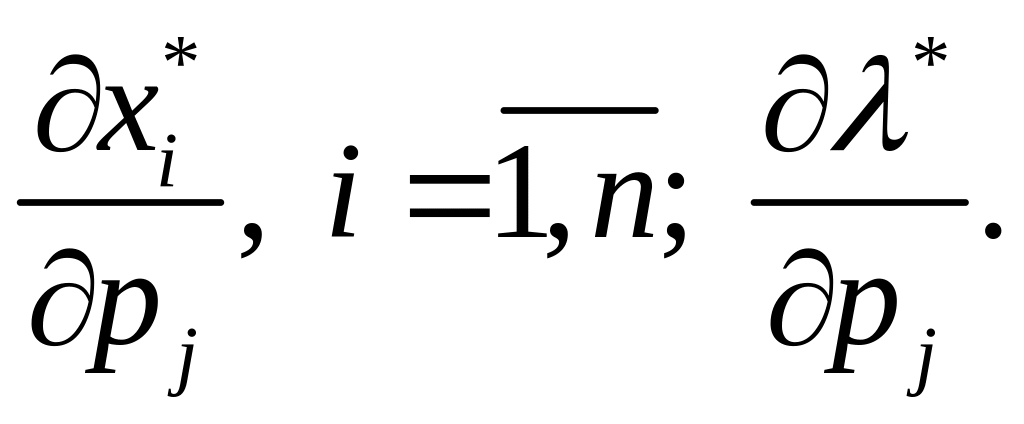
У векторно-матричній формі система (1.32) запишеться так:

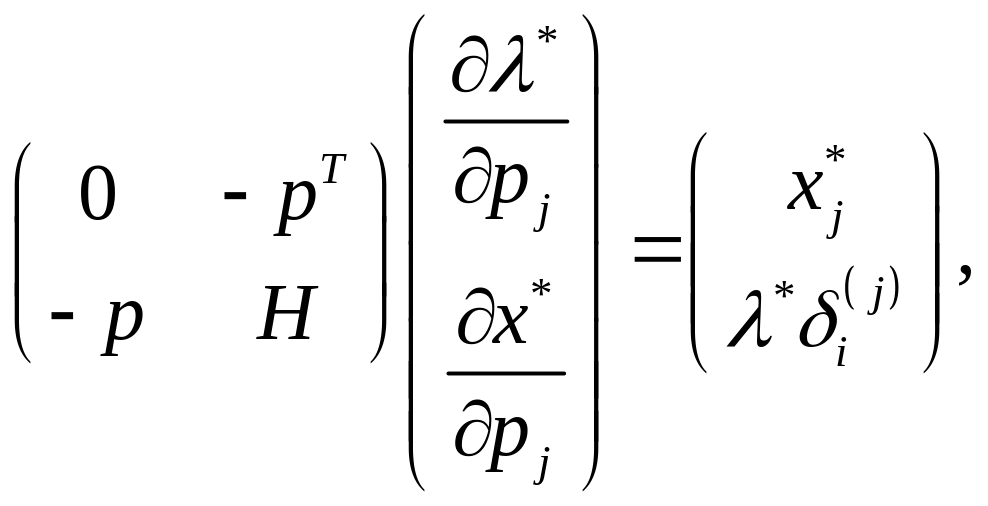(1.33)

де 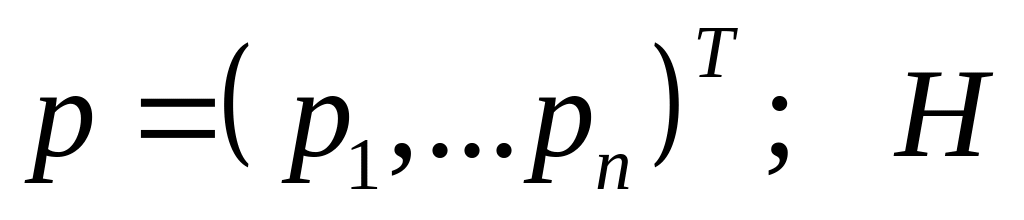– матриця Гессе для функції корисності; 0 і 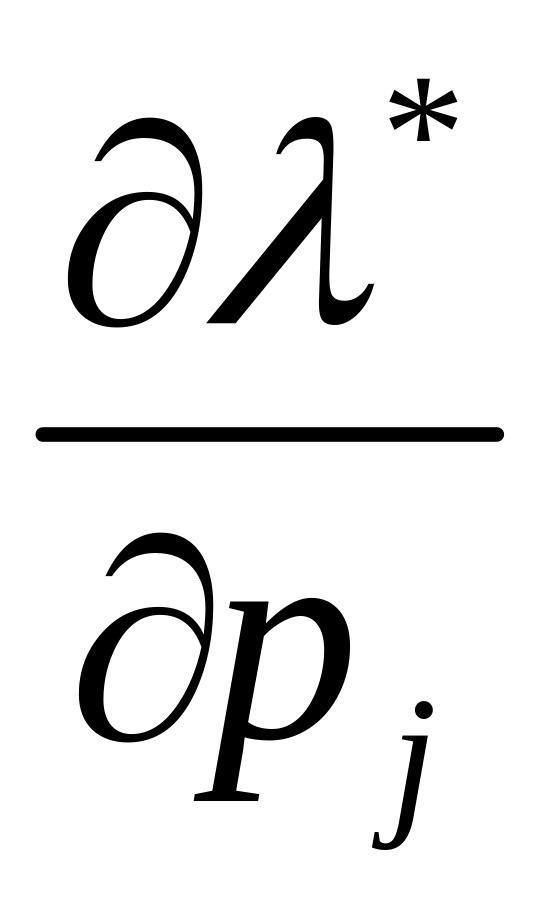– скалярні величини;

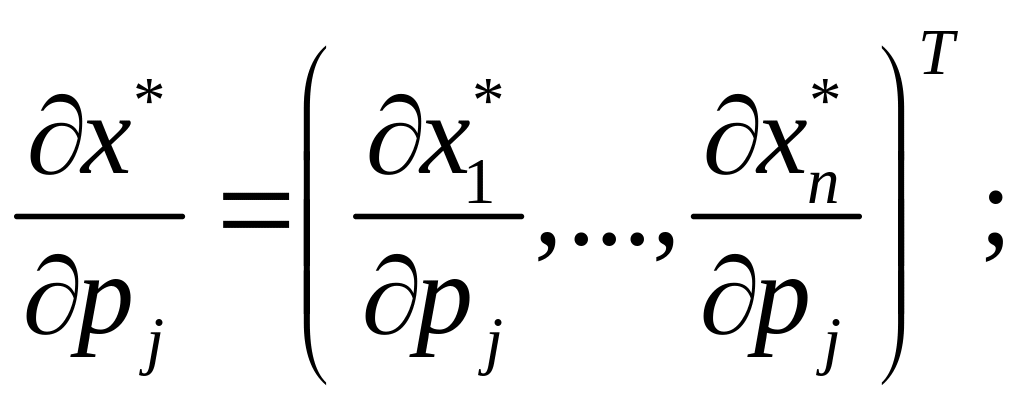
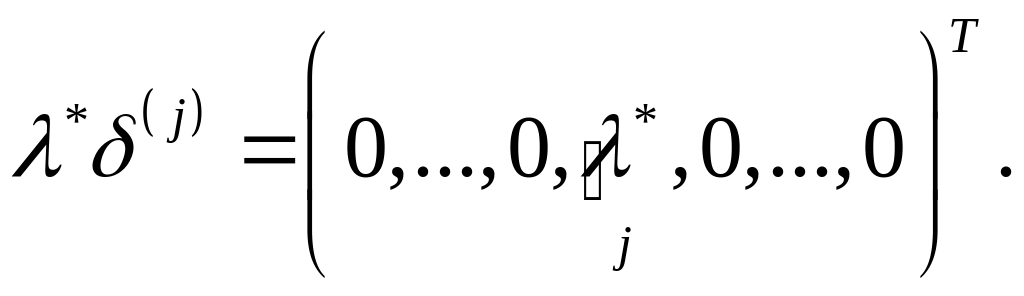
Як відомо, матриця Гессе є невиродженою (вона є від’ємно визначеною). З урахуванням цього на основі безпосередньої перевірки можна встановити співвідношення

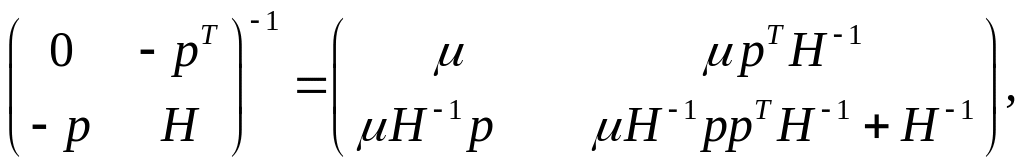(1.34)

де число

Врахувавши (1.34), розв’язок системи (1.33) можна представити у вигляді:

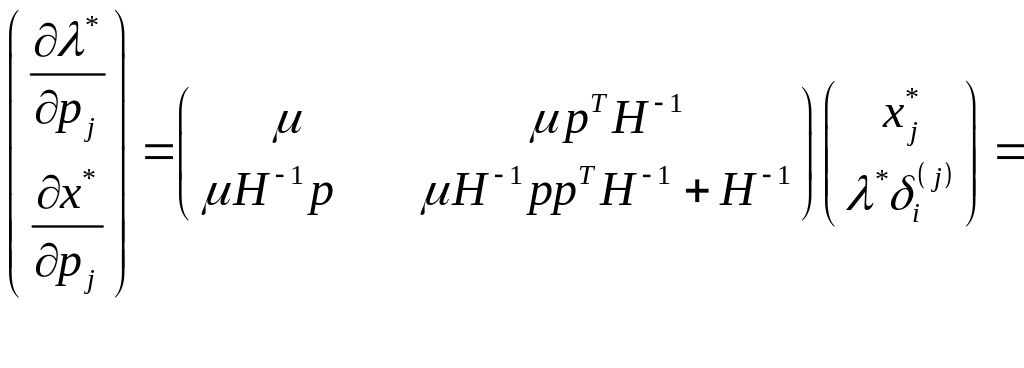
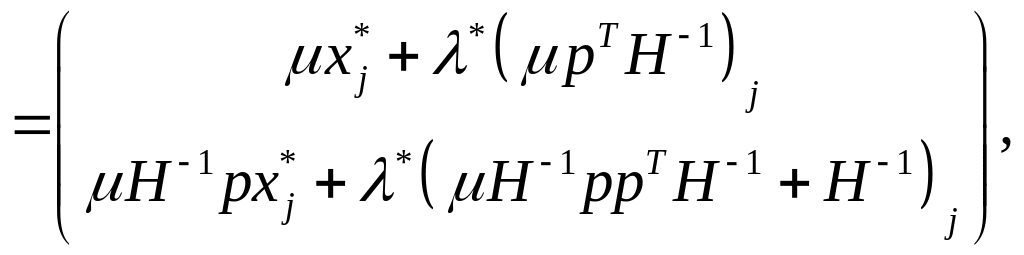(1.35)

де індекс біля матриці, взятої у дужки, означає, що взятий її -й стовпець. Векторна рівність (1.35) підтверджує, що збільшення ціни на -й товар приводить до змін попиту на всі товари, причому величини цих змін конкретизуються вектором

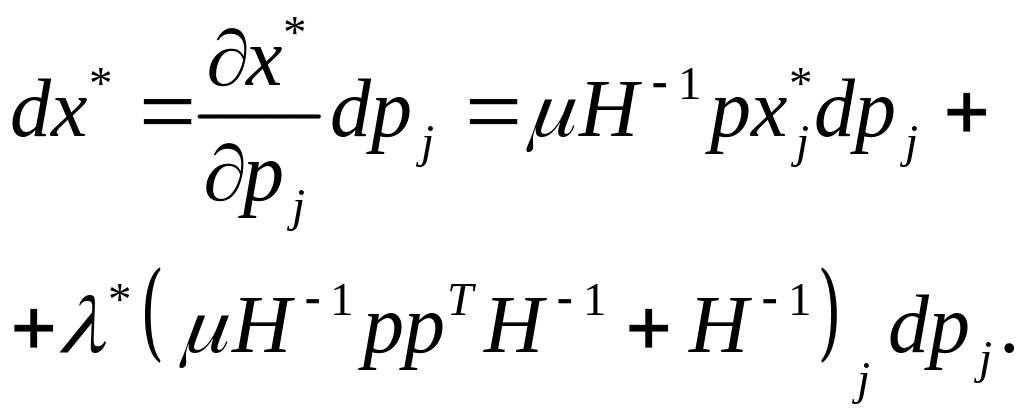
Рівняння зміни попиту в залежності від зміни компенсованої ціни одного з товарів.

Тепер розглянемо таке збільшення доходу яке компенсує споживачу збільшення ціни Згідно з теорією споживання це означає, що корисність споживача має зберегтись на попередньому рівні, тобто З перших рівнянь (1.17) випливає, що

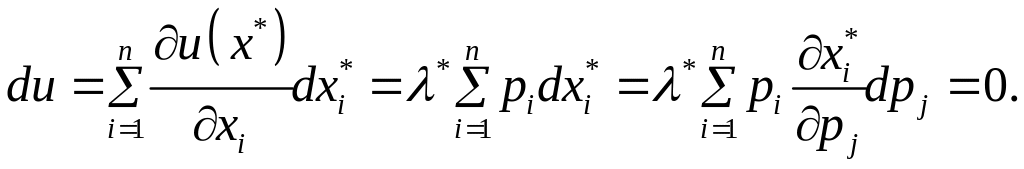
Отже, корисність буде сталою, якщо

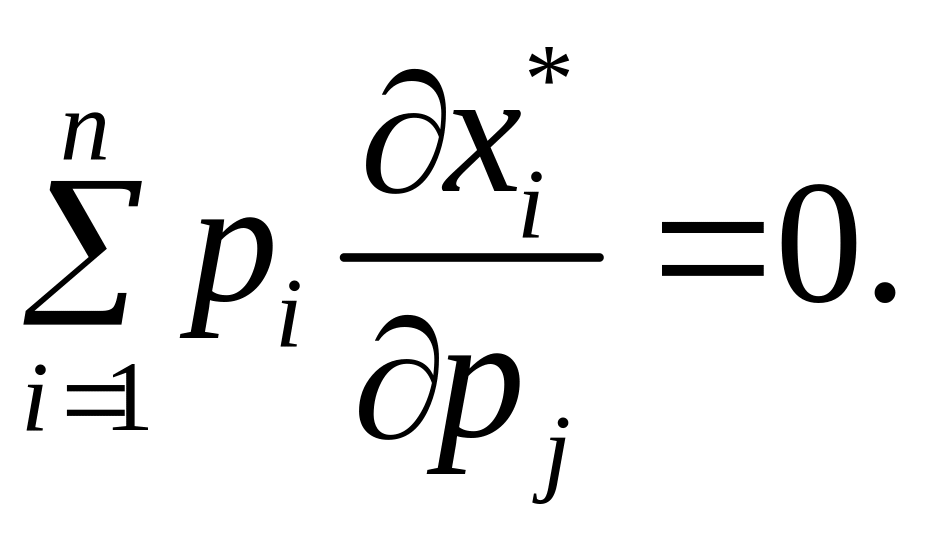(1.37)

Використавши -е рівняння (1.17) та (1.37), одержимо співвідношення:

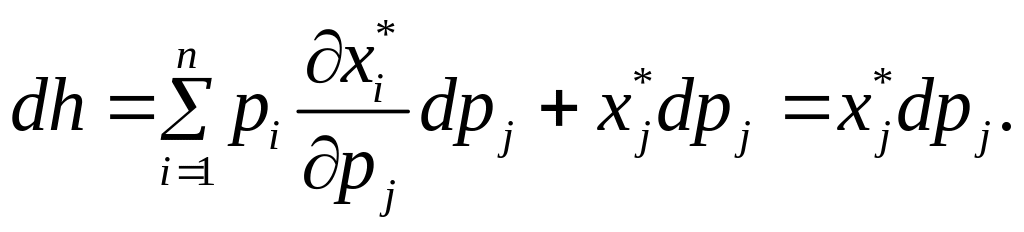(1.38)

З (1.38) можна дійти висновку: дохід споживача збільшиться рівно настільки, скільки потрібно споживачу на додаткові витрати при покупці -го товару в попередньому обсязі, якщо ціна зросте на 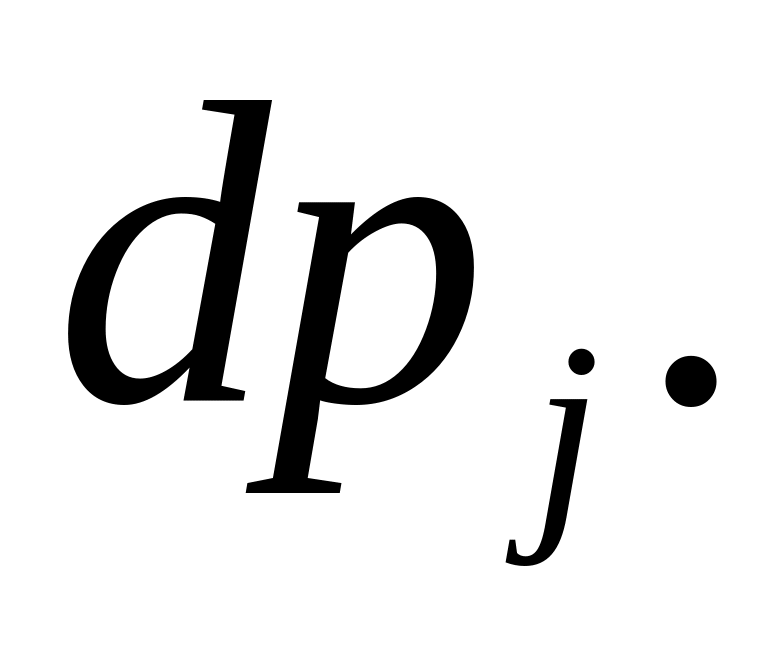Замінивши першу рівність у (1.32) на рівність (1.37), отримаємо для визначення 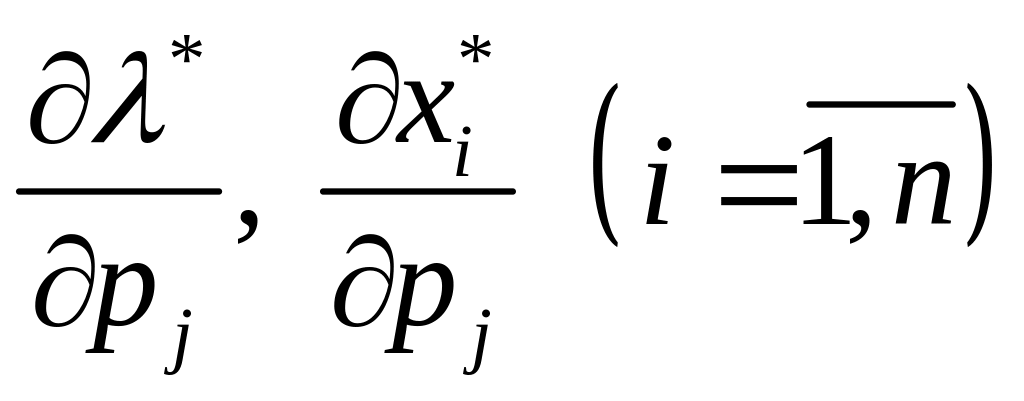при компенсованій зміні ціни таку систему рівнянь:

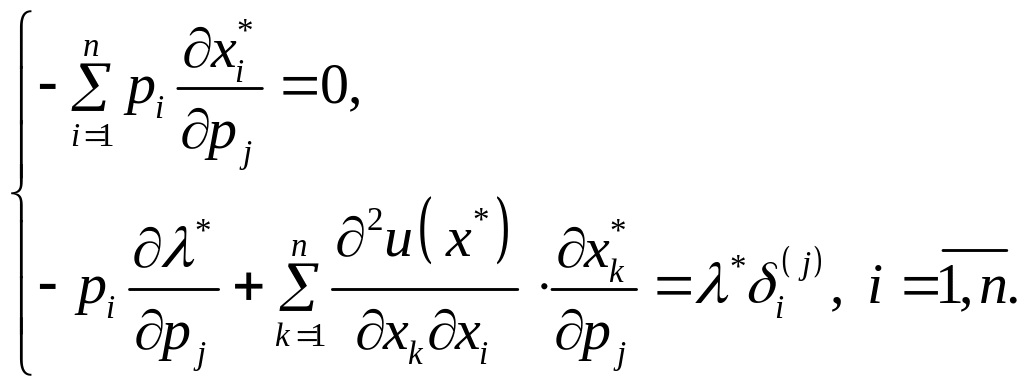(1.39)

Перепишемо (1.39) у векторно-матричній формі

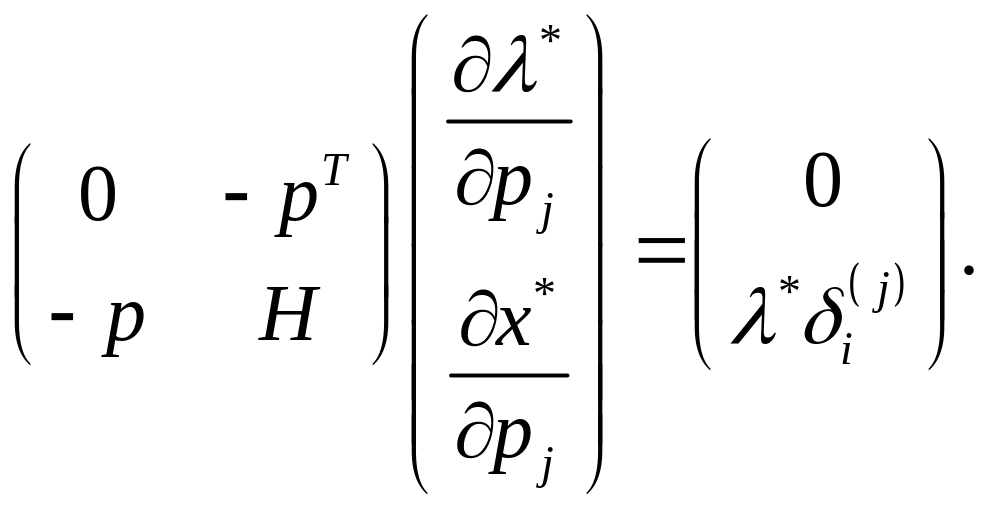(1.40)

З урахуванням (1.34) розв’язок системи (1.40) формалізується таким чином:

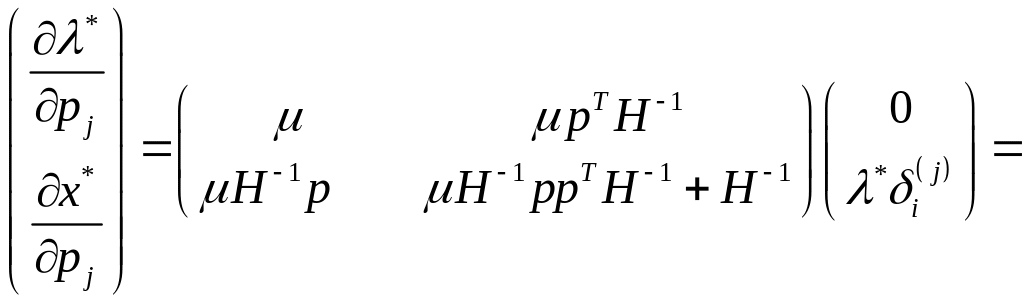
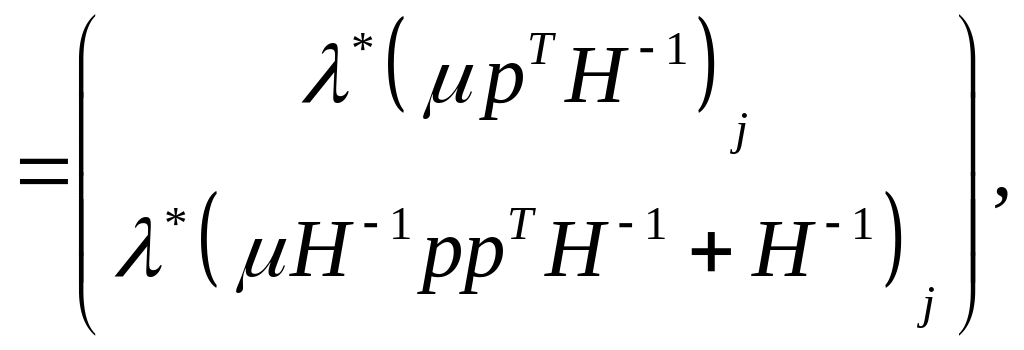(1.41)

де, як і раніше, індекс вказує на -й стовпець відповідної матриці. З (1.41) випливає, що збільшення ціни на -й товар з компенсацією приводить до зміни попиту, що вимірюється вектором

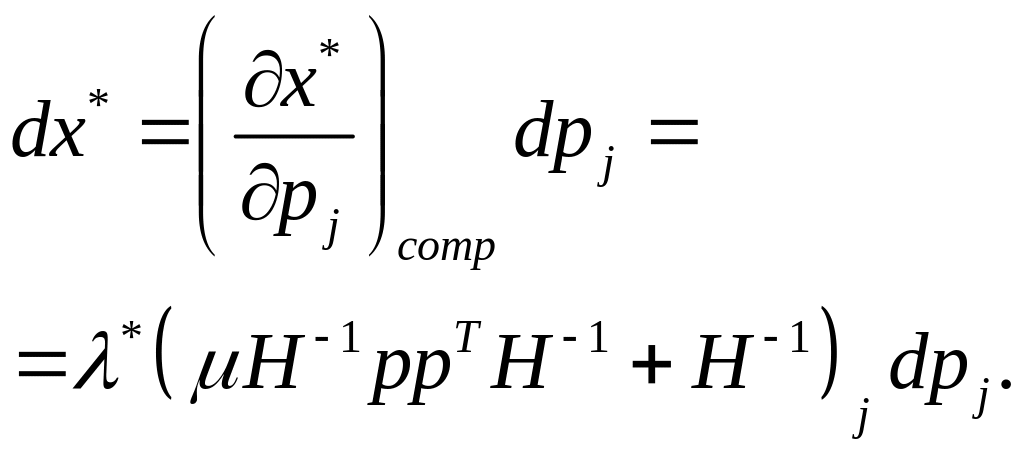(1.42)

Інакше кажучи, другий доданок в правій частині (1.36) збігається з (1.42) і показує зміну попиту у тому випадку, коли збільшення ціни -го товару на компенсується збільшенням доходу

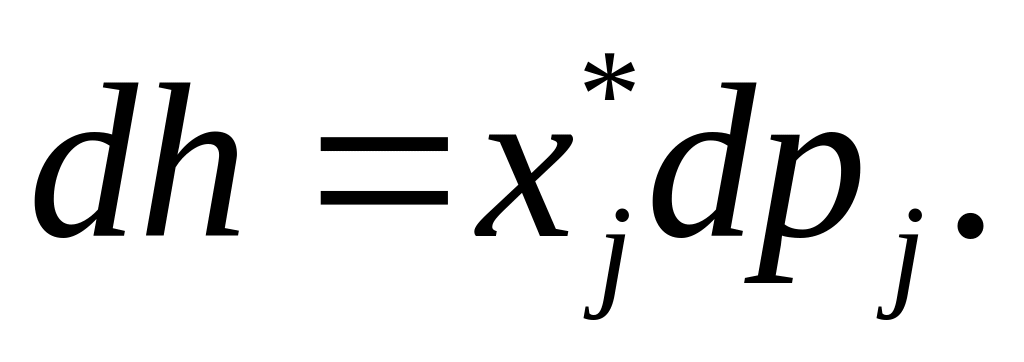
Рівняння зміни попиту в залежності від зміни доходу.

Нехай дохід змінився на величину Тоді попит (вектор вважаємо фіксованим) зміниться на величину 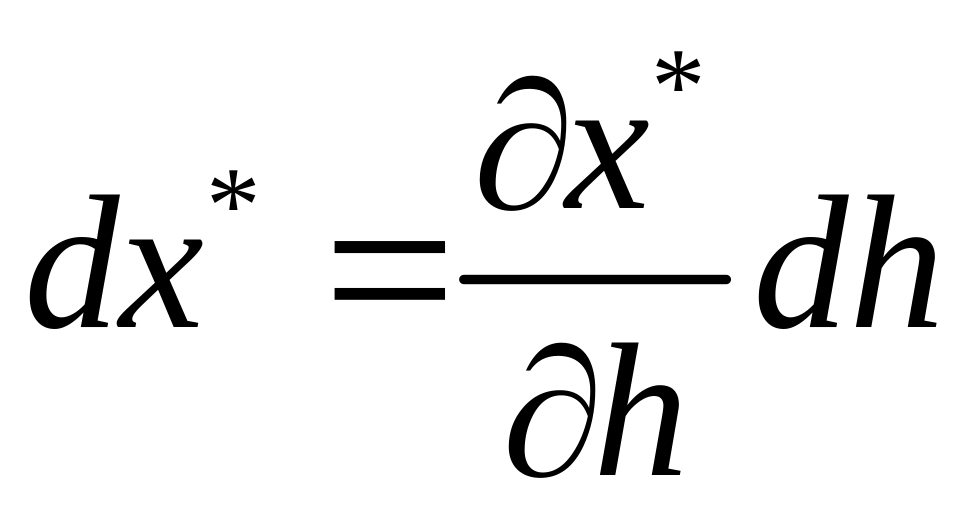. Рівняння для 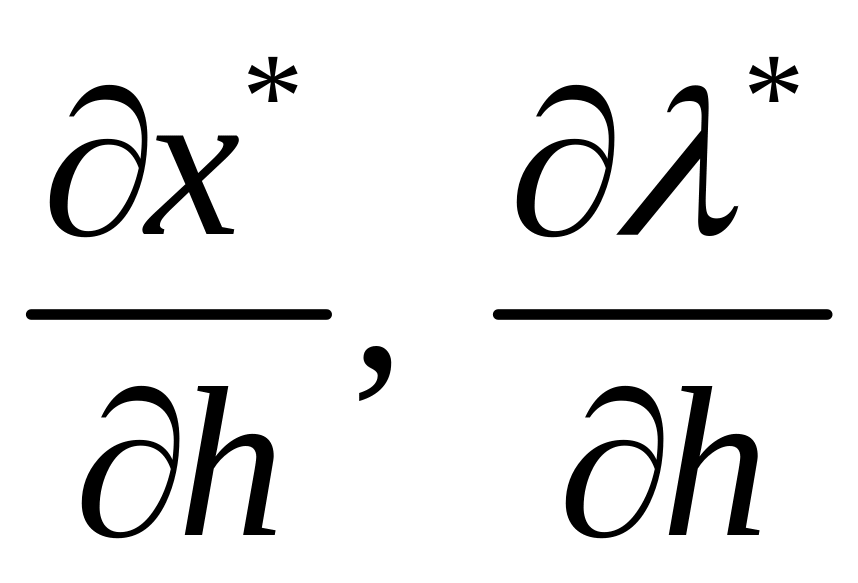знову отримаємо, продиференціювавши (1.17) по :

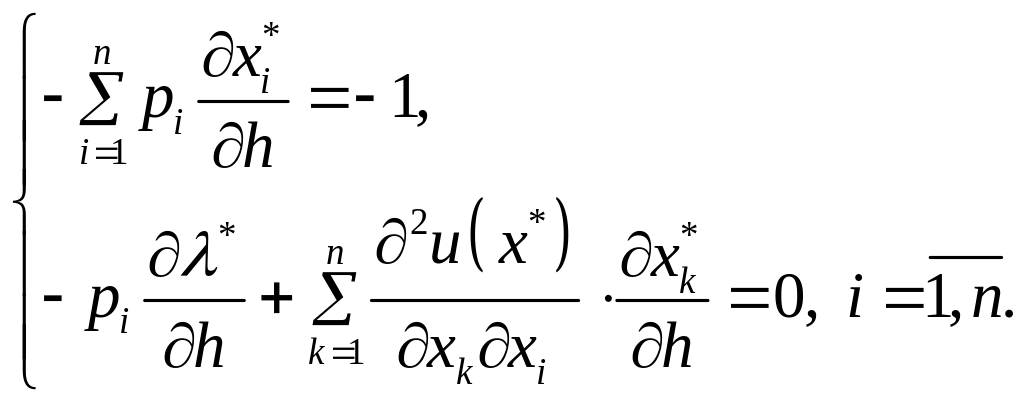(1.43)

Перепишемо систему (1.43) у векторно-матричному вигляді:

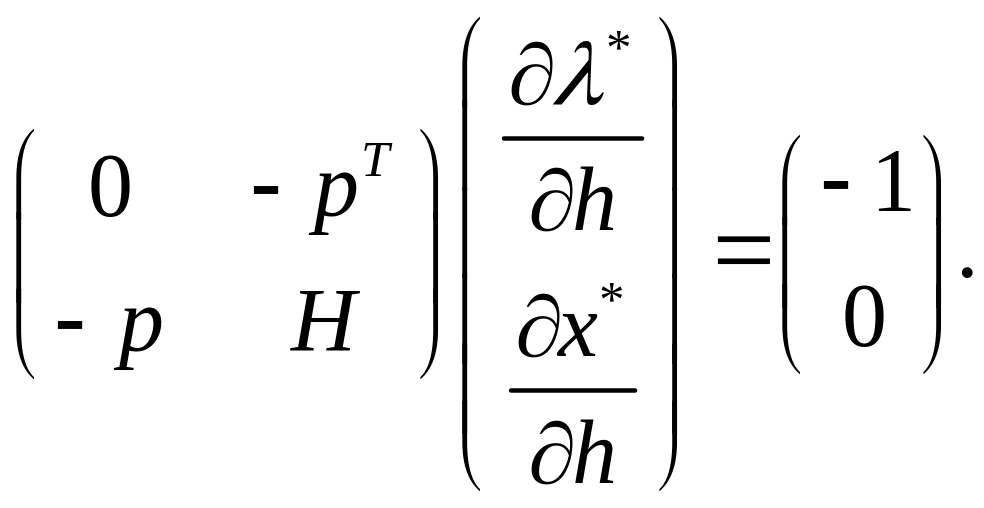(1.44)

Зазначимо, що у (1.44) 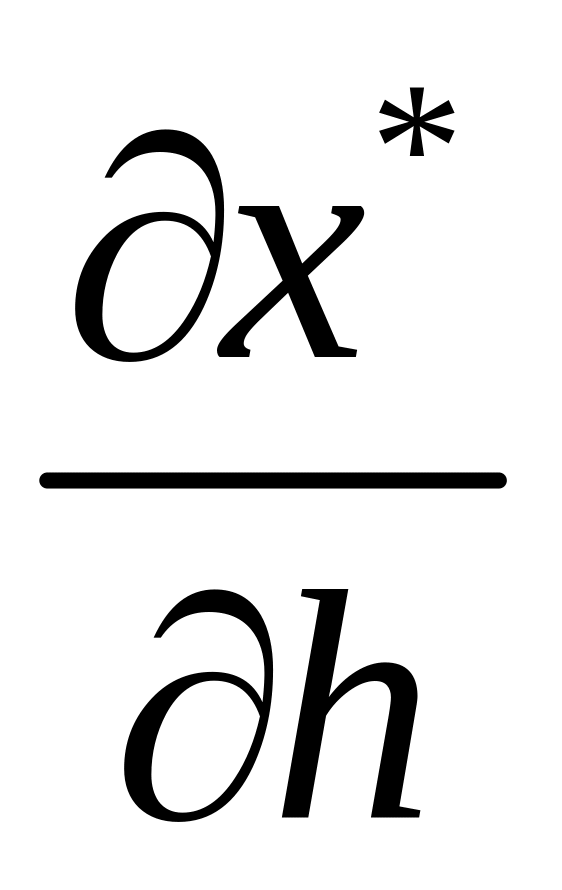і є -мірними векторами. Використавши (1.34) та (1.44), одержимо шуканий розв’язок:

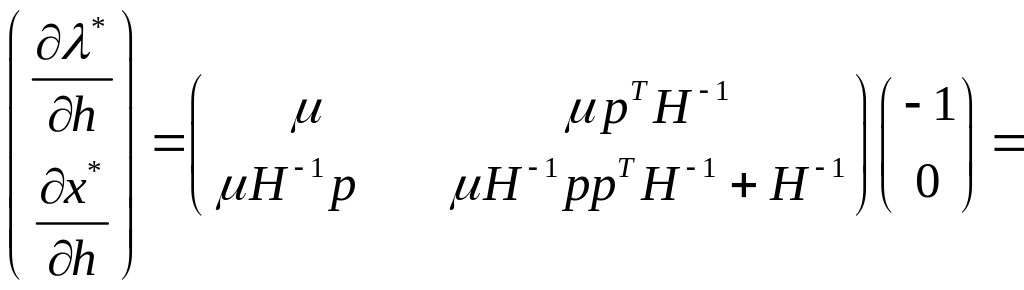
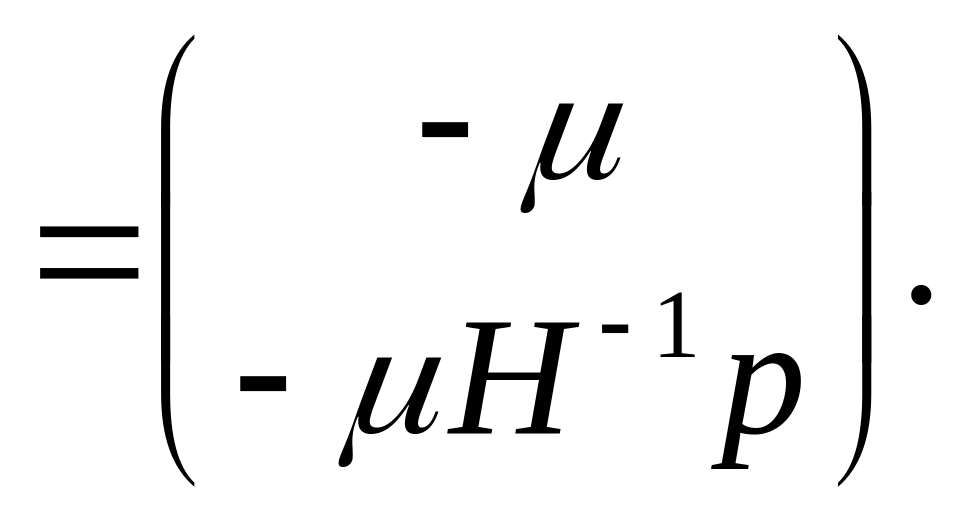(1.45)

Отже, рівність (1.45) показує, що 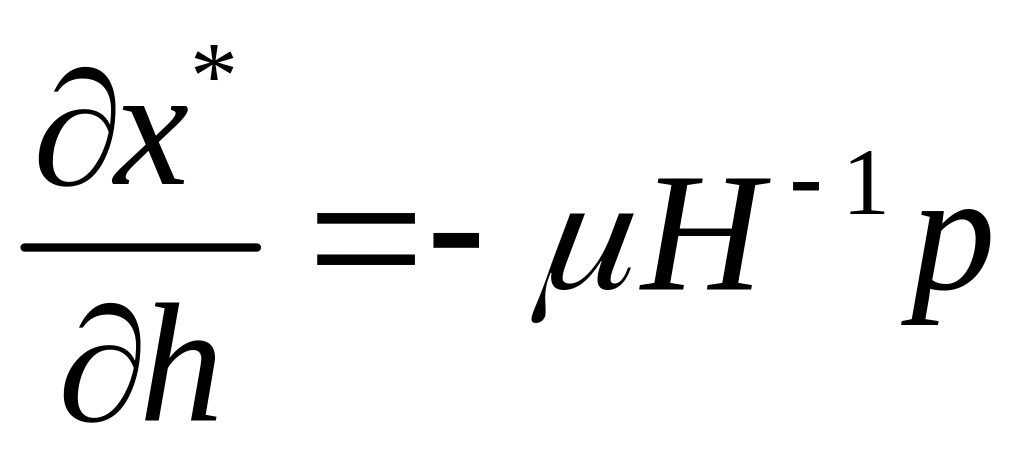і зміна доходу на величину приводить до зміни вектора попиту на вектор

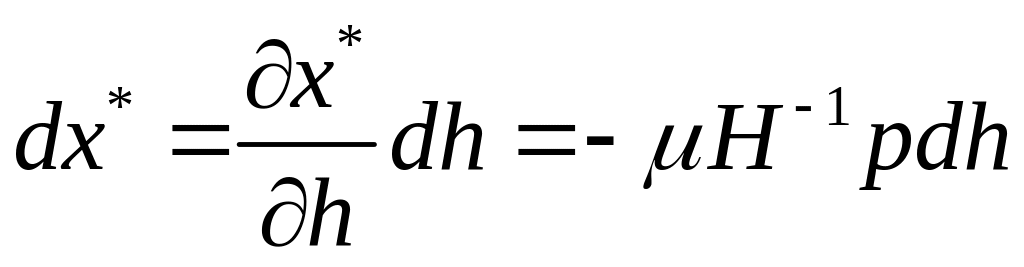. (1.46)

Рівняння Слуцького. Властивості матриці Слуцького.

Об’єднуючи (1.36), (1.42) і (1.46), одержимо рівняння Слуцького:

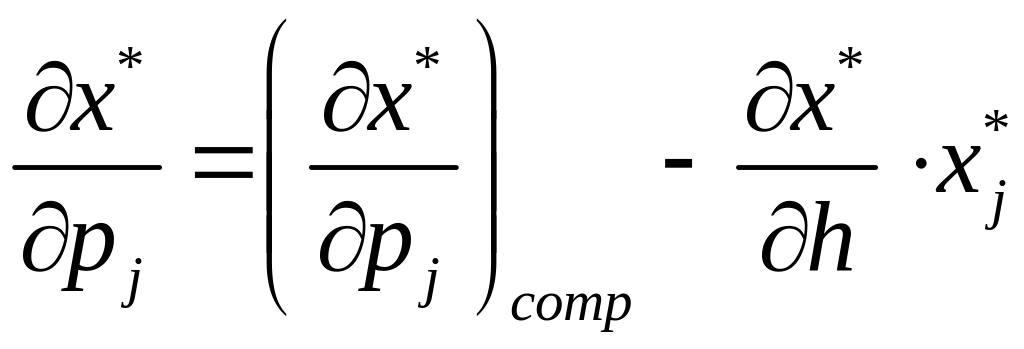. (1.47)

Рівняння Слуцького (1.47) описує загальний ефект від впливу на попит ціни, компенсованої ціни та доходу. Для застосування рівняння (1.47) потрібно знати властивості матриці Слуцького

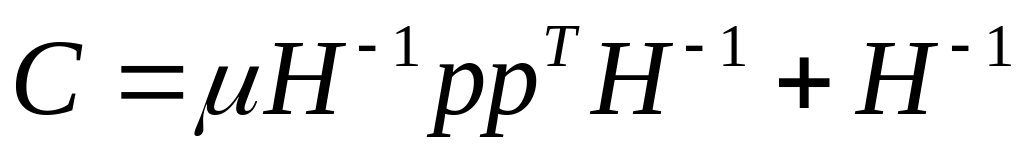,де .

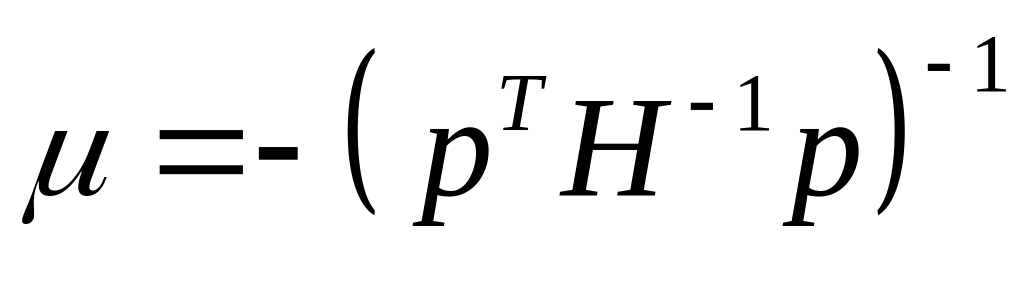1. – симетрична матриця, оскільки симетричними є матриці та .

2. – від’ємно напіввизначена матриця, тобто для будь-якого вектора виконується умова: .

3. Якщо 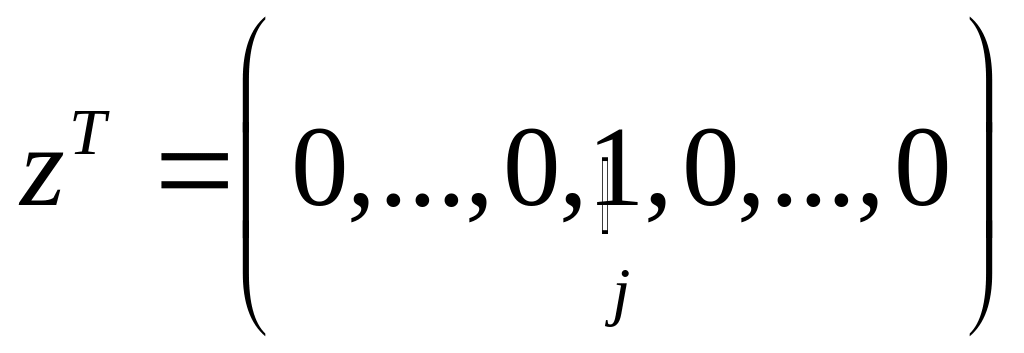, то , тобто всі діагональні елементи матриці є від’ємними.