Концептуальна модель односекторної економіки. Неокласичні макровиробничі функції.
Під односекторною однопродуктовою економікою будемо розуміти економіку (як цілісну систему), яка виробляє єдиний універсальний продукт, який може як споживатись, так й інвестуватись. Концептуальна схема (модель) такої економіки наведена нище:
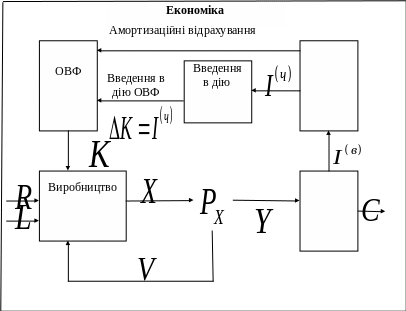
Прийняті
такі позначення:
– природні ресурси,
– трудові ресурси (кількість зайнятих
працівників),
– засоби праці або ОВФ,
– валовий випуск,
– виробниче споживання (проміжна
продукція),
– блок розподілу валового випуску,
– ВВП (кінцева продукція),
– блок розподілу ВВП,
– невиробниче споживання (фонд
невиробничого споживання),
– валові капітальні вкладення (валові
інвестиції),
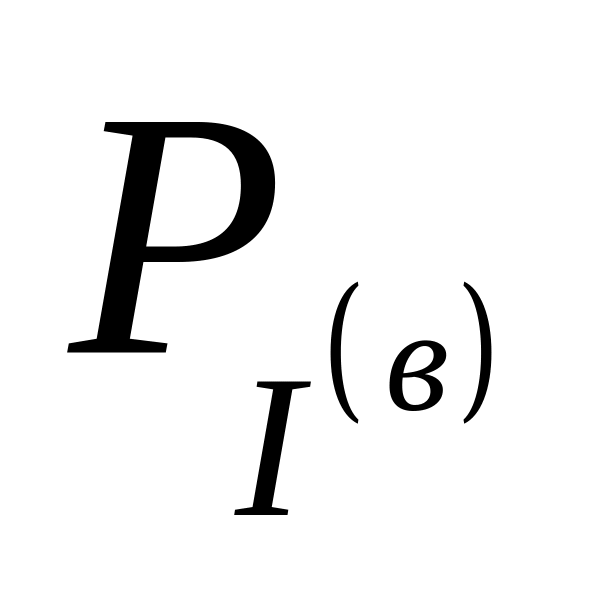– блок розподілу валових капітальних
вкладень,
– чисті капітальні вкладення (чисті
інвестиції),
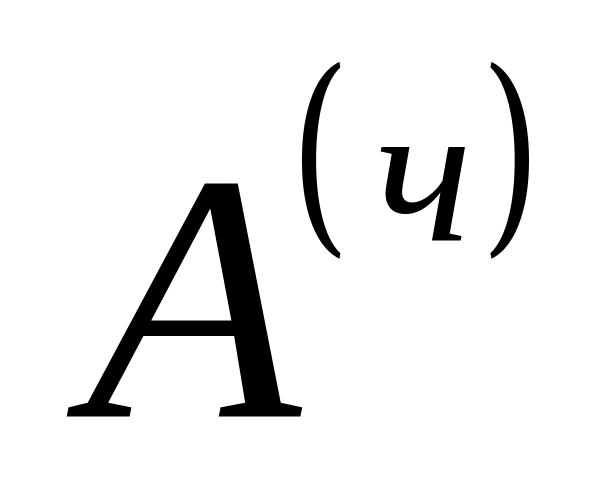– амортизаційні відрахування,
– приріст ОВФ (
).
З даної концептуальної моделі випливають такі базові співвідношення:
, (6.1)
,
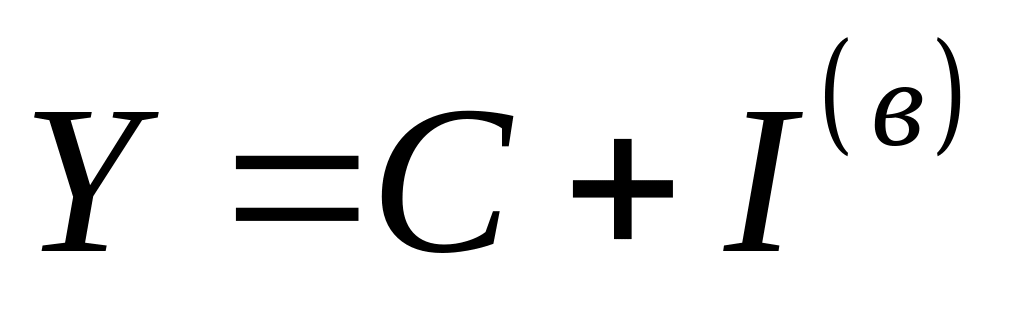(6.2)
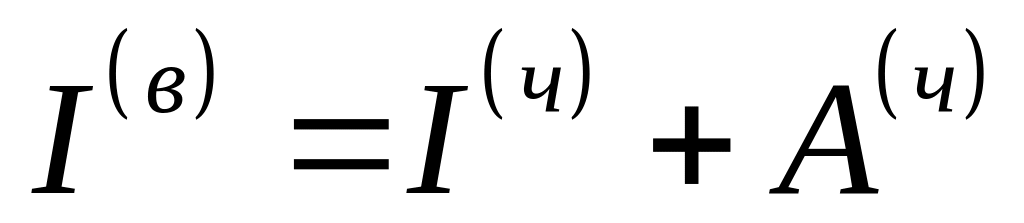. (6.3)
Зміст рівностей (6.1)–(6.3) очевидний. Не зупиняючись на деталізації (6.1)–(6.3), зазначимо лише, що вони є основою для побудови математичних моделей економічного росту, до яких ми повернемося пізніше.
МВФ – це функції, які є моделями або під моделями процесів та систем на макрорівні. Отже, надалі будемо мати справу з МВФ
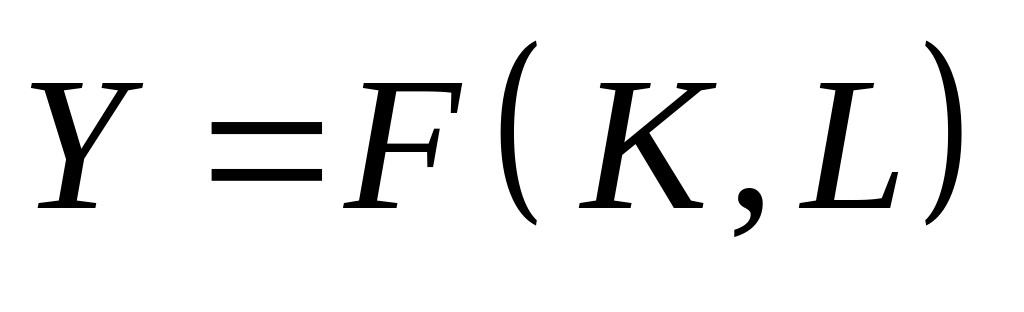. (6.4)
Функція (6.4) називається неокласичною МВФ, якщо вона двічі неперервно диференційовна та задовольняє наступні властивості:
1)
(6.5)
– за відсутності хоча б одного ресурсу виробництво неможливе;
2)
,
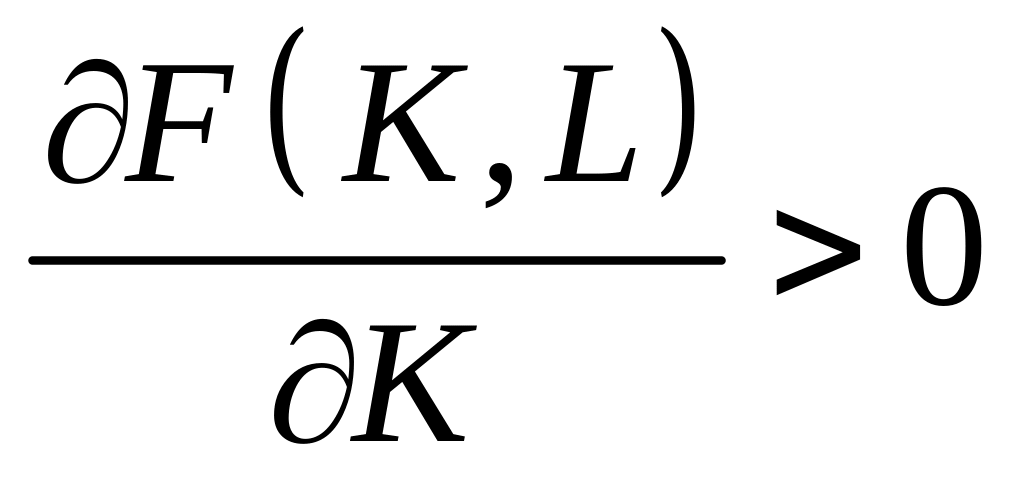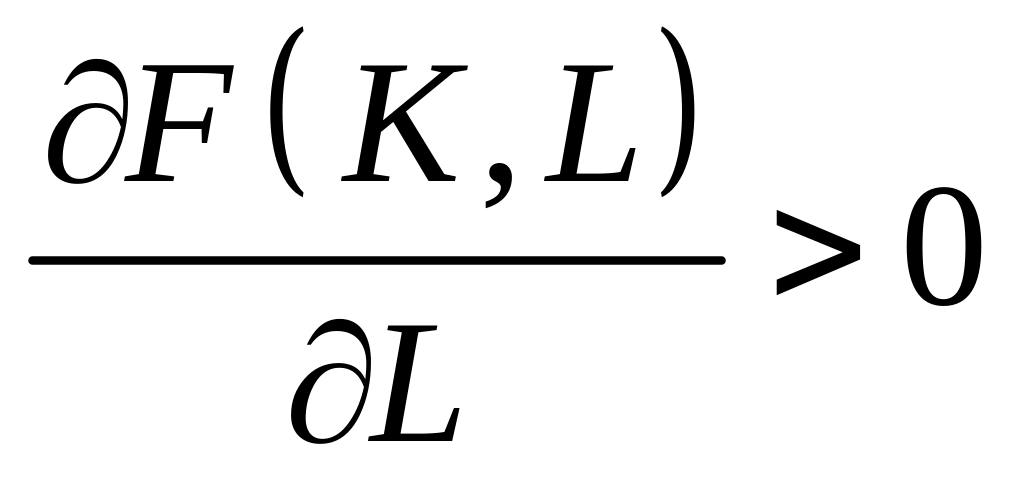(6.6)
– збільшення витрат виробничих фондів і робочої сили призводить до зростання випуску продукції;
3)
,
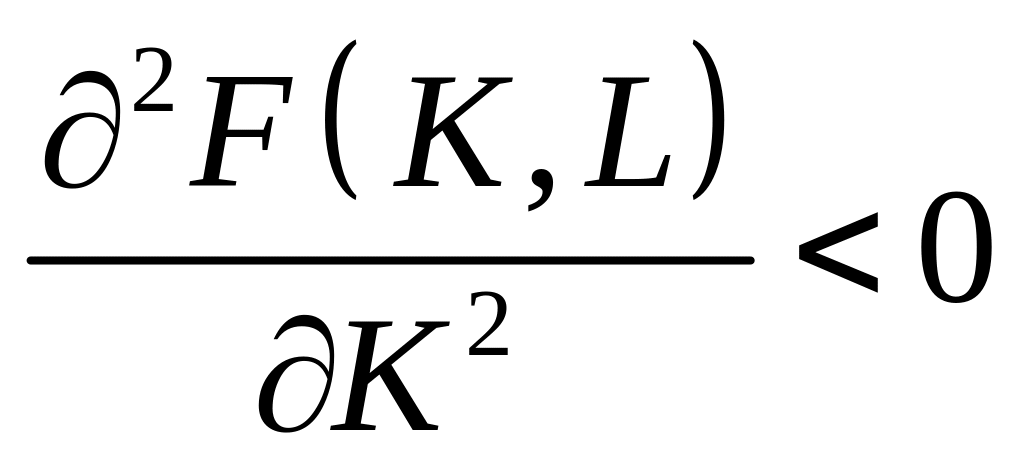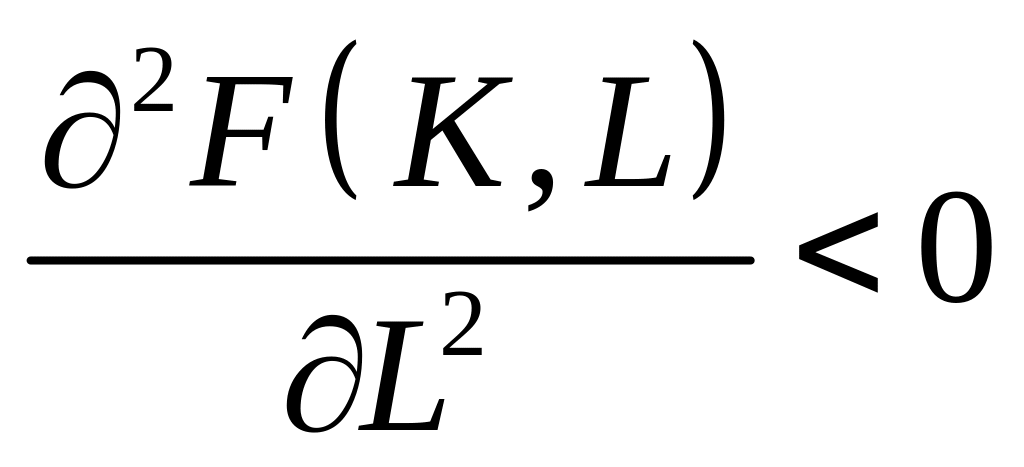(6.7)
– в умовах екстенсивного розвитку економіки збільшення витрат лише одного виробничого ресурсу ( або ) призводить до падіння ефективності його використання;
4)
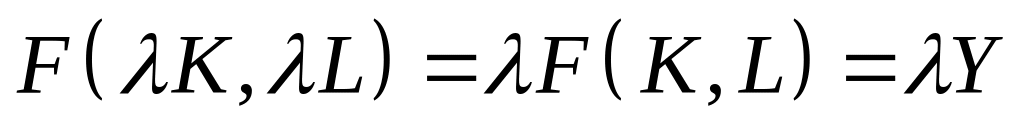(6.8)
– обсяг випуску
характеризується постійною віддачею
від розширення масштабів виробництва
;
5)
,
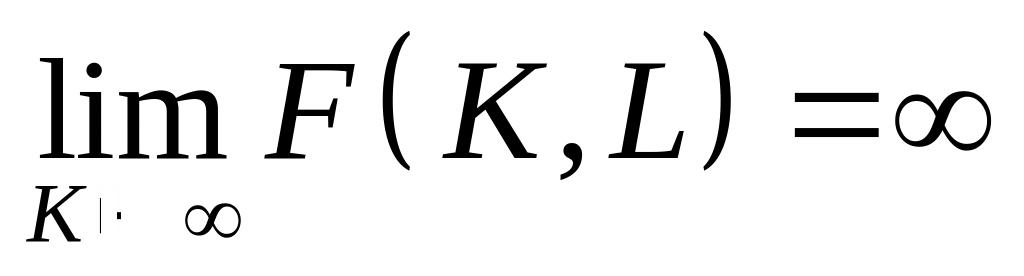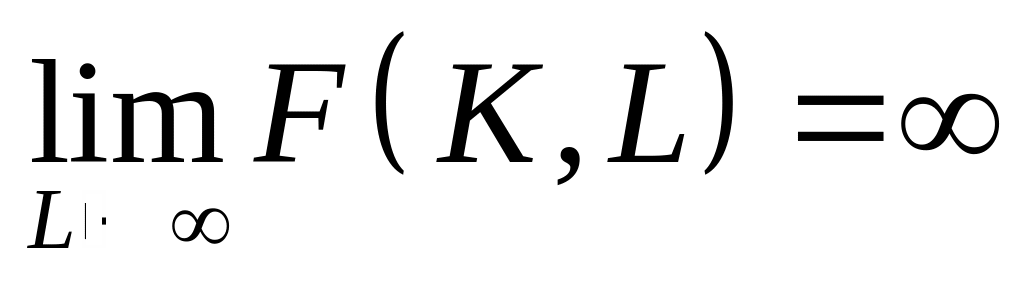(6.9)
– при необмеженому зростанні одного з ресурсів випуск необмежено зростає;
6)
,
,
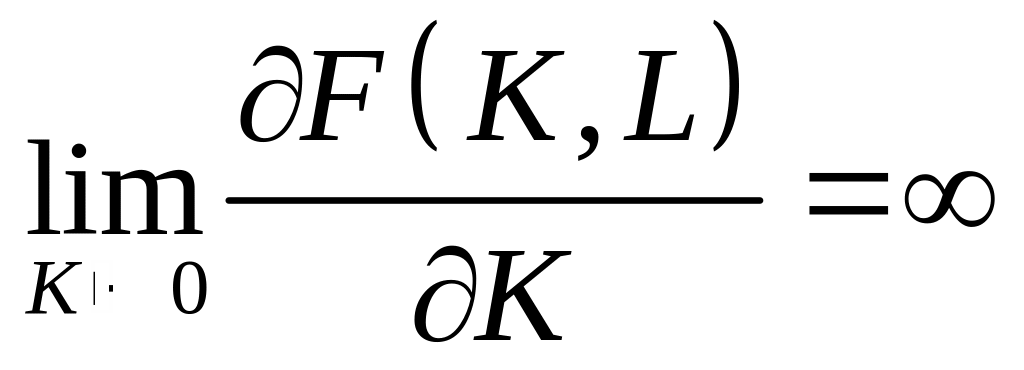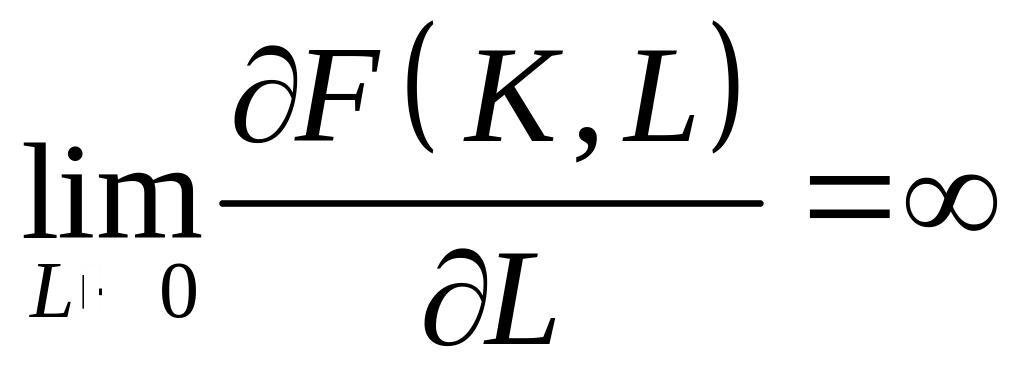(6.10)
,
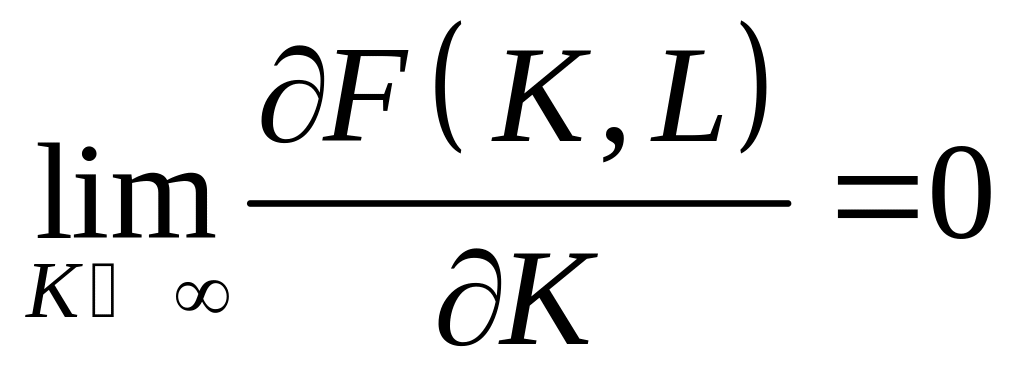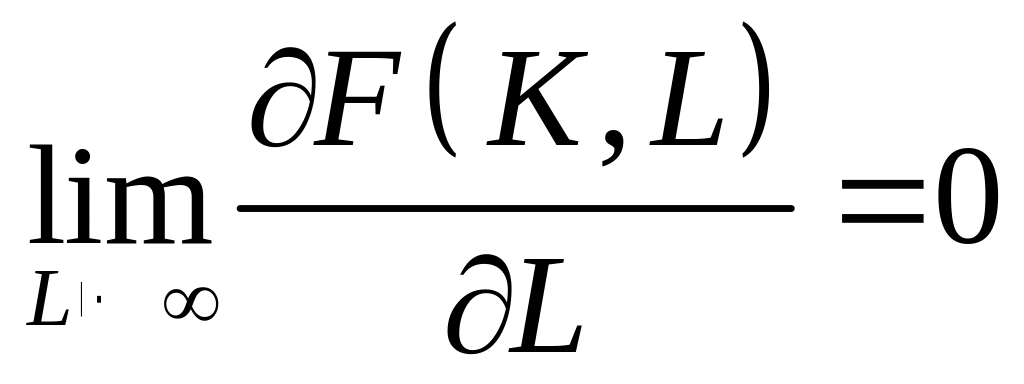(6.11)
– граничні ефективності фондів та праці необмежено зростають при наближенні відповідних ресурсів до нуля та спадають до нуля при необмеженому зростанні ресурсів.
Стосовно умов (6.7) варто сказати, що дуже часто вони підсилюються аксіомою угнутості чи строгої угнутості МВФ у цілому.
Інколи до макровиробничої функції вводиться змінна часу , щоб урахувати ряд зовнішніх факторів, зокрема вплив науково-технічного прогресу. Але тут МВФ, що явно залежить від , розглядати не будемо.
Зручність функції (6.4), що задовольняє властивості (6.5)–(6.11), полягає перш за все в тому, що ми можемо замінити її однофакторним еквівалентом, тобто функцією
,
(6.12)
де
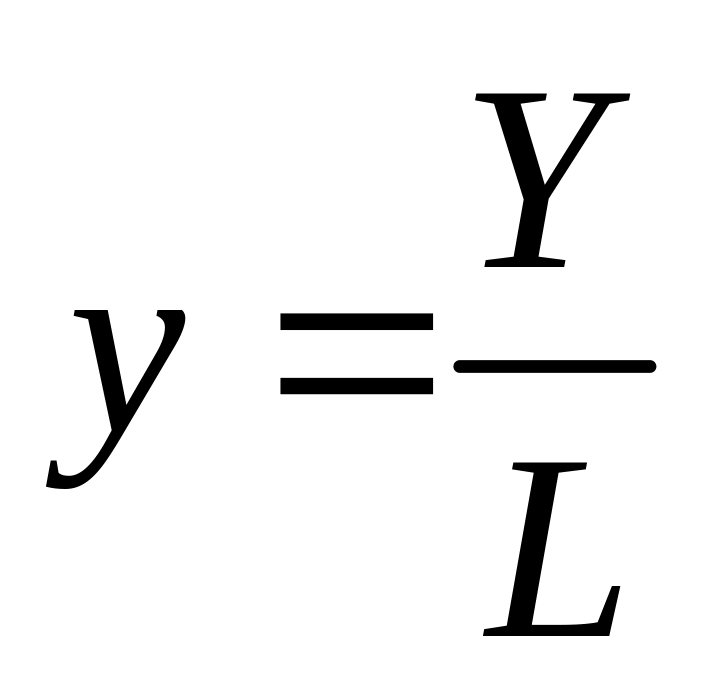– середня продуктивність праці,
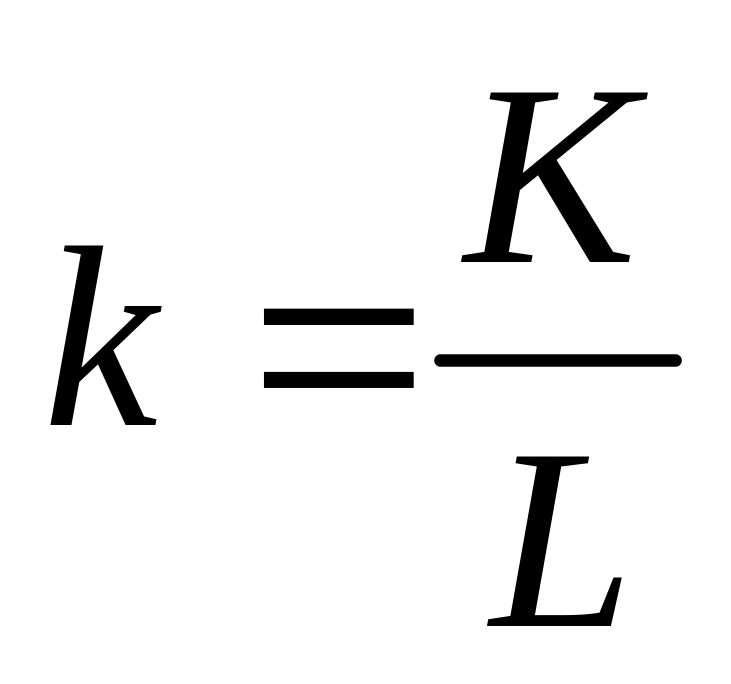– капіталоозброєність (або фондоозброєність),
.
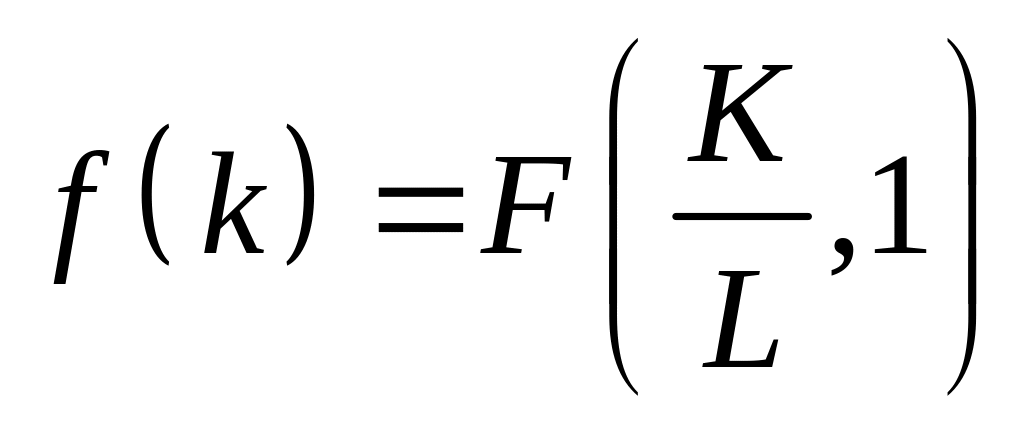На основі (6.5)–(6.11) легко встановити, що для функції (6.12) виконуються такі умови:
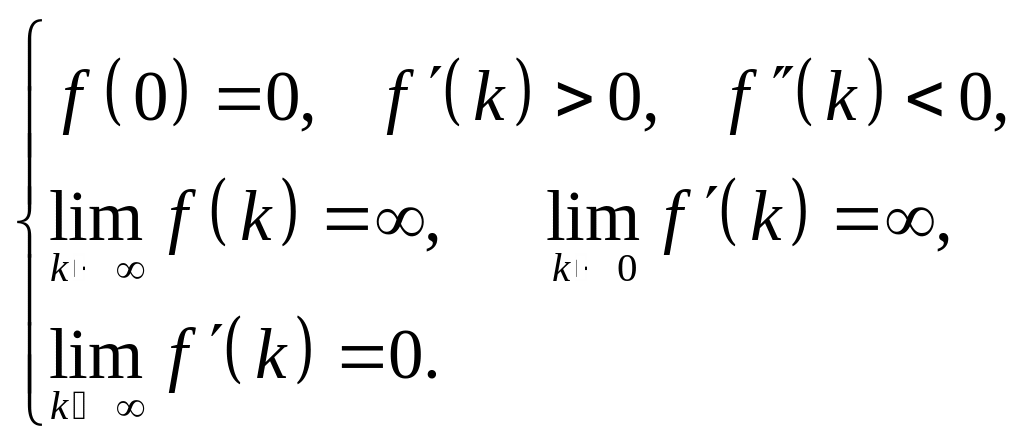(6.13)
Двічі неперервно диференційовна функція (6.12), що задовольняє обмеження (6.13), називається однофакторною неокласичною виробничою функцією.