Стохастичний аналог моделі Леонтьєва.
Розглянута раніше модель Леонтьєва є статичною, однозначно визначеною. На практиці в більшості випадків матриця А є продуктивною, тобто не виникає проблем із знаходженням розв’язку моделі Леонтьєва, який у матричному вигляді записується так:
Як
правило, модель Леонтьєва (5.7)
використовується для прогнозування
вектора валового випуску
при заданому векторі кінцевої продукції
.
Проблема існування шуканого вектора
,
тобто проблема продуктивності моделі,
є основною при розв’язанні цієї задачі.
У більшості випадків реальна матриця
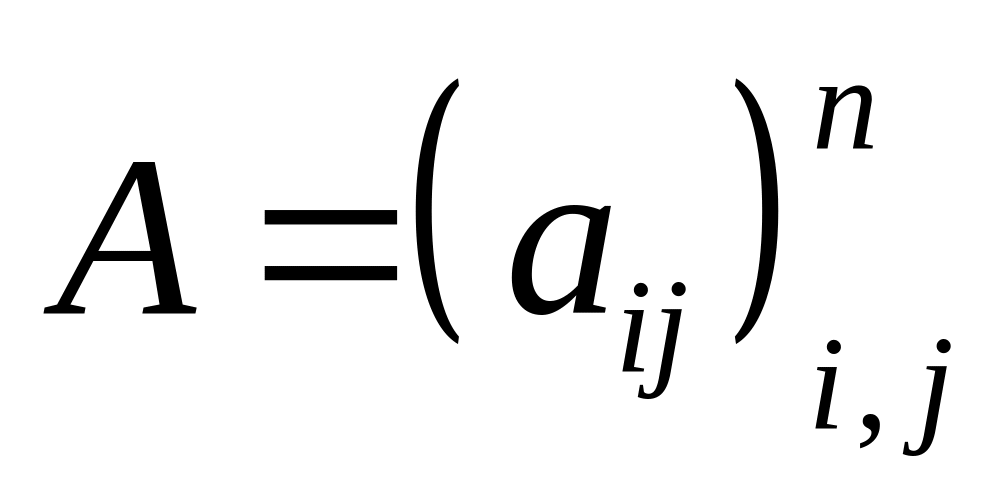така, що
,
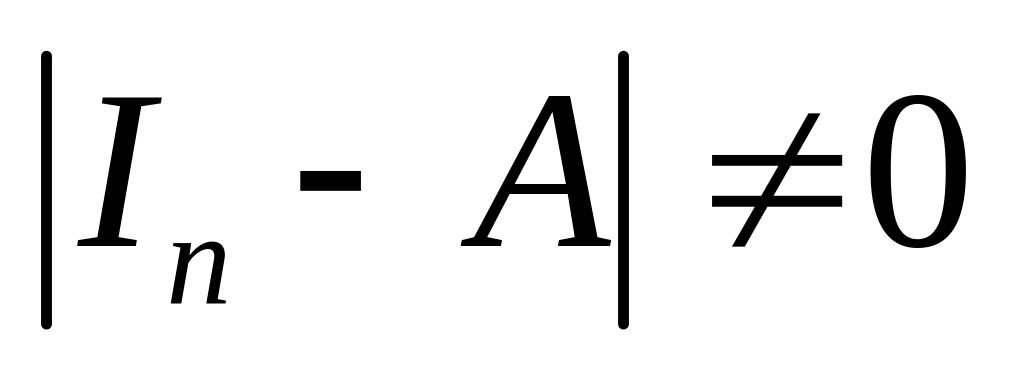тому існування єдиного невід’ємного
розв’язку
системи (5.7) (чи (5.6)) забезпечується
невід’ємністю матриці
.
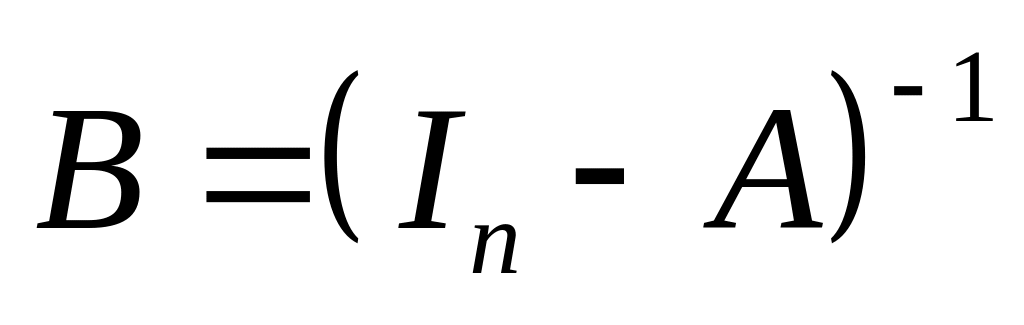Ситуація
змінюється, якщо матрицю
вважати випадковою (внаслідок помилок
вимірювання та прогнозування), тобто
вважати, що кожний її елемент
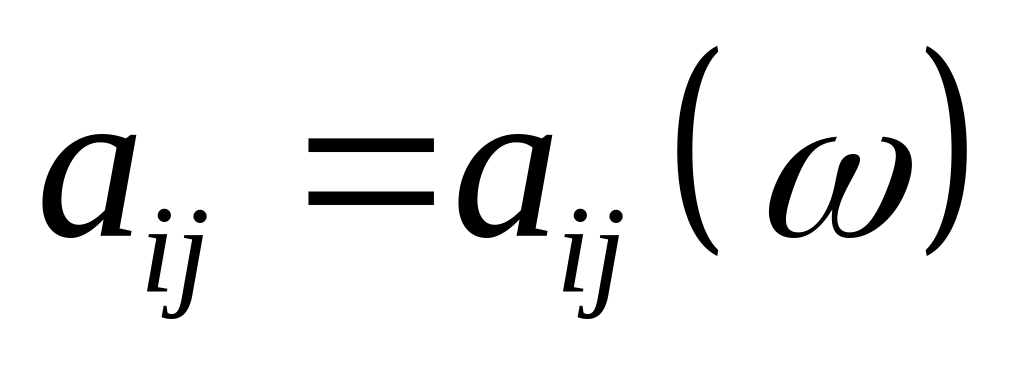є випадковою величиною або дійсною
числовою функцією, заданою на множині
елементарних подій
,
яка є елементом імовірнісного простору
,
де
–
так звана
– алгебра подій, а
– імовірнісна міра, визначена на
і
(згідно з визначенням випадкової величини
для будь-якого
,
виконується умова
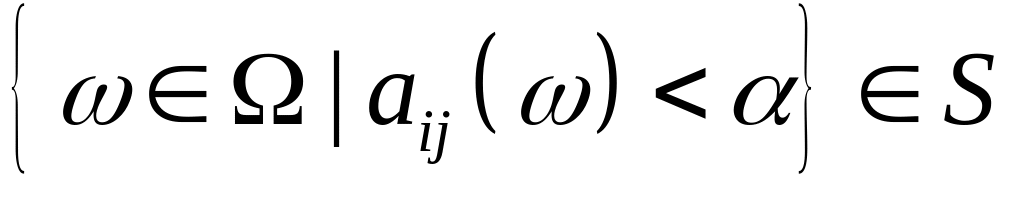та існує ймовірність
,
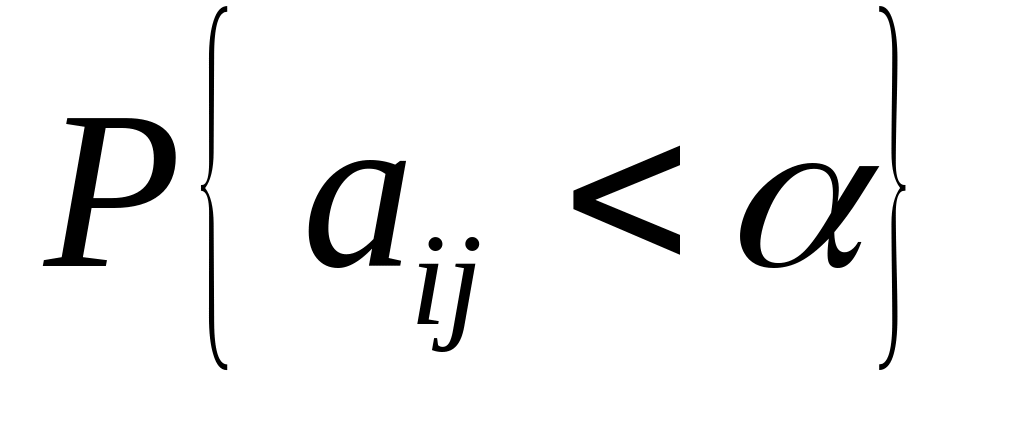яка дорівнює конкретному значенню
функції розподілу
,
).
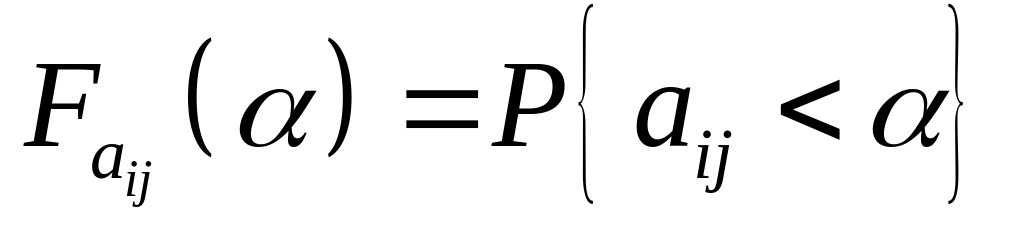Якщо матриця прямих матеріальних витрат
випадкова, то реальний випуск кінцевої
продукції
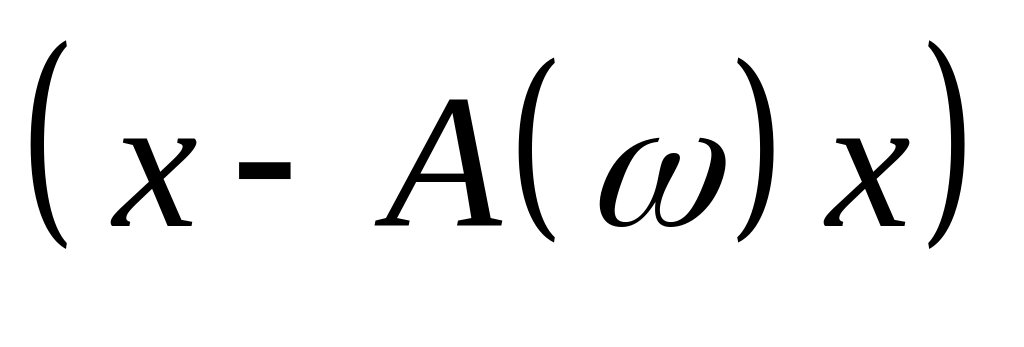буде випадковим вектором і лише в
рідкісних випадках він може збігатись
із плановим вектором
(для детермінованого випадку
),
тому досягти балансу в традиційному
розумінні неможливо. Це означає, що
випуск валової продукції потрібно
вибирати так, щоб мінімізувати похибку
апріорного відхилення. Реалізувати цей
вибір можна, наприклад, мінімізуючи
математичне сподівання суми квадратів
відхилень, тобто розв’язуючи задачу
стохастичного програмування
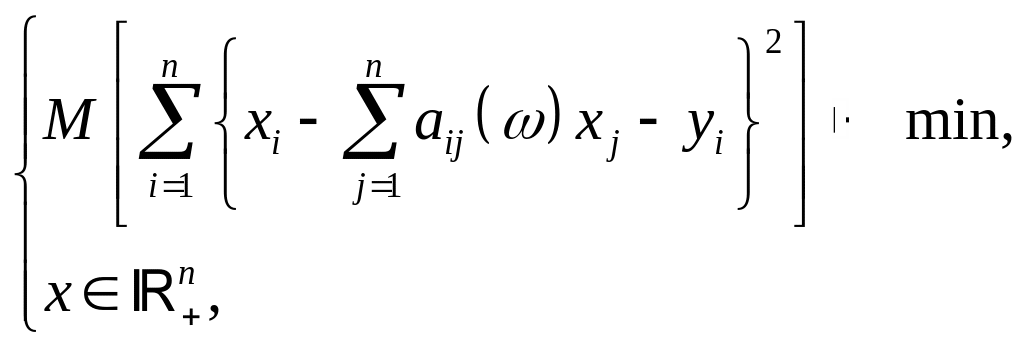(5.35)
де
– математичне сподівання. Задача (5.35)
є задачею стохастичного програмування
в так званій
-постановці,
при якій випадкова величина замінюється
її математичним сподіванням, і задача
зводиться до оптимізації детермінованої
цільової функції. Не
зупиняючись на методах розв’язування
задачі (5.35), зазначимо лише, що вона
формалізує один із можливих стохастичних
аналогів моделі Леонтьєва [5, 19, 23].
Стосовно (5.35) вводиться також поняття
стохастичної продуктивності.
Означення
5.4.
Модель (5.35) називається стохастично
продуктивною, якщо вона має розв’язок
при будь-якому
.
З поняттям
стохастичної продуктивності тісно
зв’язано поняття повних стохастичних
витрат валової продукції (в детерміновану
випадку такий зв’язок є між продуктивністю
та повними витратами валової продукції).
Якщо вектор
в задачі (5.35) є сукупністю параметрів,
то її розв’язок буде вектор-функцією
.
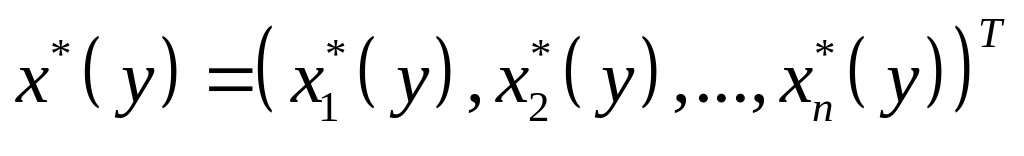Означення 5.5. Якщо існують похідні , то матриця
,
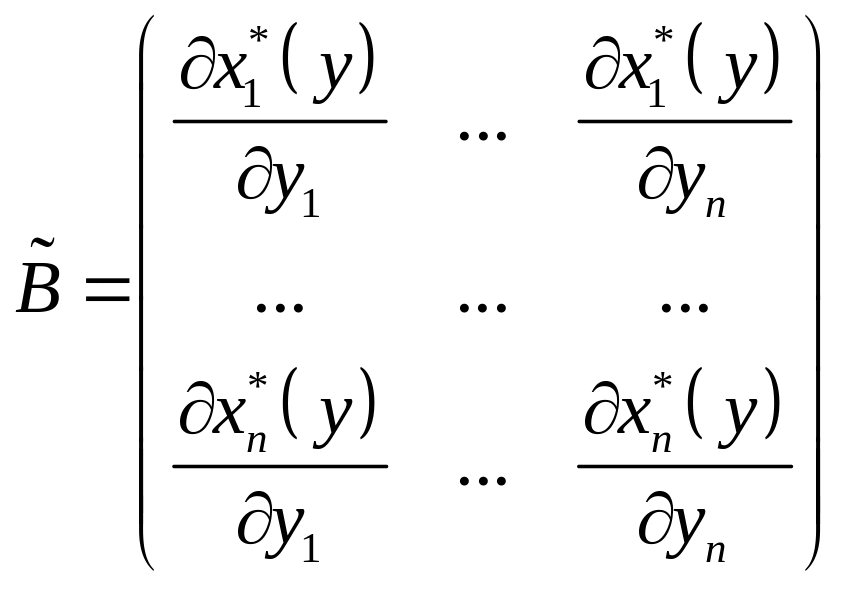називається матрицею повних стохастичних витрат.
Наступні
твердження дають прості достатні умови
існування матриці
і критерій стохастичної продуктивності
стохастичного аналога моделі Леонтьєва.
Теорема 5.12 (про існування матриці повних стохастичних витрат для моделі (5.35)). Якщо
,
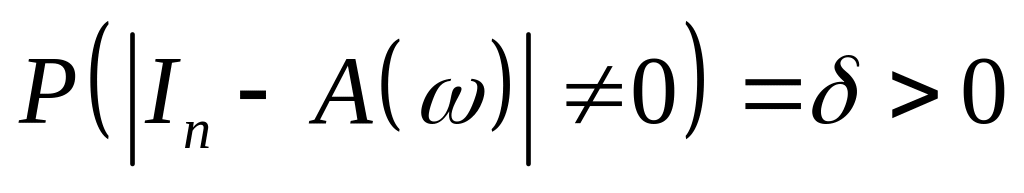то матриця повних стохастичних витрат існує.
Теорема 5.13 (критерій стохастичної продуктивності моделі (5.35)). Щоб модель (5.35) була стохастично продуктивною, необхідно й достатньо, щоб її матриця повних стохастичних витрат була невід’ємною.
Більш
детальне дослідження моделі (5.35) можна
знайти у [23, 46].
Зауважимо лише, що модель (5.35) для реальних
матриць
,
як правило, є стохастично продуктивною.
Крім моделі (5.35), можна запропонувати також інші варіанти стохастичних аналогів моделі Леонтьєва. Однак навіть цієї моделі достатньо для ілюстрації стохастичного підходу в моделюванні міжгалузевих (чи інших внутрісистемних) балансових співвідношень і з’ясування деяких проблем, пов’язаних зі стохастичною інформацією.