
- •Простір товарів та відношення переваги. Поняття функції корисності, теорема Дебре. Неокласичні функції корисності, їх властивості та характеристики.
- •Неокласична модель поведінки споживача.
- •Функції попиту та граничної вартості грошей.
- •Рівняння Слуцького у векторній та матричній формі. Матриця Слуцького і її властивості.
- •Класифікація товарів на основы функцій попиту на товари.
- •Еластичність попиту та умови агрегації.
- •Поняття виробничої функції. Класифікація та сфера застосування виробничих функцій.
- •Найпростіші моделі поведінки виробників: моделі максимізації прибутку та випуску продукції
- •Функції попиту на ресурси та пропозиції випуску.
- •Порівняльна статика фірми. Основне матричне рівняння теорії фірми.
- •Аналіз чутливості функцій попиту та пропозиції до змін цінових параметрів.
- •Неокласичні моделі багатопродуктової фірми в умовах досконалої конкуренції.
- •Моделі однопродуктової фірми в умовах недосконалої конкуренції (монополія, монопсонія).
- •Моделі однопродуктової фірми в умовах недосконалої конкуренції (олігополія, олігопсонія). Рівновага за Курно. Рівновага та нерівновага за Стакельбергом.
- •Моделі встановлення рівноважної ціни: павутиноподібна модель, моделі Еванса та Самуельсона.
- •Класична модель загальної економічної рівноваги
- •Поняття загальної економічної рівноваги. Модель Вальраса.
- •Коефіцієнт трудових витрат і витрат виробничих фондів
- •Порівняльна статика моделі Леонтьєва.
- •Стохастичний аналог моделі Леонтьєва.
- •Означення 5.5. Якщо існують похідні , то матриця
- •Динамічна модель міжгалузевого балансу.
- •Аналіз оптимальних траєкторій динамічної моделі Леонтьєва засобами магістральної теорії.
- •Модель Неймана. Поняття динамічної рівноваги, продуктивності й нерозкладності для моделі Неймана.
- •Концептуальна модель односекторної економіки. Неокласичні макровиробничі функції.
- •26. Модель оптимального економічного росту рамсеївського типу.
- •6.3.1. Деякі варіанти моделі Рамсея
Простір товарів та відношення переваги. Поняття функції корисності, теорема Дебре. Неокласичні функції корисності, їх властивості та характеристики.
Теорія споживання – це теорія раціональної поведінки споживача на ринку товарів.
Споживач – це окремий індивідум або група індивідумів, що спільно розподіляють свій дохід на закупівлю товарів, а товар – це споживче благо або послуга, що надійшли у продаж в певний час і в певному місці.
Означення
1.1.
Множина
![]() всіх мислимих наборів товарів, доступних
і придатних для споживача, називається
простором товарів.
всіх мислимих наборів товарів, доступних
і придатних для споживача, називається
простором товарів.
В
математичній теорії споживання кожний
набір товарів асоціюється з деяким
вектором (точкою) простору
![]() ,
тобто
,
тобто
![]() .
Основна проблема споживача полягає в
тому, що він повинен вміти порівнювати
довільних два набори товарів
.
Основна проблема споживача полягає в
тому, що він повинен вміти порівнювати
довільних два набори товарів
![]() і зробити з них вибір. Вибір, звичайно,
залежить від смаку споживача, його
бюджету та цін на товари. Спочатку
розглянемо поведінку споживача на ринку
товарів, який не зв’язаний з бюджетним
обмеженням. В математичному плані це
означає, що потрібно вибрати такий
математичний апарат, за допомогою якого
можна ввести операцію порівняння двох
довільних наборів товарів
.
і зробити з них вибір. Вибір, звичайно,
залежить від смаку споживача, його
бюджету та цін на товари. Спочатку
розглянемо поведінку споживача на ринку
товарів, який не зв’язаний з бюджетним
обмеженням. В математичному плані це
означає, що потрібно вибрати такий
математичний апарат, за допомогою якого
можна ввести операцію порівняння двох
довільних наборів товарів
.
Такий апарат базується на теорії порівняльних переваг.
Виділяють такі основні пріоритетні відношення переваги:
 – не
гірше, ніж;
– не
гірше, ніж; – краще,
ніж;
– краще,
ніж; – рівноцінно.
– рівноцінно.
Інакше кажучи, перші два відношення переваги є відношеннями нестрогої і строгої переваги, а останнє – відношенням байдужості (нейтральності).
Запис
![]() означає, що споживач віддає перевагу
набору товарів
означає, що споживач віддає перевагу
набору товарів
![]() перед набором товарів
перед набором товарів
![]() або не робить між ними ніякої різниці
або не робить між ними ніякої різниці
![]() .
Крім того, відношення
.
Крім того, відношення
![]() рівносильне тому, що
,
але відношення
рівносильне тому, що
,
але відношення
![]() не має місця.
не має місця.
Відношення
![]() рівносильне тому, що
і
одночасно.
рівносильне тому, що
і
одночасно.
Конкретизуємо основні аксіоми відношення переваги.
Аксіома
1.1.
Відношення
переваги
є рефлексивним, тобто
![]() для всіх
для всіх
![]() .
.
Аксіома
1.2.
Відношення переваги
є транзитивним, тобто з того, що
і
![]() випливає, що
випливає, що
![]() для всіх
для всіх
![]() .
.
Аксіома 1.3. Для будь-якої пари наборів товарів або або .
Аксіома
1.4.
Відношення переваги
є неперервним, тобто множина
![]() є відкритою у декартовому добутку
є відкритою у декартовому добутку
![]() .
.
Аксіома
1.5.
Відношення переваги
є монотонним, тобто з того, що
![]() випливає, що
випливає, що
![]() .
.
Зазначимо,
що аксіоми 1-3 є зрозумілими і не потребують
додаткових пояснень. Четверта аксіома
означає, що коли споживач віддає перевагу
набору
![]() перед набором
перед набором
![]() ,
то він обов’язково віддасть перевагу
набору
перед набором
,
то він обов’язково віддасть перевагу
набору
перед набором
![]() ,
якщо
і
відповідно близькі до
і
.
П’ята аксіома стверджує, що споживач
буде надавати перевагу більшій кількості
товарів.
,
якщо
і
відповідно близькі до
і
.
П’ята аксіома стверджує, що споживач
буде надавати перевагу більшій кількості
товарів.
Введемо також ряд важливих понять.
Означення
1.2.
Пару
![]() ,
тобто простір товарів з відношенням
переваги
певного споживача, називають полем
переваг цього споживача.
,
тобто простір товарів з відношенням
переваги
певного споживача, називають полем
переваг цього споживача.
Означення
1.3.
Переважаючою
множиною відносно набору товарів
![]() називається множина
називається множина
![]() .
.
Означення
1.4.
Непереважаючою
множиною відносно набору
називається множина
![]() .
.
Означення
1.5.
Множина спільних для множин
![]() і
і
![]() граничних точок називається класом
байдужості
граничних точок називається класом
байдужості
![]() .
.
Сукупність
класів байдужості утворює так званий
фактор – простір
![]() простору
.
Якщо
– зв’язна множина, то при
простору
.
Якщо
– зв’язна множина, то при
![]() клас байдужості утворює криві байдужості,
при
клас байдужості утворює криві байдужості,
при
![]() – поверхні байдужості, при
– поверхні байдужості, при
![]() – гіперповерхні байдужості.
– гіперповерхні байдужості.
Означення
1.6.
Нехай
– поле переваг, а
![]() – деяка підмножина. Елемент
– деяка підмножина. Елемент
![]() називається найбільш (найменш) переважаючим
в
називається найбільш (найменш) переважаючим
в
![]() ,
якщо
,
якщо
![]() для всіх
для всіх
![]() .
.
Простір товарів , доступний і придатний споживачеві, може і не мати найбільш переважаючого елемента.
Означення 1.7. Для поля переваг найбільш переважаючий елемент називається точкою насичення. Якщо не має точки насичення, то має місце ненасичуваність.
Поняття функції корисності. Теорема Дебре.
Нехай, як і раніше, – деяке поле переваг споживача, причому відношення переваги „ ” задовольняє переліченим вище аксіомам.
Означення
1.8.
Визначена
на множині
числова функція
![]() називається індикатором переваги
або функцією корисності, що відображає
відношення переваги
,
якщо для всіх
називається індикатором переваги
або функцією корисності, що відображає
відношення переваги
,
якщо для всіх
![]() тоді і лише тоді, коли
тоді і лише тоді, коли
![]()
Інакше
кажучи, функція
![]() є числовим втіленням порядкової структури
поля переваг. Використовуючи дане
означення та згадані вище аксіоми,
встановлюються такі властивості:
є числовим втіленням порядкової структури
поля переваг. Використовуючи дане
означення та згадані вище аксіоми,
встановлюються такі властивості:
для довільних
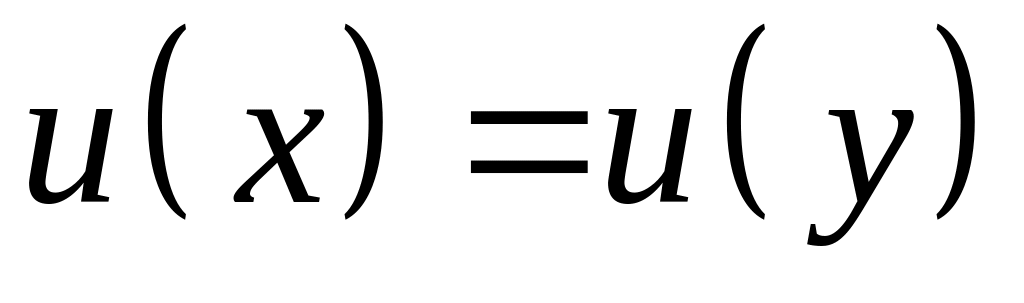 тоді і лише тоді, коли
,
тобто множини рівнів функції корисності
збігаються з класами байдужості для
відношення переваги
;
тоді і лише тоді, коли
,
тобто множини рівнів функції корисності
збігаються з класами байдужості для
відношення переваги
;якщо для поля переваг існує принаймні одна функція корисності, то існує також безліч функцій корисності, які одержуються одна з одної за допомогою строго монотонно зростаючих перетворень (з точністю до цих перетворень функція корисності є єдиною для поля переваг );
функція корисності буде монотонною (тобто якщо
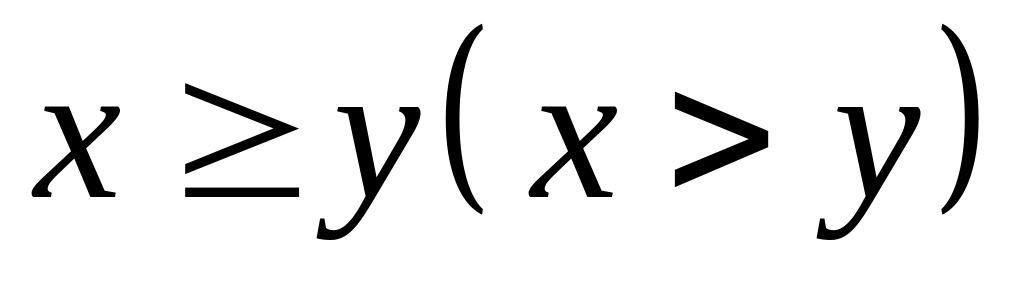 ,
то
,
то
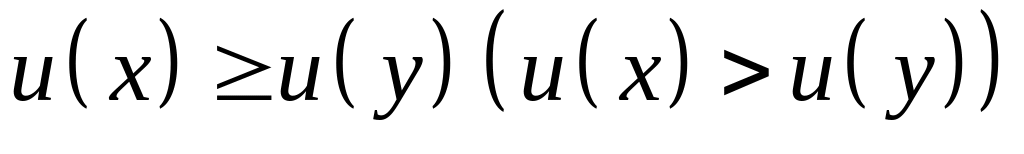 тоді і лише тоді, коли відношення
переваги
буде монотонним;
тоді і лише тоді, коли відношення
переваги
буде монотонним;функція корисності є квазіугнутою (тобто для довільного
 множина
множина
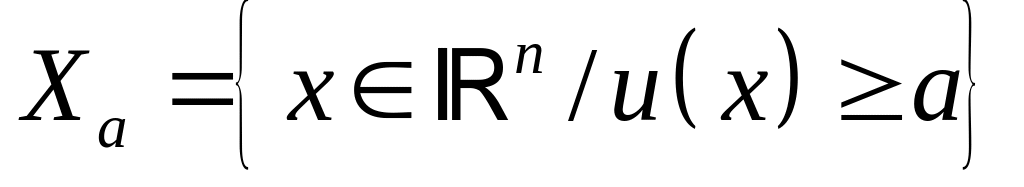 є опуклою) тоді і лише тоді, коли
відношення переваги
є опуклим (із того, що
для
випливає, що
є опуклою) тоді і лише тоді, коли
відношення переваги
є опуклим (із того, що
для
випливає, що
 ).
).
Всі ці властивості є важливими з позицій обґрунтування конкретних класів функцій корисності та їх використання на практиці.
Одним з центральних результатів сучасної теорії споживання і теорії корисності є теорема Ж.Дебре.
Теорема 1.1. (Теорема Дебре) Якщо множина є зв’язною, а відношення переваги неперервним, то функція корисності для поля переваг існує.
Доведення цієї теореми в загальному випадку є досить складним і громіздким. Відзначимо лише те, що теорема Дебре вирішує принципову проблему – проблему існування числової функції в полі переваг споживача, тобто функції корисності (Ж.Дебре – відомий американський економіст-математик, лауреат Нобелівської премії з економіки (1983р.) за розробки з теорії загальної економічної рівноваги).
Неокласичні функції корисності.
В полі переваг , для якого відношення переваги є опуклим, функція корисності (як випливає з попереднього пункту) буде квазіугнутою (квазіопуклою вгору). Однак, квазіугнуті функції є незручними для роботи. Вони утворюють занадто великий клас для того, щоб успішно застосовувати їх на практиці. Значно зручніше працювати з угнутими або строго угнутими функціями (кожна угнута функція є квазіугнутою, але не навпаки).
Надалі розглянемо клас строго угнутих і двічі неперервно диференційовних функцій корисності, які утворюють підклас так званих неокласичних функцій корисності. Ці функції мають такі властивості:
1)
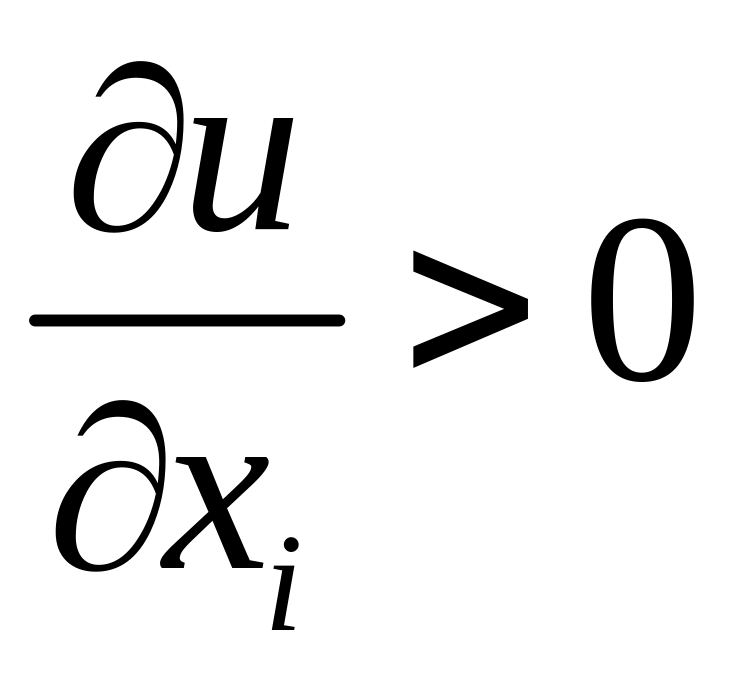 – ріст споживчого блага приводить до
зростання корисності;
– ріст споживчого блага приводить до
зростання корисності;
2)
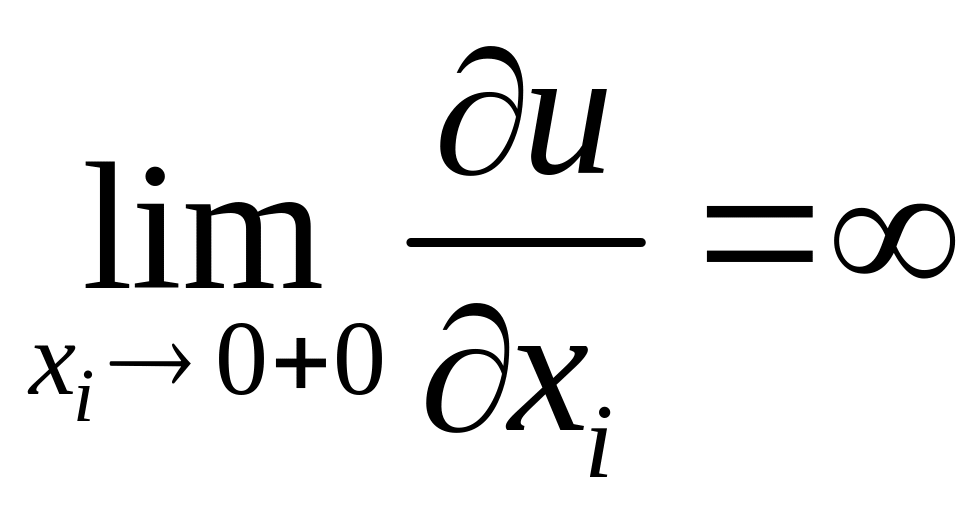 – невеликий приріст блага за його
початкової відсутності різко збільшує
корисність;
– невеликий приріст блага за його
початкової відсутності різко збільшує
корисність;
3)
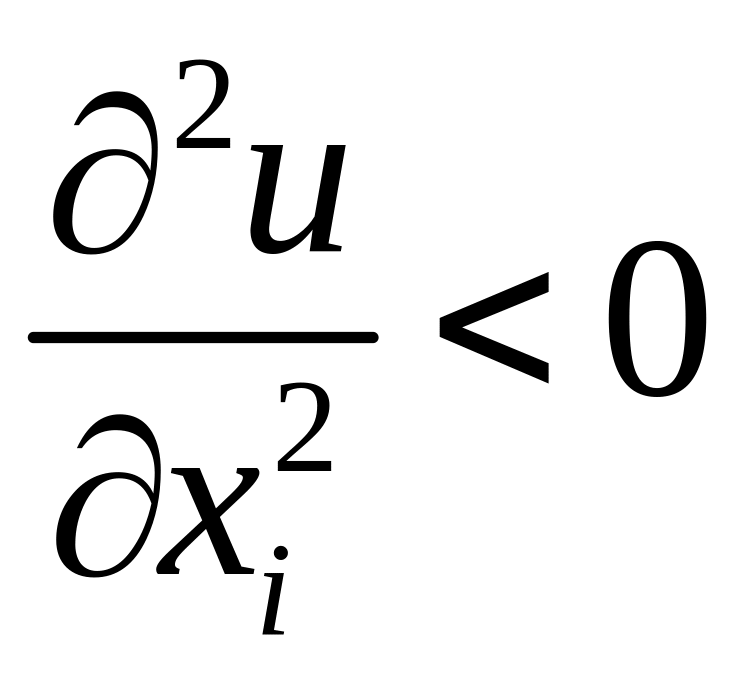 – ефективність (швидкість зростання)
корисності зменшується із зростанням
споживчого блага;
– ефективність (швидкість зростання)
корисності зменшується із зростанням
споживчого блага;
4)
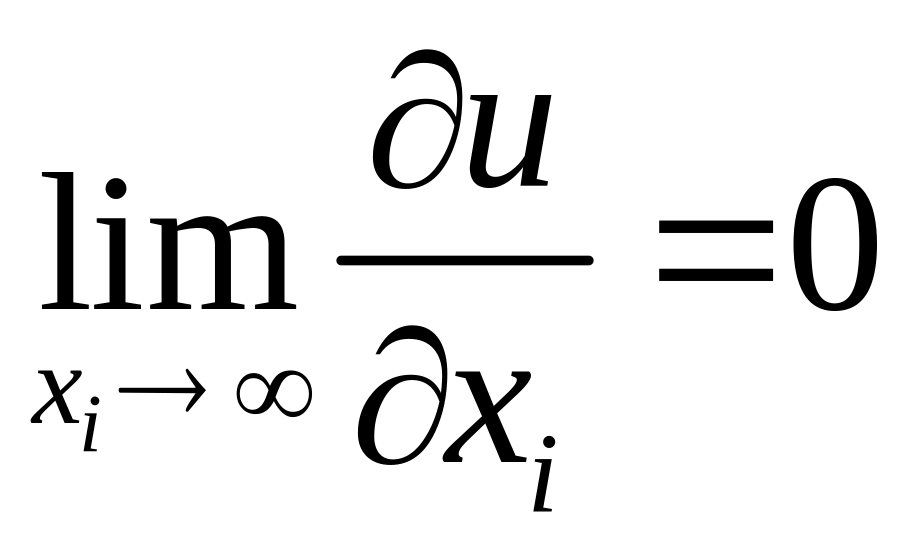 – при дуже великому обсязі споживчого
блага його подальше зростання не
приводить до зростання корисності.
– при дуже великому обсязі споживчого
блага його подальше зростання не
приводить до зростання корисності.
Зазначимо, що умова 3), як правило, замінюється більш сильною умовою: матриця других похідних (матриця Гессе)
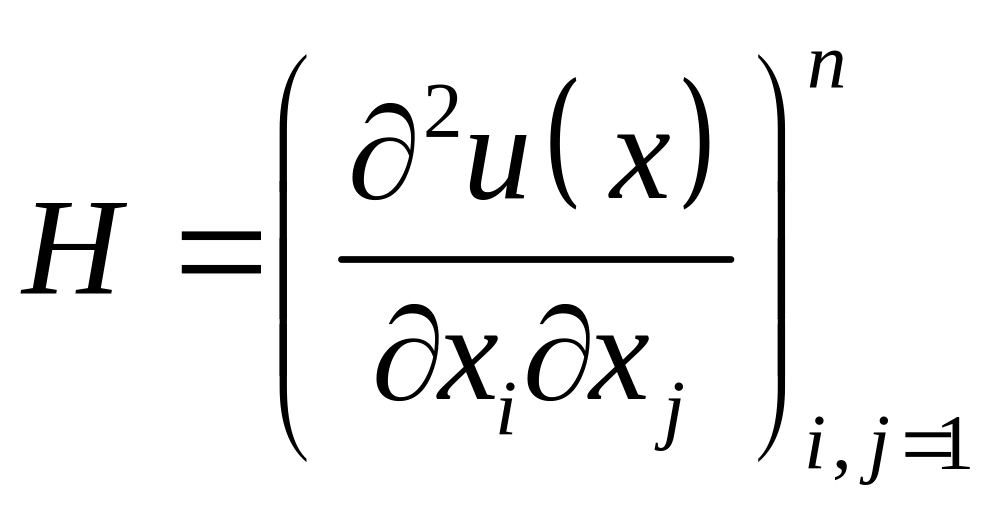
є від’ємно визначеною.
Крім того, умова 3) моделює так званий перший закон Госсена (Х.Госсен (1810-1858) – німецький економіст, що займався теорією корисності): гранична корисність будь-якого товару зменшується зі збільшенням споживання цього товару.
Поверхнею
байдужості
називається гіперповерхня розмірності
![]() ,
на якій корисність є постійною
,
на якій корисність є постійною
![]()
В диференціальній формі останнє співвідношення записується так:
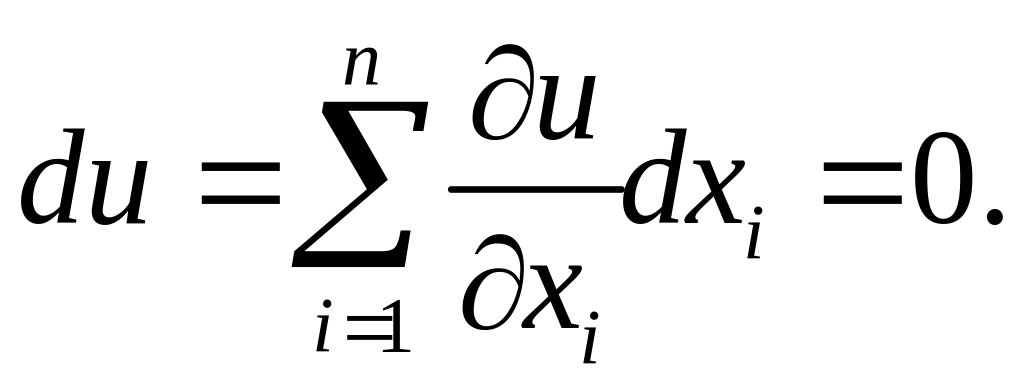 (1.1)
(1.1)
Умова
(1.1) означає, що
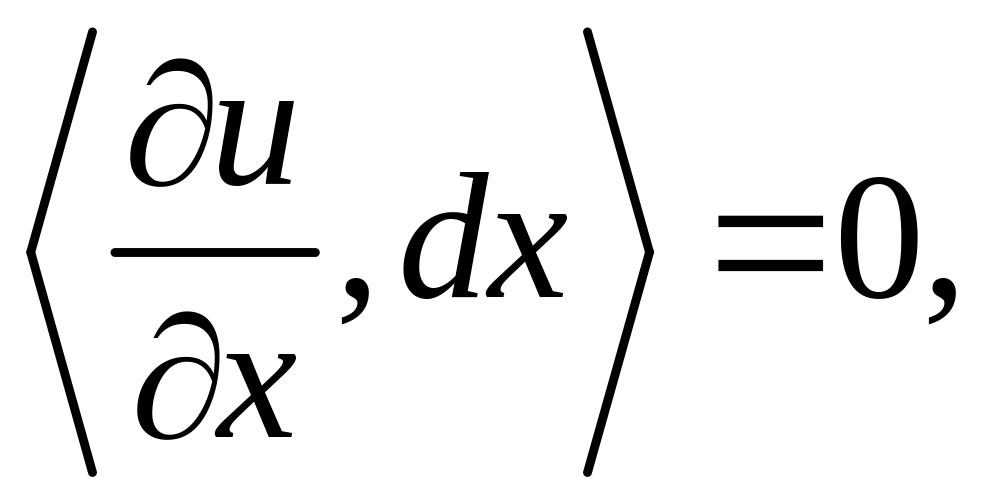 тобто дотична до поверхні байдужості
перпендикулярна градієнтові функції
корисності (
тобто дотична до поверхні байдужості
перпендикулярна градієнтові функції
корисності (![]() – операція скалярного добутку).
– операція скалярного добутку).
Уточнимо
деякі числові характеристики неокласичної
функції корисності. До них належать
середня
![]() та гранична
та гранична
![]() корисності
корисності
![]() -го
товару, еластичність
-го
товару, еластичність
![]() корисності
-го
товару (або коефіцієнт еластичності),
загальна еластичність корисності
корисності
-го
товару (або коефіцієнт еластичності),
загальна еластичність корисності
![]() ,
гранична норма
,
гранична норма
![]() заміщення
заміщення
![]() -го
товару
-тим
товаром та еластичність
-го
товару
-тим
товаром та еластичність
![]() такого заміщення. Формули для обчислення
цих характеристик такі:
такого заміщення. Формули для обчислення
цих характеристик такі:
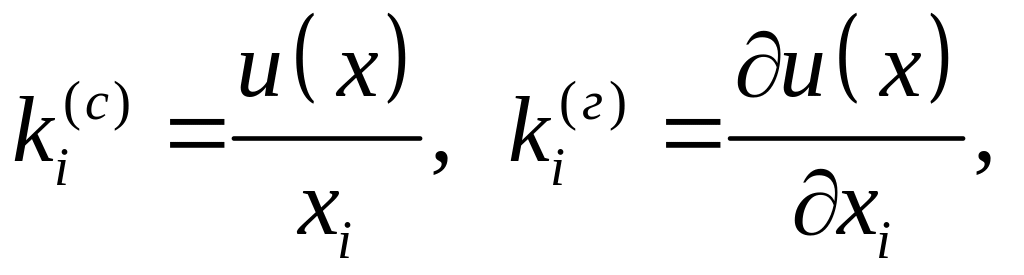 (1.2)
(1.2)
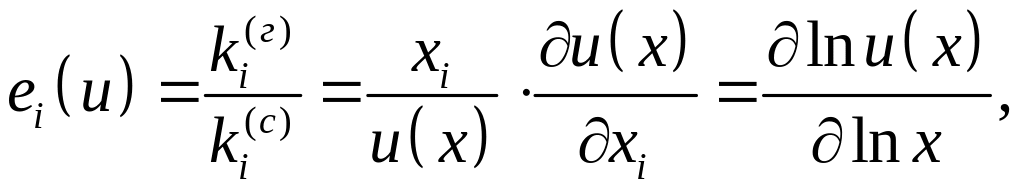 (1.3)
(1.3)
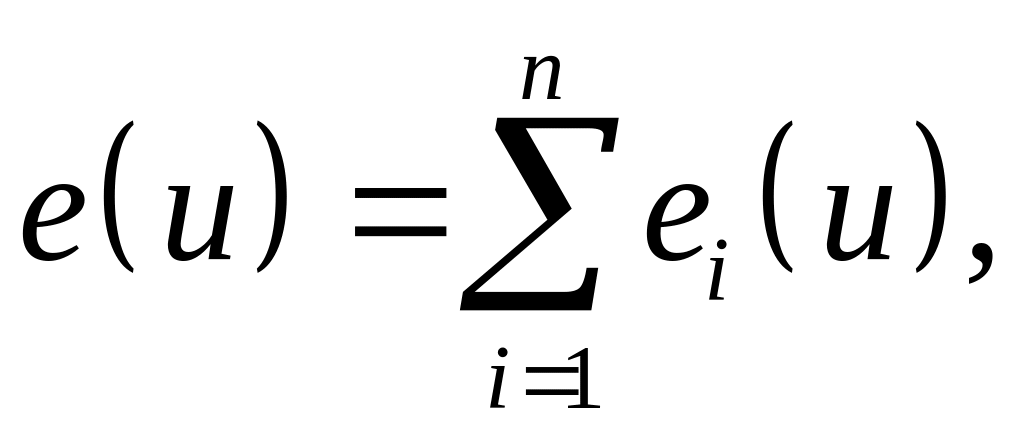 (1.4)
(1.4)
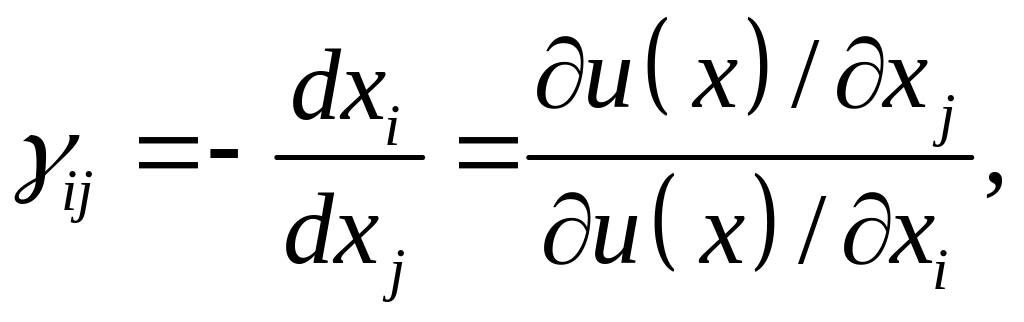 (1.5)
(1.5)
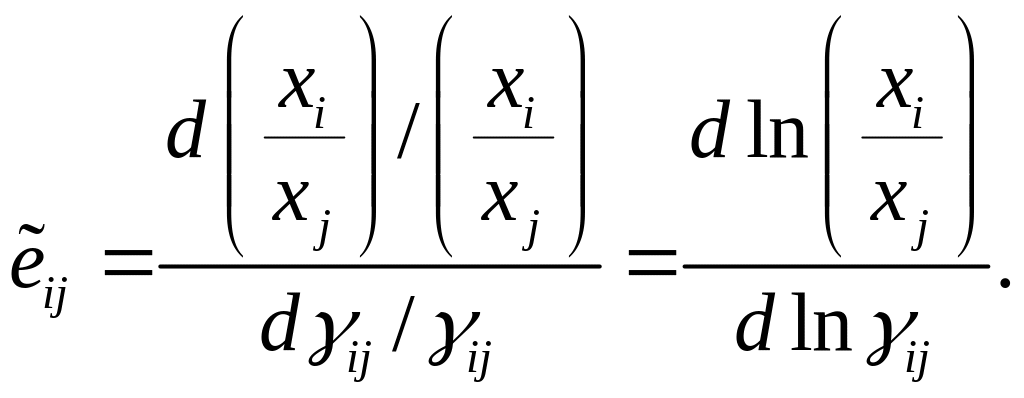 (1.6)
(1.6)
Зрозуміло, що числові значення характеристик (1.2)-(1.6) одержуються при фіксованих значеннях товарів.
Економічна інтерпретація характеристик така:
– середня корисність на малу одиницю -го товару;
– граничний приріст корисності на малу одиницю приросту -го товару;
– процентний приріст корисності на 1% приросту -го товару;
– сумарна еластичність корисності;
– кількість одиниць -го товару, яка необхідна для заміщення вибувшої однієї малої одиниці -го товару, щоб корисність не змінилась;
– процентний
приріст відношення
![]() (товарів
та
)
на 1% приросту граничної норми
заміщення
-го
товару
-тим
товаром.
(товарів
та
)
на 1% приросту граничної норми
заміщення
-го
товару
-тим
товаром.
Наведемо найбільш поширені типи функцій корисності, що задовольняють перелічені вище властивості.
