3. Порівняйте між собою пейсмекери та автопейсмекери.

1) В середовищах автоколивного типу ( їх джерела називаються песмейкери) виникають на локальних неоднорідностях де існує підвищенна порівняно з онорідними ділянка частота автоколивань.

2) В літературі існує дві точки зору на механізм виникнення джерел концентричних автохвиль у середовищах із відновленням. Одна з них полягає в тому, що виникнення пейсмекерів пов’язане з локальними неоднорідностями середовища (домішки, бульбашки газу). В околі таких сторонніх включень елементи середовища спонтанно переходять в автоколивний режим. З цієї точки зору автопесмейкери мають туж природу виникнення, що і песмейкери

Інша точка зору полягає в тому, що джерелом концентричних хвиль є пара елементів середовища, які коливаються в протифазі та періодично збуджують один одного. Така ситуація в принципі можлива, якщо час рефрактерності буде меншим від часу перебування в збудженому стані. Джерела такого типу дістали в літературі назву автопейсмекерів.

Якщо слідувати другій точці зору то в результаті нестікості типу згину , або зсуву Автопесмейкери таких середовищах виникають в результаті виникнення поділу фронту, або джерела типу луна!

4. Чи можливі, на Вашу думку, автономні джерела періодичних автохвиль у бістабільних середовищах?

Оскільки в таких середовища існують два стаціонарні стани то система з часом перейде в один із них, а щоб вивести зі стану рівноваги і створити періодичні автохвилі треба прикласти зовнішнє збурення у вигляді зовнішнього джерела періодичних збурень і тому автономних джерел періодичних автохвиль не виникає.

1. Запропонуйте кілька прикладів систем, у яких можлива дифузійна нестійкість.

1)Такими системами є ситсема хижак здобич.

2) Горііння сухого лісу за наявності пожежників: . Нехай деяка область заросла сухим лісом, у якому легко виникають вогнища пожеж. За безпекою слідкують пожежники, озброєні відповідною технікою, включаючи швидкісні гелікоптери. Коли виникає чергове вогнище пожежі, пожежників поруч мало, тому вогонь деякий час поширюється. Але потім прилітає велика кількість пожежників на гелікоптерах, які локалізують вогонь, зосереджуючись над областю горіння. В результаті утвориться плямиста структура – області вцілілого лісу чергуватимуться зі згарищами.

3) Якщо виходти з моделі морфогенезу Тьюрігна то прикладо такої системи є розподіл в початково однорідній сситемі морфогенів ( плямистітсь у тварин).

2. Чи будуть властивості структур, що виникають у двовимірній області внаслідок розвитку дифузійної нестійкості, залежати від форми цієї області?

Очевидно, що буде якщо враховувати наявність дифузії оскільки формою області буде визначатись дифузійний доданок, а також звильове число k – можливі дискретні значення ( вже по двум координатам) якого буде залежати від форми середовища.

2.4.2

1. Які рівняння використовують для аналізу конвекції Релея – Бенара?

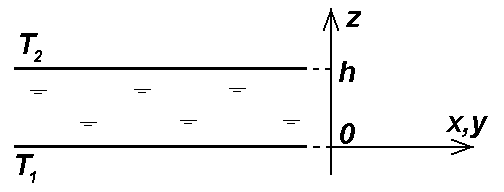
Розглянемо шар в’язкої рідини, що займає проміжок 0<z<h (вісь z спрямовано вертикально вгору, див. рис. 2.2.4). У площині z=0 підтримується температура Т₁, в площині z=h –температура Т₂ (ТТ₁–Т₂>0).

Рис. 2.2.4. Шар рідини, що підігрівається знизу

При невеликих значеннях різниці температур Т рідина залишається нерухомою, так що передача тепла знизу вгору відбувається лише за рахунок теплопровідності. При переході Т через деяке критичне значення Т_cr починається конвекція.

Будемо характеризувати рідину полем температур T(r,t) та полем швидкостей v(r,t). Для її опису скористаємося рівнянням Нав’є – Стокса, а також рівняннями теплопровідності та неперервності.

Рівняння Нав’є – Стокса являє собою, по суті, другий закон Ньютона для краплі рідини з урахуванням того, що положення краплі з часом змінюється. Тому повна похідна dv/dt набуває вигляду

. (2.2.6)

Рівняння Нав’є – Стокса можна записати у вигляді

, (2.2.7)

де  – густина рідини, р – її тиск,  – її коефіцієнт внутрішнього тертя (динамічна в’язкість), g=–ge_z – прискорення земного тяжіння. Доданки в правій частині визначають сили, що діють на краплю рідини. Перший з них відповідає тиску, другий та третій – тертю, четвертий – силі тяжіння.

Рівняння теплопровідності з урахуванням можливої конвекції рідини набуває вигляду

, (2.2.8)

де  – коефіцієнт температуропроводності, а символ  позначає лапласіан.

Нарешті, рівняння неперервності для рідини має вигляд

. (2.2.9)