2. Опишіть часову еволюцію фазових хвиль в автоколивному середовищі, яке має два локальні максимуми для частоти локальних автоколивань.

У цьому випадку на цих локальних максимумах, що є неоднорідностями для цього середовища буде підвищена частота автоколивань, а отже виникне два пейсмейкера.

В результаті конкуренції між ними врешті-решт переможе той, якому відповідають найкоротші хвилі , тобто більша частота автоколивань (найглибша яма).

3. Як, на Вашу думку, зміняться властивості пейсмекера, якщо збурення в середовищі, яке його породило, не буде аксіально-симетричним?

За відсутності аксіальної симетрії маємо двовимірну задачу, тобто в 2.3.24а . (2.3.24 а)

буде залежність не тільки від радіальної компоненти, а й азимутальної. Пошук розв’язку цього рівняння у аналогії з хвильовим призведе до ускладнення симетрії хвиль, що генеруватимуться, а саме, виникнуть періодичні розв’язки за азимутальним кутом як в атомних орбіталях (гантелі в p, d, f…).

4. Як властивості локального збурення впливають на характеристики відповідного пейсмекера?

(2.1.98 а)

Розв’язок (2.1.98 а) описує концентричні фазові хвилі з частотою

(2.1.101)

і хвильовим числом

, (2.1.102)

що розходяться від центру. Чим глибша яма, тим більша λ₁ і, як випливає з (2.1.101)-(2.1.102), тим вища частота і менша довжина хвилі.

Навпаки, при r>R(t) φ≈const, тобто ця область залишається незбуреною (в ній існують синфазні автоколивання з частотою ω_∞).

Область, зайнята фазовими хвилями, розширюється з радіальною швидкістю

. (2.1.103)

Якщо в потенціальній ямі, що відповідає збуренню ω₀(r), існує кілька зв’язаних станів, картина істотно не зміниться. Треба лише замінити λ₁ на максимальне власне число λ_n.

В одно- і двовимірному випадку будь-яка яма (навіть дуже неглибока) містить хоча б один зв’язаний стан. Отже, як завгодно мале додатне збурення ω породжує пейсмекер. У тривимірному випадку зв’язаний стан з’являється лише для достатньо глибоких потенціальних ям, тобто за виконання умови

(2.3.32)

(чим більший радіус ями r₀, тим менша „критична глибина” δω_кр, необхідна для виникнення пейсмекера). При невиконанні умови (2.3.32) пейсмекер не виникає.

Виконаний розрахунок справедливий лише тоді, коли радіус локалізації r_n (2.3.25) задовольняє умові (2.3.20), тобто при λ_n<<1/_, інакше рівняння для λ–ω моделі не зводиться до рівняння для фазових хвиль. Оскільки завжди

, (2.3.33)

(максимальне власне значення λ_n обмежене глибиною потенціальної ями), отримаємо:

, (2.3.34)

тобто виконаний розрахунок справедливий лише для помірних збурень автоколивного середовища.

2.3.5

1. Порівняйте між собою джерела автохвиль типу поділу фронту та типу “луна”

1) Поділ фронту реалізуєиться з нерухомим фронтом при n₂>n_cr>n₁ за рахунок нестійкості при збуренні типу вигину, а луна реалізуються з нерухомим фронтом при n₂>n_cr>n₁ за рахунок нестійкості при збуренні типу зсуву, а швидкість накопичення та розпаду інгібітору по різні боки від нерухомого фронту різні.

2)На відміну від поділу фронту в луні: тривалість імпульсів тепер буде меншою, ніж проміжок між сусідніми імпульсами

3) На відміну від поділу фронту в луні: хвилі перекидання в різні боки від нерухомого фронту будуть відбігати неодночасно.

2. Чим визначається тривалість біжучих імпульсів, генерованих джерелом типу “луна”?

Тривалість імпульсів визначається різницею між швидкостями накопичення та розпаду інгібітору по різні боки від нерухомого фронту

3. Чи може тривалість імпульсів горіння, генерованих джерелом типу “луна”, перевищувати проміжок між ними? Якщо може, то за яких умов?

Може якщо швидкість розпаду інгібітору буде більше ніж накопичення.

4. Чи можна в двовимірній моделі створити автопейсмекер на основі джерела автохвиль типу «поділ фронту»?

Зробити це можна але така динамічна дисипативна структура у двовимірній моделлі буде нестійкою. Стійкою вона має бути лише в тривимірній моделі.

5. Чи можна в двовимірній моделі створити автопейсмекер на основі джерела автохвиль типу “луна”?

Зробити це можна але така динамічна дисипативна структура у двовимірній моделлі буде нестійкою. Стійкою вона має бути лише в тривимірній моделі.

6. Намалюйте епюри зміни температури та концентрації інгібітору по обидва боки від джерела типу «поділ фронту» з урахуванням взаємної залежності температури стаціонарного стану та концентрації інгібітору.

Н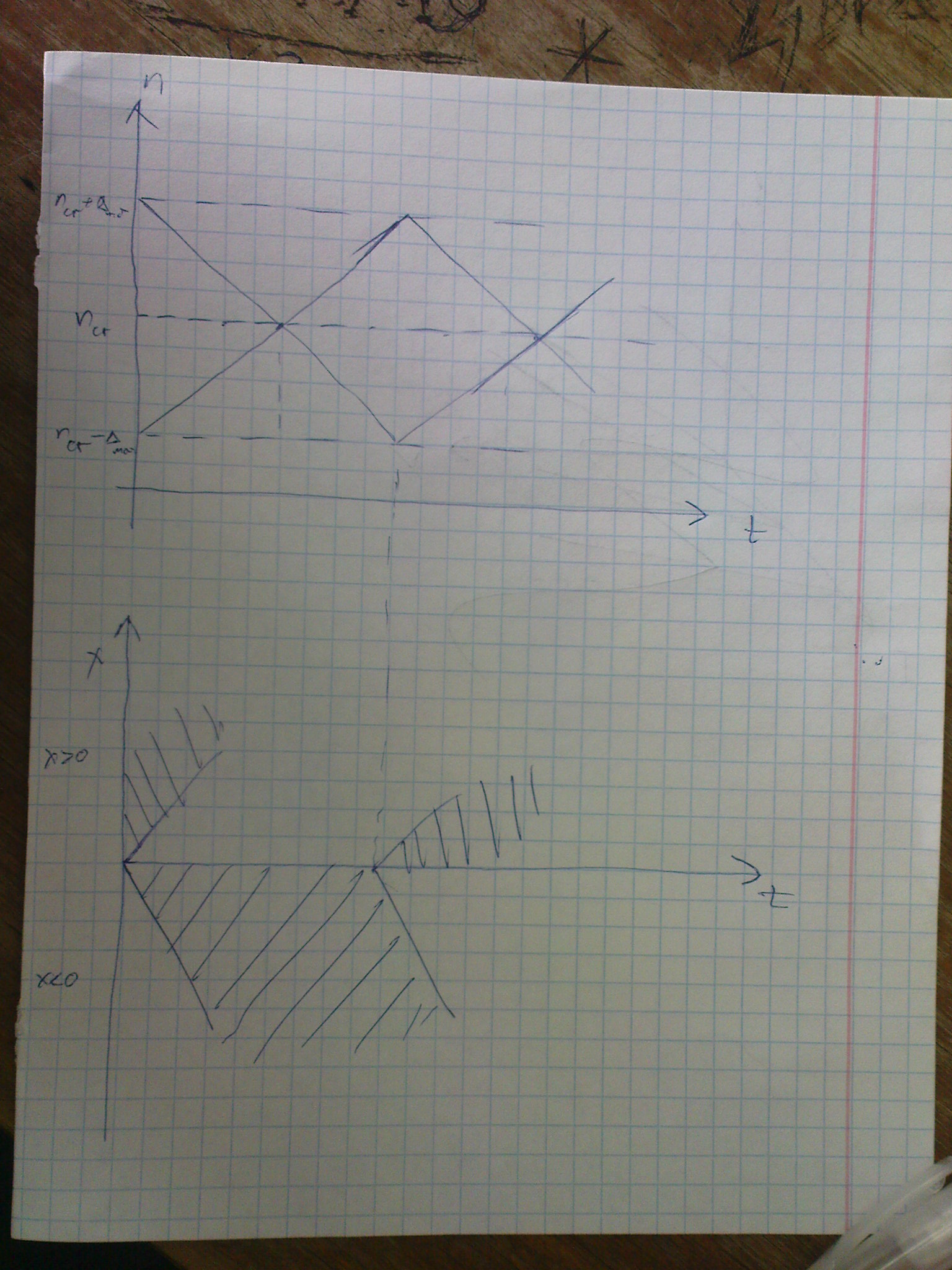 ехай у початковий момент часу в точці х=0 існує стійкий нерухомий фронт збудження (рис. 2.3.14 а). Це означає, що в області х<0 горіння відсутнє, і там n₁>n_cr. В області х>0, навпаки, відбувається горіння, і n₂<n_cr. З часом в області х<0 з концентрація інгібітору зменшуватиметься (нагадаємо, що за відсутності горіння інгібітор розпадається), а в області х>0 – навпаки, збільшується (горіння приводить до виділення інгібітору) – рис. 2.3.15 а. Через певний час концентрації в областях х>0 та х<0 вирівнюються, так що n₁=n₂=n_cr. Після цього різниця n₂–n₁ стає додатною і в деякий наступний момент часу зростає настільки, що реалізується граничний випадок (рис. 2.3.12 б), який, як відзначалося вище, є нестійким щодо малих збурень. Очевидно, це відбудеться при n_2,1=n_cr_max. В результаті зростання збурень типу вигину почне розвиватися нестійкість, і від колишнього нерухомого фронту побіжать дві хвилі перекидання – хвиля запалювання в область х<0 та хвиля гасіння в область х>0 (рис. 2.3.15 б). На місці ж стрибка концентрації інгібітору знову виникне стрибок температури, але знак його зміниться на протилежний. Можна вважати, що за час розвитку нестійкості розподіл концентрації інгібітору змінитися не встигає.

На наступній стадії процесу (ділянка повільного руху) концентрація інгібітору в області х<0, де тепер відбувається горіння, поступово зростає, а в області х>0, де горіння відсутнє – зменшується (рис. 2.3.15 а). В якийсь момент одночасно по обидва боки нерухомого фронту названа концентрація проходить через критичне значення. В наступні моменти часу в системі реалізується ситуація n₂<n_cr<n₁, в результаті чого фронт горіння стає нестійким. Подальше зростання різниці n₁–n₂ триває доти, доки не реалізується граничний випадок. При його досягненні знову розвивається нестійкість, в область х>0 біжить хвиля запалювання, в область х<0 – хвиля гасіння, а стрибок температури в точці х=0 змінює знак (рис. 2.3.15 б). Таким чином, у системі відтворюються початкові умови, з яких ми почали розгляд.