Министерство культуры российской федерации

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

Санкт-Петербургский государственный университет кино и телевидения

Кафедра видеотехники

Цифровая обработка аудиовизуальных сигналов

Лабораторная работа №1:

«АНАЛОГОВО-ЦИФРОВОЕ ПРЕОБРАЗОВАНИЕ»

Выполнил: студент 913 группы

4 Курса фтКиТ

Карнаухова Д.С.

Санкт-Петербург

2012

Цель работы:

• Освоение навыков моделирования, обработки и анализа сигналов в среде MatLab.

• Изучение этапов преобразования сигнала в цифровую форму.

Контрольные вопросы

1.Какие этапы включает в себя процесс аналогово-цифрового преобразования?

Преобразование сигнала в цифровую форму состоит из трех этапов:

1) Дискретизация - процесс замены непрерывного во времени сигнала Uа(t) его отсчетами, отстоящими друг от друга на отрезок времени, называемый периодом дискретизации Td.

2) Квантование - процесс замены непрерывного по амплитуде дискретного сигнала Ud[n] на номер уровня квантования по определенному закону. Расстояние между уровнями квантования Δ - называется шагом квантования.

3) Кодирование - процесс преобразования номера уровня квантования в код, по заданному алгоритму.

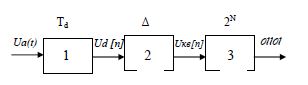
2.Как выбирается частота дискретизации?

Согласно теореме Котельникова непрерывный сигнал с ограниченным спектром частот может быть полностью восстановлен, если передавать отсчеты сигнала с частотой следования (частотой дискретизации Fд), не менее чем в два раза превышающей верхнюю частоту спектра сигнала Fв. Fд > 2Fв.

3. К каким искажениям приводит неправильный выбор частоты дискретизации?

Это приводит к перекрыванию, наложению частотных составляющих спектра, что в свою очередь означает наличие невосстанавливаемых потерь.

4.Как выбирается шаг квантования?

Расстояние между уровнями квантования Δ - называется шагом квантования:

,

где DD-это динамический диапазон сигнала,

N – выбранное количество уровней квантования .

По принципу «чем меньше-тем лучше», потому что так будет точнее передаваться форма сигнала, таким образом шаг квантования должен быть много меньше диапазона вариации входного сигнала.

5. К каким искажениям приводит неправильный выбор шага квантования?

При квантовании мы теряем маленькие (меньше) изменения сигнала. Кроме того, ,получившийся после квантования сигнал отличается от реального (но уже дискретизированного) сигнала на величину порядка шага квантования (или кванта) . Это различие носит название шума квантования, и оно принципиально неустранимо.

6.Как нужно изменить алгоритм квантования, чтобы квантованные значения сигнала не имели знака?

Можно добавить постоянную составляющую, чтобы весь сигнал располагался выше нуля.

7. Какие виды кодирования вы знаете?

1.Бинарное кодирование

1.1. Без возврата к нулю

Потенциальное кодирование, также называется кодированием без возвращения к нулю (NRZ). При передаче последовательности единиц сигнал, в отличие от других методов кодирования, не возвращается к нулю в течение тракта.

Достоинства метода NRZ:

-Простота реализации.

-Метод обладает хорошей распознаваемостью ошибок (благодаря наличию двух резко отличающихся потенциалов).

-Основная гармоника имеет достаточно низкую частоту (равную N/2 Гц, где N- битовая скорость передачи дискретных данных [бит/с]), что приводит к узкому спектру.

Недостатки метода NRZ:

-Метод не обладает свойством самосинхронизации. Даже при наличии высокочастотного тактового генератора, приемник может ошибиться с выбором момента съема данных, так что частоты двух генераторов никогда не бывают полностью идентичны. Поэтому при высоких скоростях обмена данными и длинных последовательностях единиц или нулей небольшое рассогласование тактовых частот может привести к ошибке в целый такт и, соответственно, считыванию некорректного значения бита.

-Вторым серьезным недостатком метода, является наличие низкочастотной составляющей, которая приближается к постоянному сигналу при передаче длинных последовательностей нулей и единиц. Из-за этого многие линии связи, не обеспечивающие прямого гальванического соединения между приемником и источником, этот вид кодирования не поддерживают. Поэтому в сетях код NRZ в основном используется в виде различных его модификаций, в которых устранены как плохая синхронизация кода, так и проблемы постоянной составляющей.

1.2. С возвратом к нулю

То есть каждый бит передается 3-мя уровнями напряжения. Поэтому требуется в 2 раза большая скорость по сравнению с обычной скоростью. Используется в оптоволокне. Это биполярный код, то есть изменение сигнала происходит между 3-мя уровнями.

2. Манчестерское кодирование

При манчестерском кодировании каждый такт делится на две части. Информация кодируется перепадами потенциала в середине каждого тракта. Единица кодируется перепадом от низкого уровня сигнала к высокому, а нуль- обратным перепадом. В начале каждого тракта может происходит служебный перепад сигнала, если нужно представить несколько единиц или нулей подряд. Так как сигнал изменяется по крайне мере один раз за такт передачи одного бита данных, то манчестерский код обладает хорошими самосинхронизирующими свойствами. У манчестерского кода нет постоянной составляющей (меняется каждый такт), а основная гармоника в худшем случае (при передаче последовательности единиц или нулей) имеет частоту N Гц, а в лучшем случае(при передаче чередующихся единиц и нулей)- N/2, как и у NRZ. В среднем ширина спектра при манчестерском кодировании в два раза шире, чем при NRZ кодировании.

3. Дифференциальное манчестерское кодирование

3.1. AM1

AM1- код использует следующие представления битов:

Биты 0 представляются нулевым напряжением (0 В);

Биты 1 представляются поочередно значениями –U или +U (В).

AM1-код обладает хорошими синхронизирующими свойствами при передаче серий единиц и нулей и сравнительно прост в реализации. Недостатком кода является ограничение на плотность нулей в потоке данных, поскольку длинные последовательности нулей ведут к потере синхронизации.

3.2. HDB3

Код HDB3 исправляет любые 4 подряд идущие нули в исходные последовательности. Правило формирования кода следующее: каждые 4 нуля заменяются 4 символами, в которых имеется хотя бы один сигнал V. Для подавления постоянной составляющей полярность сигнала V чередуется при последовательных заменах. Для замены используются два способа: если перед заменой исходный код содержал нечетное число единиц, то используется последовательность 000V, если четное то 100V, где V- сигнал единицы запрещенного для данного сигнала полярности .

3.3. MLT-3

MLT-3 Multi Level Transmission-3(многоуровневая передача)- метод кодирования, использующий три уровня сигнала. Метод основывается на циклическом переключении уровней -U ,0, +U, 0. Единице соответствует переход с одного уровня сигнала на следующий. Так же как и в методе NRZ при передаче нуля сигнал не меняется. В случае наиболее частого переключения уровней (длинная последовательность единиц) для завершения цикла необходимо четыре перехода. Это позволяет вчетверо снизить частоту несущей относительно тактовой частоты, что делает MLT-3 удобным методом при использовании в качестве среды передачи медных проводов. Метод разработан Cisco Systems для использования в сетях FDD1 на основе медных проводов, известных как CDD1. Также используется в Fast Ethernet 100ASE-TX.

Рабочее задание:

1. Рассчитать и построить аналоговый Ua и дискретный Ud сигналы с заданными параметрами Т – период, А – амплитуда, при заданном периоде дискретизации Td. Полученные графики перенести в отчет, отметить временные и амплитудные значения.

Вариант 11:

1.Построить дискретный сигнал на базе косинусоидального аналовогово сигнала с периодом T=300 мс и амлитудой A=15 В, без постоянной составляющей, период дискретизации Td выбрать 15 мс.

Текст программы:

T=0.3;

A=15;

Td=0.015;

t=[0:Td:T];

figure

stem(t,15*cos(2*pi/T*t));

figure

t1=[0:0.05:T];

stem(t1,15*cos(2*pi/T*t1));

figure

t2=[0:0.005:T];

stem(t2,15*cos(2*pi/T*t2));

2. Повторить расчеты для двух других случаев, когда период дискретизации больше и меньше заданного в примере. Полученные графики перенести в отчет, отметить временные и амплитудные значения, сравнить полученные результаты.

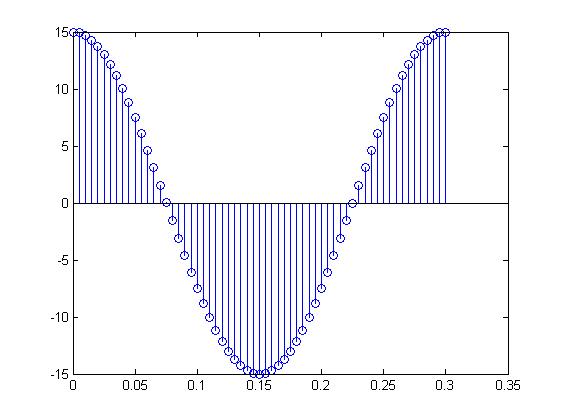
3. Рассчитать квантованный сигнал Uкв на базе дискретного сигнала Ud при заданном количестве уровней квантования – N, используя четыре метода округления round, ceil, floor и fix. Построить квантованные сигналы на одном графике и сравнить результаты.

Вариант 11:

Рассчитать и построить квантованный сигнал выбрав количество уровней квантования 16.

N=16;

delta=30/(N-1);

for k=1:T/Td+1

Ukv1(k)= round(15*cos(2*pi/T*t(k)));

Ukv2(k)= ceil(15*cos(2*pi/T*t(k)));

Ukv3(k)= fix(15*cos(2*pi/T*t(k)));

Ukv4(k)= floor(15*cos(2*pi/T*t(k)));

end

stairs(t,Ukv1,'g');

hold on

stairs(t,Ukv2,'r');

stairs(t,Ukv3,'b');

stairs(t,Ukv4,'y');

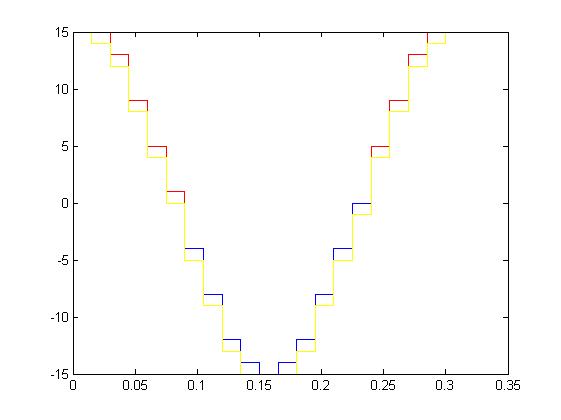
4. Рассчитать ошибку квантования Err=Ud - Uкв и построить гистограммы распределения ошибок квантования для каждого метода. Полученные графики перенести в отчет, отметить временные и амплитудные значения. Сравнить полученные результаты.

Текст программы:

Ud=15*cos(2*pi/T*t);

[H1,X1]=hist(Ud-Ukv1,[-1:0.005:1]);

figure

grid on

subplot(2,2,1)

bar(X1,H1);

[H2,X2]=hist(Ud-Ukv2,[-1:0.005:1]);

subplot(2,2,2)

bar(X2,H2);

[H3,X3]=hist(Ud-Ukv3,[-1:0.005:1]);

subplot(2,2,3)

bar(X3,H3);

[H4,X4]=hist(Ud-Ukv4,[-1:0.005:1]);

subplot(2,2,4)

bar(X4,H4);

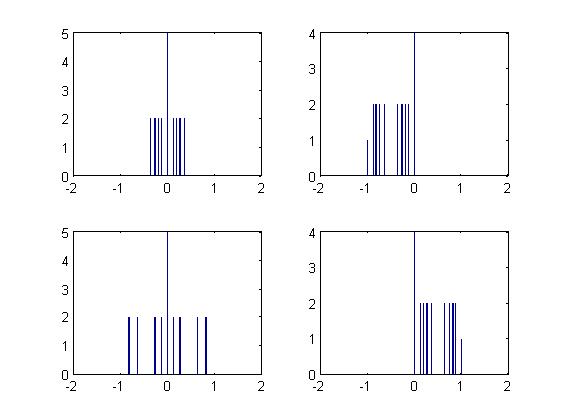
5.Проанализировать диаграммы распределения ошибок квантования: рассчитать среднее значение ошибки, максимальное и минимальное отклонения и среднеквадратичное отклонение, используя функции mean(Err) и std(Err), для каждого метода. Сравнить результаты и сделать выводы.

Текст программы:

err1=mean(Ud-Ukv1)

sko1=std(Ud-Ukv1)

err2=mean(Ud-Ukv2)

sko2=std(Ud-Ukv2)

err3=mean(Ud-Ukv3)

sko3=std(Ud-Ukv3)

err4=mean(Ud-Ukv4)

sko4=std(Ud-Ukv4)

err1 =

-4.2823e-016

sko1 =

0.2261

err2 =

-0.4286

sko2 =

0.3442

err3 =

-4.2294e-016

sko3 =

0.4816

err4 =

0.4286

sko4 =

0.3442