Решение системы уравнений методом прогонки
Метод прогонки, так же как и метод Гаусса, разделяется на два этапа: прямой и обратный ход. В результате прямого хода вычисляются вспомогательные переменные, называемые прогоночными коэффициентами. На обратном ходе получают значения неизвестных.
Метод прогонки специально создан для решения систем линейных алгебраических уравнений с трехдиагональной матрицей, т.е. для систем вида (5).
Рис. 1
Системы такого вида часто возникают при решении различных задач вычислительной математики (например, при численном решении дифференциальных уравнений и интерполировании сплайнами)
Для решения системы уравнений выразим x1 из первого уравнения системы (5):
(6)
Выражение для x1 подставим во второе уравнение системы (5):
Выражая из последнего соотношения x2, получаем:
.
(7)
Выражение для x2 подставим в третье уравнение системы (5) и так далее. На i-м шаге описанного процесса (1 < i < n) i-е уравнение системы приводится к такому же виду:
, где
(8)
, 
На
последнем n-м
шаге подстановки получаем n-е
уравнение в виде 
.
Отсюда можно выразить неизвестное
xn:
(9)
Значения остальных неизвестных вычисляются в процессе обратного хода по формулам (8).
Таким
образом, прямой ход состоит в вычислении
прогоночных коэффициентов 
и 
по
формулам:
,
, 
, (10)
, 
, 
(11)
Обратный ход метода прогонки дает значения неизвестных по формулам:
, 
. (12)
Отметим, что метод прогонки относится к классу экономичных методов. Экономичными называются методы, для которых число требуемых арифметических операций пропорционально числу неизвестных. Для реализации вычислений по описанному алгоритму требуется примерно 8n арифметических операций (тогда как в методе исключения Гаусса эта величина примерно 2 n3/3). Экономичность в данном случае достигается за счет того, что при реализации метода не выполнялись операции над нулевыми элементами исходной матрицы.
Пример использования метода прогонки (алгоритма Томаса) для решения у трёхдиагональной системы линейных уравнений представлен на рис. 2. Пользователь задаёт матрицу коэффициентов уравнений и столбец ответов. Результат сравнивается с ответом встроенного средства решения линейных уравнений программы (метод обратной матрицы).
Трехдиагональной
матрицей называют матрицу вида
.
Задание. При выполнении лабораторной работы необходимо изучить программную реализацию метода прогонки (рис. 2), ввести программу в компьютер и решить примеры в соответствии со своим вариантом.
Решение системы уравнений методом итерации
Наиболее распространенным приемом аналитического решения систем линейных уравнений является алгоритм последовательного исключения неизвестных. Этот метод носит название метода Гаусса. При большом числе неизвестных линейной системы схема метода Гаусса, дающая точное решение, становится весьма сложной. В этих условиях для нахождения корней системы иногда удобнее пользоваться приближенными численными методами. Изложим здесь один из этих методов — метод итерации.
Пусть дана линейная система (1), запишем ее в виде матричного уравнения
Ах = b.
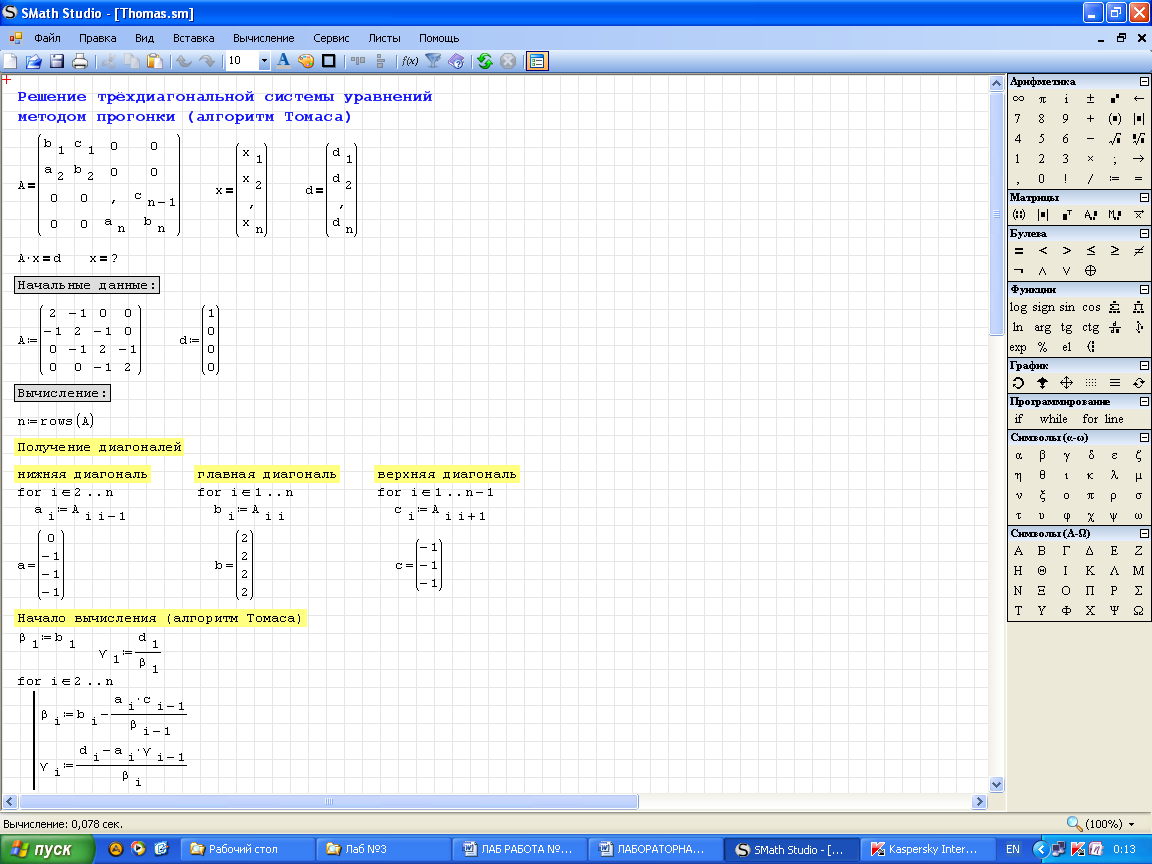
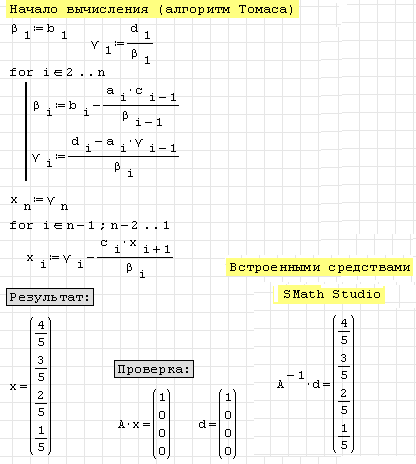
Рис. 2
Предполагая, что диагональные коэффициенты
решим первое уравнение системы (1) относительно x1, второе — относительно х2 и т. д. Тогда получим эквивалентную систему
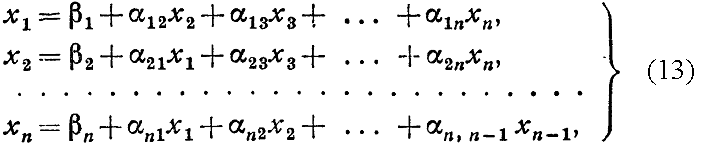
где
и αij=0 при i = j (i,j =1, 2, …, n).
Введя матрицы
систему (5) можно записать в матричной форме
x = β + αx. (14)
Систему (13) будем решать методом последовательных приближений. За нулевое приближение принимаем, например, столбец свободных членов х(0) = β.
Далее последовательно строим матрицы-столбцы
х(1) = β + αх(0)
(первое приближение),
х(2) = β + αх(1)
(второе приближение) и т. д.
Вообще говоря, любое (k+1)-е приближение вычисляют по формуле
х(k+1) = β + αх(k) (k = 0, 1, 2, ...). (15)
Если последовательность приближений х(0), х(1),…, х(k) ,… имеет предел
то этот предел является решением системы (13). В самом деле, переходя к пределу в равенстве (15), будем иметь:
или
х = β + αх ,
т. е. предельный вектор х является решением системы (13), а следовательно, и системы (1).
Напишем формулы приближений в развернутом виде:
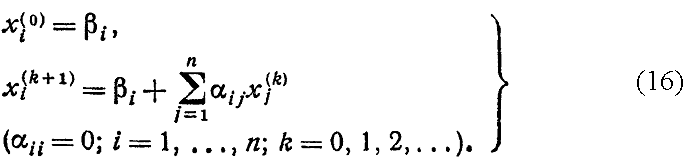
Метод последовательных приближений, определяемых формулой (15) или (16), носит название метода итерации. Процесс итерации (15) хорошо сходится.
Число приближений, необходимых для получения корней системы (1) с заданной точностью, невелико, если элементы матрицы малы по абсолютной величине. Иными словами, для успешного применения процесса итерации модули диагональных коэффициентов системы (1) должны быть велики по сравнению с модулями недиагональных коэффициентов этой системы (свободные члены при этом роли не играют).
Задание. При выполнении лабораторной работы необходимо изучить алгоритм метода итерации, разработать программу для его реализации и решить примеры в соответствии со своим вариантом.