Лекция №6 ММвХТ 6 дек 12

Решение алгебраических уравнений и систем уравнений в sMath Studio (ч.2)

Цель: с помощью средств SMath Studio научиться находить аналитические и численные решения алгебраических уравнений и систем уравнений.

Задание:

1. найти все корни уравнения n-й степени: графически, численно и аналитически;

2. сделать проверку полученного решения;

3. найти численное и графическое решение трансцендентного уравнения;

4. сделать проверку полученного решения;

5. исследовать систему уравнений на разрешимость и решить ее;

6. сделать проверку полученного решения.

Введение

Численное решение систем линейных алгебраических уравнений (СЛАУ) – одна из наиболее часто встречающихся задач в научно-технических исследованиях, математической физике (численное решение дифференциальных и интегральных уравнений), экономике, статистике. Поэтому методам решения линейных алгебраических уравнений в современной вычислительной математике уделяется большое внимание.

Все методы решения СЛАУ делятся на две группы – точные (прямые) и итерационные. Точные методы позволяют получить решение системы линейных уравнений за конечное число арифметических операций (метод Гаусса, метод квадратного корня, правило Крамера и т. д.). Использование итерационных методов дает возможность найти приближенное решение системы с заданной степенью точности (метод простой итерации, метод Зейделя, метод последовательной релаксации).

При решении СЛАУ возникает необходимость выбора того или иного метода, который позволит получить эффективный результат с использованием вычислительной техники. В этой ситуации актуализируется проблема сравнительного анализа прямых и итерационных методов решения СЛАУ.

Критериями сравнения точных и итерационных методов решения СЛАУ с использованием вычислительной техники являются:

• область применения метода;

• временные затраты на решение;

• погрешность результата.

При решении разряженных матриц и матриц большой размерности (при N>1000) целесообразно применять итерационные методы. Использование этих методов приводит к экономии машинного времени и оперативной памяти компьютера. Однако ограничивающим фактором является возможность расходящегося итерационного процесса, который не позволяет достигнуть искомого результата. В этом случае единственно возможным является применение прямых методов. При этом как точным, так и итерационным методам присуща определенная погрешность результата

Решение систем уравнений SMath Studio осуществляется аналитическими, символьными и численными методами.

При решении систем уравнений численными методами должно быть задано некоторое начальное приближение для тех переменных, значение которых необходимо найти. Основываясь на этих начальных данных, SMath Studio будет последовательно уточнять решение до тех пор, пока не подберет наиболее точные значения.

1. Решение линейных алгебраических систем уравнений

1. Решение системы уравнений матричным методом

В некоторых химических задачах требуется решение систем линейных уравнений (СЛУ), например, анализ смесей, расчет равновесий многокомпонентных систем, сглаживание кривых, нелинейный регрессионный анализ.

Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных х₁, х₂, …, х_n:

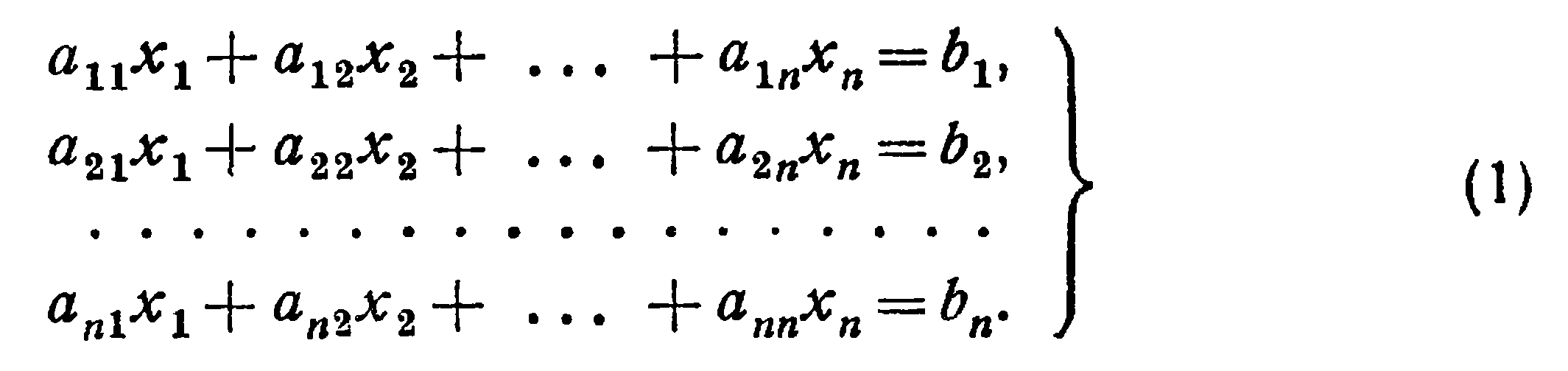
В соответствии с правилом умножения матриц рассмотренная система линейных уравнений может быть записана в матричном виде

Ах = b, (2)

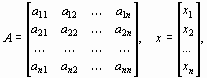
где

.

(3)

Матрица А, столбцами которой являются коэффициенты при соответствующих неизвестных, а строками - коэффициенты при неизвестных в соответствующем уравнении, называется матрицей системы; матрица-столбец b, элементами которой являются правые части уравнений системы, называется матрицей правой части или просто правой частью системы. Матрица-столбец х, элементы которой - искомые неизвестные, называется решением системы.

Если матрица А - неособенная, то есть det A   0, то система (1) или эквивалентное ей матричное уравнение (2) имеют единственное решение. Представленные таким образом системы можно решить как аналитически, так и численно.

Умножая обе части уравнения (2) на обратную матрицу А^-1

A^-1Ax=A^-1b ,

получаем аналитическое решение системы линейных уравнений в матричном виде:

x=A^-1b. (4)

Формула (4) дает решение уравнения (2) и оно единственно. Решение системы линейных уравнений в матричном виде в SMath Studio показано на рис. 1.

Задание. Выполнить решение примера из данного раздела, а также решить уравнения в соответствии с заданным вариантом.