§ 3 Динамический анализ механизмов

Основная задача динамического анализа состоит в определении управляющего силового воздействия - уравновешивающей силы или уравновешивающего момента, приложенного к кривошипу. Эти силовые факторы являются функциями положения кривошипа и в данный момент обеспечивают движение звеньев механизма по заданному закону и уравновешивание механизма.

Дополнительной задачей динамического анализа механизмов является определение реакций в кинематических парах. Знание этих сил необходимо при расчете звеньев механизма на прочность, жесткость, износостойкость, виброустойчивость и других расчетах при проектировании механизмов.

Для проведения динамического исследования применяется метод кинетостатики, основанный на принципе Д^,Аламбера, применительно к механизмам сущность этого метода можно сформулировать так: «Если ко всем внешним, действующим на звено механизма, силам присоединить силы инерции, то под действием всех этих сил звено можно рассматривать условно находящимся в равновесии».

Силовой расчет с применением принципа Д^,Аламбера называется кинетостатическим.

3.1. Определение сил и моментов инерции звеньев

Изучение сил и моментов инерции, действующих на звено механизма, ведут в зависимости от характера движения звена.

Общий случай. Звено АВ совершает плоскопараллель­ное движение (рис. 10). Все точки звена совершают движе­ния с различными по величине и направлению ускорениями. Соответственно этому к каждой материальной точке звена может быть приложена присущая ей элементарная сила инерции:

Как известно из теоретической механики, все эти элемен­тарные силы инерции могут быть сведены к главному вектору сил инерции , приложенному в центре тяжести S звена и к главному моменту сил инерции , которые со­ответственно выражаются формулами:

где т — масса звена, кг; — ускорение центра тяжести, м/с²; — момент инер­ции звена относительно оси, проходя­щей через центр тяжести, кгм²; — угловое ускорение звена, 1/с².

Знаки минус в формулах указывают на то, что главный вектор и главный момент сил инерции направлены в сто­роны, противоположные направлениям соответствующих ускорений.

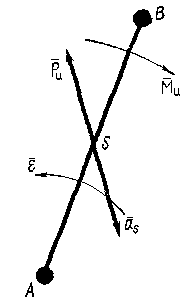
Рис. 10

Частные случаи.

1. Звено совершает вращательное движение вокруг оси, не проходящей через центр тяжести (рис. 11). Здесь аналогично все элементарные силы инерции приводятся к главному вектору сил инер­ции , (H) и к главному моменту сил инерции (Нм). Если звено вращается равномерно ( = 0), то = 0, а ускорение центра масс будет равно нормальной составляющей = , тогда = .

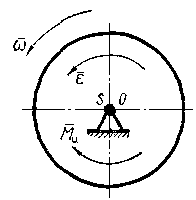
Рис. 11 Рис. 12

2. Звено вращается вокруг оси, проходящей через центр тяжести его (рис 12), например ротор электродвигателя. В этом случае = 0 следовательно главный вектор сил инерции = 0. Если угловое ускорение , то к звену прикладывается только главный момент сил инерции

3. Звено совершает поступательное движение (рис. 13) с ускорением a_s > 0. Считая, что масса звена сосредоточена в центре тяжести S, главный вектор сил инерции выразится так: . Поскольку угловое ускорение ε = 0, то главный мо­мент сил инерции М_и = 0.

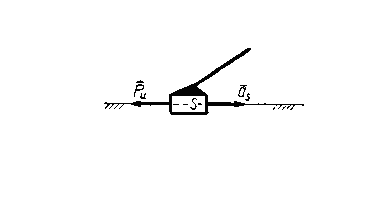
Рис. 13