2.4. Построение планов ускорений

По аналогии с планами скоростей при помощи планов ускорений можно найти ускорения любых точек механизма. При построении планов ускорений также следует пользо­ваться их изображающими свойствами, заключающимися в следующем:

1. Векторы, исходящие из полюса, изображают абсолютные ускорения соответствующих точек механизма в масштабе плана ускорений. Точки плана ускорений, соответствующие точкам, ускорения которых равны нулю, располагаются в полюсе.

2. Векторы, соединяющие концы векторов абсолютных ускорений, выражают в том же масштабе полные относи­тельные ускорения.

3. Полные относительные ускорения на плане ускоре­ний образуют фигуру, подобную одноименной жесткой фи­гуре на плане положения механизма, но повернутую по от­ношению к последней на некоторый угол 180° — в сто­рону мгновенного углового ускорения данного звена, где

Поскольку полные относительные ускорения состоят из геометрической суммы тангенциальных и нормальных составляющих, то обычно концы векторов абсолютных ускорений на планах ускорений обозначают буквами, соответствующими названию точек. Концы векторов нормаль­ных составляющих ускорения обозначают другими буквами, не встречающимися в обозначениях точек механизма.

Пример 5. Методом планов ускорений определить абсо­лютные и относительные ускорения точек звеньев и угло­вые ускорения звеньев для трех положений механизма (рис. 4). Данные взять по условию примера 4.

Решение. Построение плана ускорений рассмотрим на том же положении механизма, что в примере 4.

Определим ускорение точки А. Поскольку звено O₁A вращается равномерно где и , то точка А имеет только нормальное ускорение, которое направлено по звену O₁A к центру вращения. Величина этого ускорения:

м/с .

Принимаем длину отрезка р'а', изображающего вектор ускорения точки А, равной 65 мм. Тогда масштаб плана ускорений

м/с мм.

Из произвольной точки р', принятой за полюс плана ускорений, откладываем параллельно звену О₁А в направ­лении от точки А к точке О₁ отрезок р'а' (рис. 7).

Ускорения точек О₁ и O₂ механизма равны нулю, сле­довательно, точки о'₁ и о₂ будут совпадать с полюсом плана ускорений.

Рассматриваем движение точки В со звеньями АВ и BO₂ и по аналогии с планом скоростей составляем векторные уравнения:

(2.5)

(2.6)

Полные относительные ускорения и , представ­ляем в виде суммы двух составляющих — нормальной, направленной по оси соответствующего звена к центру вра­щения в относительном движении, и тангенциальной, пер­пендикулярной к этому звену. Тогда уравнения (2.5) и (2.6) можно записать в следующем виде:

В этих уравнениях ускорение а_А известно по величине и по направлению, ускорение = 0.

Определяем величины нормальных ускорений:

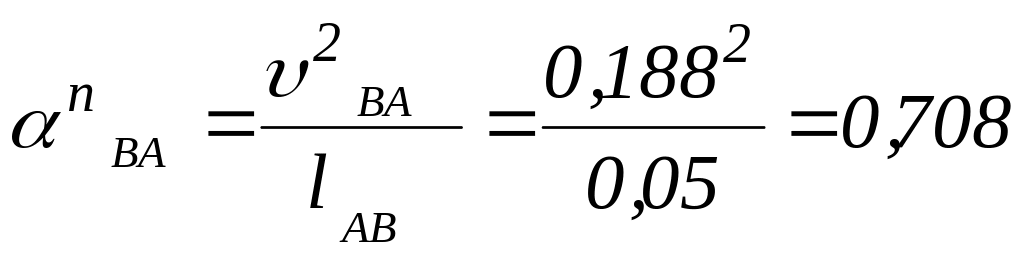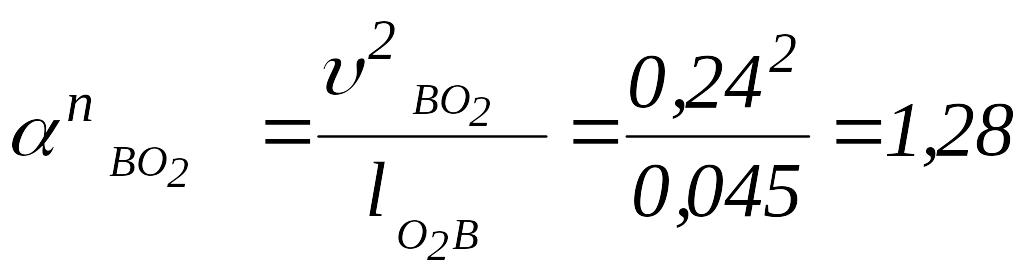м/с ;

м/с .

Ускорение направлено по оси звена АВ от точки В к точке А, ускорение — по оси звена O₂В от точки В к точке O₂.

Относительные тангенциальные ускорения известны только по линиям их действия. Ускорение перпенди­кулярно звену АВ, а ускорение перпендикулярно звену O₂В. Величины и направления тангенциальных ускорений определяем путем построения плана ускорений.

От точки а' плана ускорений параллельно звену АВ в направлении от точки В к точке А откладываем вектор изображающий ускорение . Длина этого отрезка

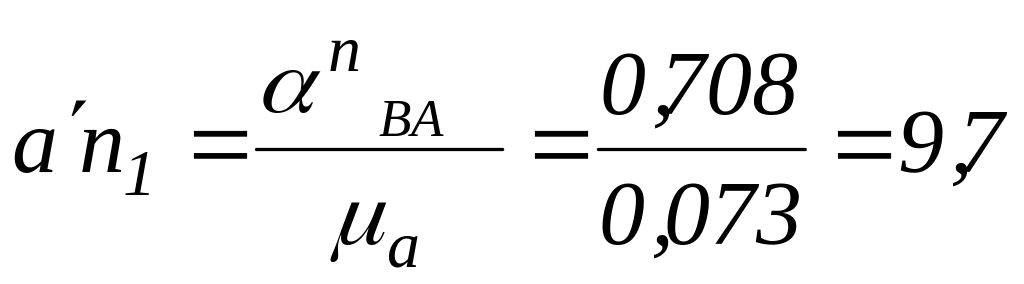мм.

Через точку п₁ проводим перпендикулярно к звену AB линию действия тангенциального ускорения . Затем от точки о'₂ плана ускорений, совпадающей с полюсом р', параллельно звену O₂В в направлении от точки В к точке O₂ откладываем вектор , изображающий ускорение . Определим длину этого отрезка:

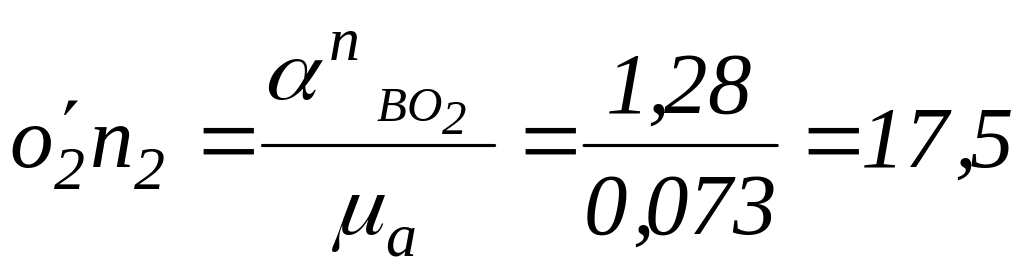мм.

Через точку п₂ проводим перпендикулярно звену O₂В линию действия тангенциального ускорения . На пересечении линий действия ускорений и получим точку b´ — конец вектора р'b', изображающего ускорение точки В механизма:

м/с .

Точка b' определяет также концы векторов и танген­циальных ускорений и :

м/с ;

м/с .

Вектор изображает полное относительное ускорение точки В во вращении вокруг точки А:

м/с .

Вектор полного ускорения точки В во вра­щении относительно точки O₂ механизма совпадает с век­тором абсолютного ускорения точки В. Следова­тельно:

м/с .

Исходя из третьего свойства планов ускорений а'b'с' - относительных ускорений должен быть подобен ABC звена 2, т. е. можно составить пропорции

и .

Поскольку АС =ВС, то

мм.

Из точек а' и b' плана ускорений радиусами, равными соответственно длинам отрезков а'с' и b'с', делаем засечки. Из полученных точек пересечения засекающих дуг (слева и справа от вектора ) в качестве точки с' выбираем точку, расположенную слева, так как при этом порядок букв при обходе треугольника а'b'с' плана ускорений и треуголь­ника ABC механизма будет одинаковым. Соединив полюс плана ускорений с точкой с', получаем вектор абсолютного ускорения точки С механизма:

м/с

Находим положение точки d' на плане ускорений исходя из пропорции

откуда

Следовательно, абсолютное ускорение точки D

м/с .

Для определения ускорения точки Е воспользуемся векторными уравнениями:

(2.7)

(2.8)

где — абсолютное ускорение точки D; — полное относительное ускорение точки Е во вращении вокруг точки D; — ускорение точки Е₀, принадлежащей стойке и совпадающей в данный момент с точкой Е ползуна; — ускорение точки Е в поступательном движении относительно точки E₀. В этих уравнениях:

а) ускорение известно по величине и по направ­лению;

б) полное относительное ускорение представляем состоящим из нормальной и тангенциальной со­ставляющих, тогда уравнение (2.7) принимает вид:

где нормальное ускорение

м/с

направлено по оси звена DE от точки Е к точке D.

Для тангенциального ускорения известна только линия его действия, перпендикулярная к звену DE;

в) ускорение = 0;

г) ускорение известно по линии действия; оно направлено параллельно оси направляющих ползуна.

От точки d' плана ускорений параллельно звену DE в направлении от точки Е к точке D откладываем век­тор , изображающий нормальное ускорение , предварительно определив длину этого отрезка:

мм.

Поскольку его длина в выбранном масштабе плана ускорений не превышает 1 мм, то точки п₃ и d' на плане совпадут (на рис.7 показан общий случай, когда век­тор в масштабе плана имеет достаточную длину).

Из точки п₃ перпендикулярно звену DE проводим линию действия тангенциального ускорения . Поскольку ускорение равно нулю, то точка е'₀ на плане ускоре­ний совпадает с полюсом р'. Через точку е'₀ параллельно оси направляющих ползуна х — х проводим линию дей­ствия ускорения . Точка е' пересечения этих линий действия определяет конец вектора, изображающего абсо­лютное ускорение точки Е:

м/с .

Точка е' определяет также конец вектора , изображающего тангенциальное ускорение . Поскольку в нашем случае точки п₃ и d' на плане совпали, то = - полное относительное ускорение будет равно тангенциальному ускорению :

м/с .

Вектор ускорения совпадает с вектором абсолютного ускорения точки Е. Следовательно,

м/с .

Значения нормальных и тангенциальных ускорений, а также длин отрезков, изображающих их на планах ускорений для трех положений механизма сводим в таблицу 3:

Таблица 3

№ пол

м/с

м/с

м/с

мм

м/с

мм

м/с

мм

м/с

мм

м/с

мм

2

…

…

…

…

…

…

…

…

…

…

…

…

3

0,708

9,7

1,28

17,5

0,011

0,15

4,12

56,5

4,81

66

0,129

3

6

…

…

…

…

…

…

…

…

…

…

…

…

Зная положения центров тяжести S₂, S₃, S₄ на звеньях по аналогии с планом скоростей находим по правилу подобия соответствующие им точки , , на плане ускорений. Соединяем полученные точки с по­люсом плана ускорений и определяем ускорения центров тяжести:

м/с ;

м/с ;

м/с .

Определяем угловые ускорения звеньев. Угловое уско­рение ведущего звена О₁А, совершающего равномерное движение, равно ну­лю.

Угловое ускоре­ние звена 2

1/c .

Для определения направления углово­го ускорения зве­на 2 рассмотрим вра­щение точки В вокруг точки А. Перенесем мысленно вектор тангенциального ус­корения в точку В. В направлении этого вектора точка В вра­щается относительно точки А против часовой стрелки, что и определяет на­правление углового ускорения ₂ (рис. 5).

Угловое ускорение звена О₂B направлено против часовой стрелки (по вращению точки В относительно точки O₂ в направлении вектора тангенциального ускорения ). Величина его определяется по формуле:

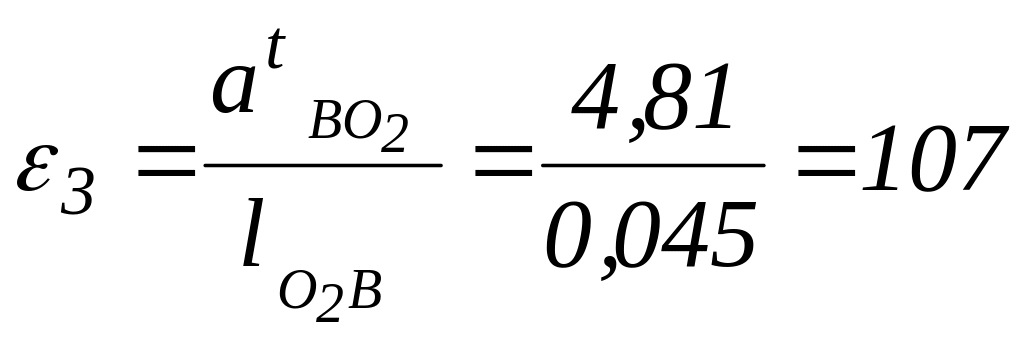1/c .

Угловое ускорение звена DE направлено в соответ­ствии с круговой стрелкой, направленной против часовой стрелки (по вращению точки Е относительно точки D в направлении вектора тангенциального ускорения и определяется по формуле

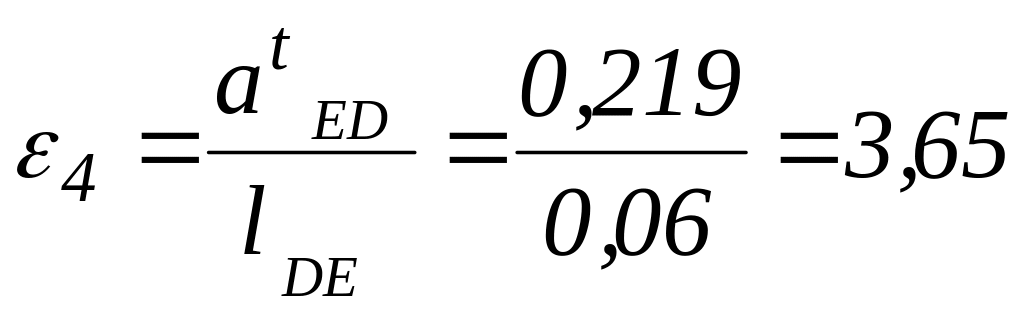1/c .

Звено 5 совершает поступательное движение, поэтому угловое ускорение ; ускорение его центра тяжести , совпадает по величине и направлению с ускорением точки Е.

Полученные значения абсолютных и относительных ускорений точек и значения угловых ускорений звеньев для трех положений механизма сво­дим в таблицу 4.

Таблица 4

№ пол. параметры	2	3	6
, мм	…	65	…
аA, м/с	…	4,75	…
, мм	…	68	…
аB, м/с	…	4,96	…
, мм	…	57,5	…
аBA, м/с	…	4,2	…
, мм	…	72	…
аC, м/с	…	5,25	…
, мм	…	36,4	…
аD, м/с	…	2,66	…
, мм	…	36	…
аE, м/с	…	2,63	…
, мм	…	3	…
аED, м/с	…	0,219	…
, мм	…	60	…
а S , м/с	…	4,38	…
, мм	…	42	…
а S , м/с	…	3,07	…
, мм	…	36	…
а S , м/с	…	2,63	…
ε2, сек-2	…	80,1	…
ε 3, сек-2	…	107	…
ε 4, , сек-2	…	3,65	…