2.2. Построение траекторий точек

Чтобы построить траекторию какой-либо точки, нужно, построить несколько планов положений механизма, найти на каждом из этих планов положение заданной точки и по­следовательно соединить полученные точки плавной кри­вой (рис.4).

Обычно планы положений механизма строятся для не­скольких равноотстоящих положений ведущего звена О₁А. Для этого окружность —- траектория точки А — делится на несколько равных частей. Одно из положений точки А принимается за нулевое, а остальные пронумеровываются в направлении вращения звена О₁А. За нулевое положе­ние точки А кривошипа выбирают такое, при котором даль­нейшее движение точки А в заданную сторону вращения будет соответствовать рабочему ходу исполнительного звена механизма.

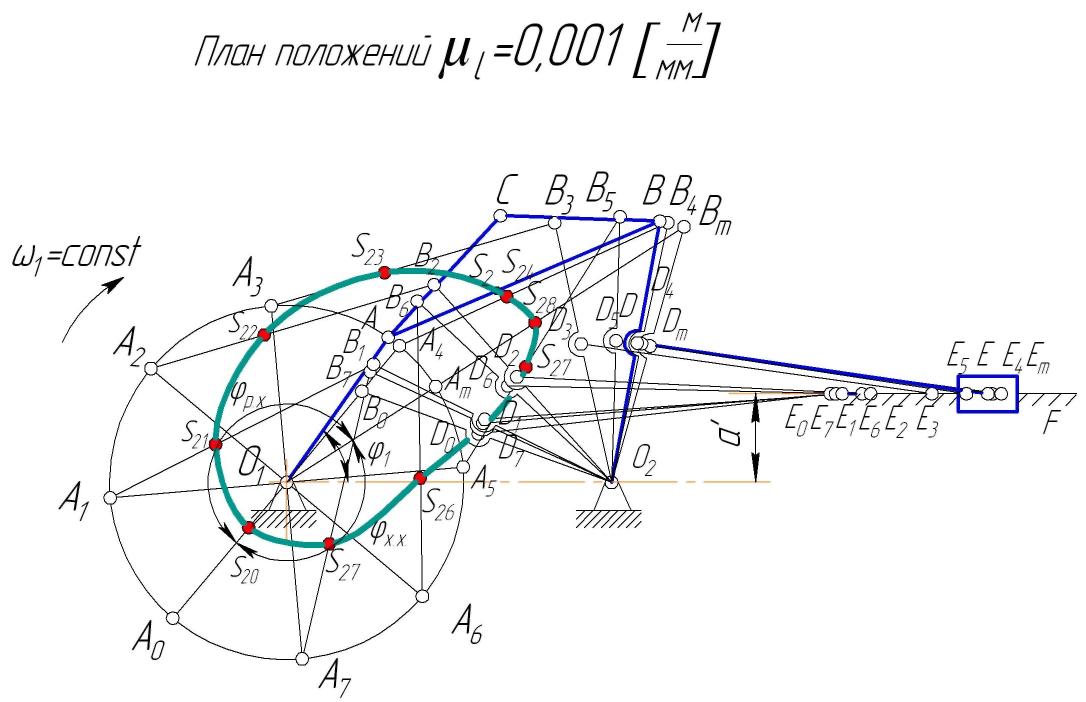
Рис. 4

Пример 3. Для механизма по условию примера 1 построить планы положений по восьми равноотстоящим по­ложениям звена О₁А, начертить траекторию точки S₂ и разместить траекторию точки В, если L_as2 = 0,02 м (рис. 1).

Решение. Кривошип совершает полное круговое движение и траекторией движения точки А будет окруж­ность радиуса О₁А. Проводим эту окружность. Поскольку коромысло 3 совершает качательное движение, то точка В движется по дуге окружности радиуса О₂В. Для разметки траектории точки В необходимо на дуге радиуса О₂В найти крайние положения точки В.

Точка В занимает крайнее левое положение тогда, когда длина О₁А кривошипа вычитается из длины АВ шатуна, и крайнее правое,— когда эти длины складываются.

Для нахождения крайних положений точки В делаем две за­сечки из центра О₁ радиусами r_min= А В — О₁А и r_mах = АВ + О₁А на дуге радиуса O₂B. Получаем точки В₀ и В_т.

На пересечении прямой В₀О₁ с окружностью радиуса О₁А находим точку А₀, а на пересечении прямой В_тО₁ с этой окружностью — точку А_т.

Два крайних положения О₁А₀ и О₁А_т кривошипа делят его полный оборот (угол 360°) на два неравных по величине угла.

Больший из них обычно соответствует рабочему ходу исполнительного звена механизма, меньший — холостому ходу. На рис. 4 эти углы обозначены соответственно φ_рх и φ_хх.

Чтобы при дальнейшем движении в заданную сторону вращения точка А кривошипа двигалась в направлении рабочего хода исполнительного звена механизма, за нуле­вое положение принимаем крайнее левое положение точки А, обозначенное А₀ (рис. 4).

Соединяем точки В₀ и В_т с точкой 0₂, находим поло­жения точек D₀, D_m, E₀, E_m и получаем два положения механизма, соответствующие крайним положениям точки В.

Чтобы упростить дальнейшее построение, положения точки С не наносим.

Разбиваем окружность радиуса О₁А, начиная от точки А₀, на восемь равных частей (в задании на курсовой проект требуется разбить на двенадцать) и нумеруем точки деления в направлении вращения звена О₁А. Используя метод засечек, строим первое, второе и все последующие положе­ния механизма.

Определяем длину отрезка

и находим положения точек S₂₀, S_2l, S₂₂ и т. д.

Соединяем полученные точки плавной кривой. Это и бу­дет траектория точки S₂.

2.3 Построение планов скоростей

Зная закон движения ведущего звена и длины всех зве­ньев механизма, можно определить скорости его точек по величине и направлению в любом положении механизма путем построения плана скоростей для этого положения.

Построение планов скоростей и чтение их во многом упрощаются при использовании свойств этих планов, ко­торые заключаются в следующем:

1. Векторы, исходящие из полюса, изображают абсолют­ные скорости соответствующих точек звеньев механизма в масштабе плана скоростей. Точки плана скоростей, соот­ветствующие неподвижным точкам механизма, находятся в полюсе плана.

2. Векторы, соединяющие концы векторов абсолютных скоростей, выражают величины и направления относитель­ных скоростей.

3. Векторы относительных скоростей точек звена на плане скоростей образуют фигуру, подобную одноимен­ной жесткой фигуре, образованной отрезками, соединяющими эти точки звена на плане механизма, повернутую по отношению к последней на 90° в сторону мгновенного вращения данного звена.

Пример 4. Определить абсолютные и относительные скорости точек звеньев и угловые скорости звеньев в восьми положениях механизма (см. рис. 4) методом планов скоростей. Построить годограф скоростей центра масс S₂ шатуна 2. Кривошип O₁A имеет частоту вращения n₁ = 120 об/мин в направлении по часовой стрелке. Размеры звеньев — те же.

Решение. Построение плана скоростей рассмотрим на примере одного положения механизма, когда угол поворота кривошипа , (это положение на рис. 4 выделено).

Определяем угловую скорость кривошипа О₁А по фор­муле:

1/c.

Из теоретической механики известно, что скорость ка­кой-либо точки звена может быть представлена в виде векторной суммы переносной и отно­сительной скоростей. Тогда абсолютная скорость точки А кривошипа О₁А будет определятся

где - переносная скорость т. О₁ , - относительная скорость т. А во вращении вокруг т. О₁. Т. о., абсолютная скорость совпадает с относительной, поэтому скорость точки А находим по фор­муле

м/с.

Вектор _a направлен перпендикулярно к оси звена O₁A в сторону его вращения.

Задаемся длиной отрезка ра, который будет изображать на плане скорость , точки A; ра = 66 мм. Масштаб плана скоростей

м/с·мм.

От произвольной точки р, принятой за полюс плана ско­ростей, откладываем перпендикулярно к звену О₁А отре­зок ра (рис. 6).

Скорости неподвижных точек О₁ и O₂ равны нулю, поэтому векторы и также равны нулю и, следовательно, токи о₁ и о₂ на плане скоростей совпадают с по­люсом р.

Для определения скорости точки В воспользуемся векторными уравнениями:

(2.1)

(2.2)

где — скорость точки А в переносном движении; — относительная скорость точки В во вращении вокруг точки А; — скорость точки O₂; — относительная скорость точки В во вра­щении вокруг точки O₂.

В этих уравнениях скорость известна по величине и направлению, скорость = 0. Относительные скорости и известны лишь по линии действия: пер­пендикулярна к звену АВ, перпендикулярна к звену 0₂В. Поэтому для определения скорости точки В через точку а (конец вектора скорости ) проводим перпенди­кулярно звену АВ линию действия скорости , а через точку о₂, совпадающую с полюсом р плана скоростей, проводим перпендикулярно звену О₂В линию действия скорости . На пересечении этих двух линий действия получим точку b — конец вектора скорости точки В:

м/с.

Направление скорости определяется направлением вектора .

Согласно уравнению (2.1) вектор изображает относительную скорость точки В во вращении вокруг точки А:

м/с.

Согласно уравнению (2.2) вектор ( ) изображает относительную скорость точки В во вращении вокруг точки O₂:

м/с.

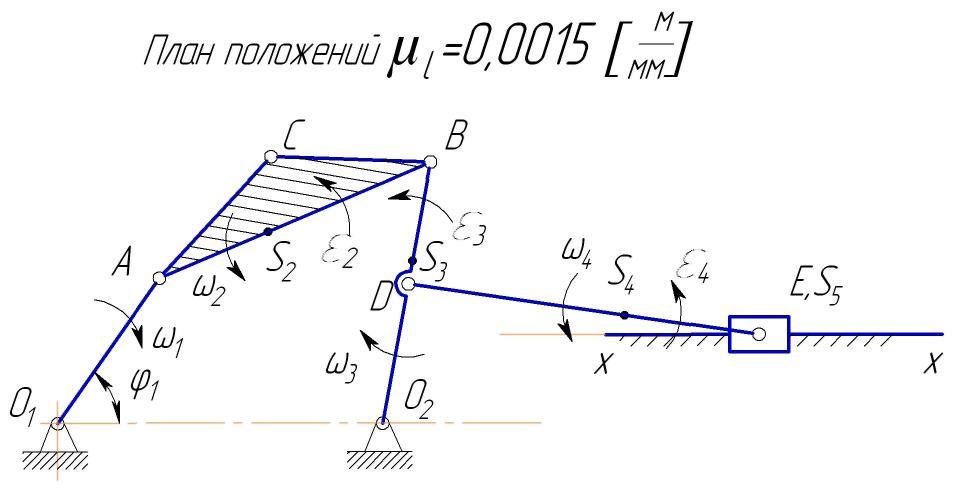
Рис. 5

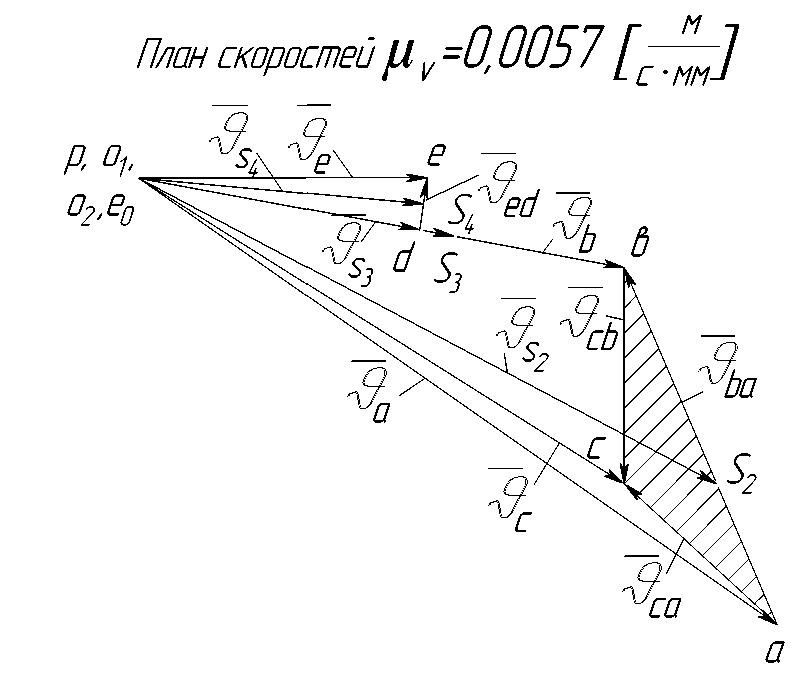
Рис. 6

Рис. 7

Положение точки с (конец вектора скорости точки С) определяем на плане скоростей по теореме подобия (третье свойство планов скоростей). На отрезке ab плана скоростей строим треугольник аbс, подобный треугольнику ABC звена 2. Определяем длины отрезков ас и bc из пропорций

и

Поскольку АС = ВС, то

мм.

Из точек а и b плана скоростей радиусами, равными со­ответственно отрезкам ас и bc, делаем засечки. Получив две точки пересечения этих дуг, справа и слева от вектора . За точку с плана скоростей следует взять ту из полу­ченных точек, при которой порядок букв в треугольниках abc и ABC будет одинаковым. Так, например, при обходе сторон ABC звена 2 по направлению вращения часовой стрелки читаем: А С В. Порядок букв в треуголь­нике abc при обходе сторон треугольника также по часовой стрелке должен сохраниться а с b. Следовательно, точка с плана скоростей будет слева от вектора .

Соединяем полюс плана скоростей р с точкой с и опре­деляем величину скорости точки С:

м/с.

Согласно тому же свойству планов скоростей находим положение точки d на плане исходя из пропорции:

В этом случае фигура относительных скоростей o₂db на плане скоростей будет прямой по подобию с прямой О₂B механизма:

мм.

Определив положение точки d на плане скоростей, нахо­дим величину скорости точки D

м/с.

Скорость точки Е шатуна DE представляем в виде век­торной суммы переносной и относительной скоростей. Для ее определения воспользуемся векторными уравнениями:

(2.3)

(2.4)

где — скорость точки D в переносном движении; — относительная скорость точки Е во вращении вокруг точки D; — скорость точки Е₀, принадлежащей стойке и совпадающей в данный момент с точкой Е ползуна; — скорость точки Е в поступательном движении относительно точки Е₀.

В этих уравнениях скорость известна по величине и направлению, скорость = 0. Относительные скорости и известны лишь по линиям действия: пер­пендикулярна к звену DE, параллельна оси направ­ляющих ползуна. Для определения скорости точки Е через точку d плана скоростей проводим перпендикулярно звену DE линию действия скорости , а через точку е₀, совпадающую с полюсом плана р параллельно оси направляющих ползуна (х — х) — линию действия скорости . Точка е пересечения этих линий действия опреде­ляет конец вектора скорости точки Е. Величина ско­рости

м/с.

Вектор de определяет величину и направление ско­рости

м/с.

Исходя из теоремы подобия (третье свойство планов скоростей) находим на плане точки s₂, s₃, s₄, соответству­ющие центрам тяжести звеньев S₂, S₃ и S_4. Из полюса р в эти точки проводим векторы. Определяем величины скоростей центров тяжести:

м/с;

м/с;

м/с.

Переходим к определению угловых скоростей звеньев. Угловая скорость ω₁ ведущего звена известна по величине и направлению (ω₁ = 12,56 1/с и это звено вращается по часовой стрелке).

Чтобы определить угловую скорость ω₂ звена АВ, рас­смотрим вращение точки В вокруг точки А. Направление скорости точки В во вращении вокруг точки А опреде­ляется направлением вектора . Мысленно переносим этот вектор в точку В механизма и считаем точку А как бы неподвижной. Точка В в направлении вектора враща­ется относительно точки А против часовой стрелки, что и определяет направление вращения звена АВ (рис. 5). Находим величину угловой скорости второго звена по формуле

1/c.

При определении направления угловой скорости ω₃ по­ступаем аналогично. Перенесенный в точку В звена O₂В вектор показывает, что точка В вращается относительно точки O₂ по часовой стрелке. Это определяет направление угловой скорости третьего звена (рис. 5):

1/с.

Чтобы определить угловую скорость ω₄ звена DE, мысленно переносим вектор скорости в точку Е. В направлении вектора точка Е вращается относительно точки D, которую считаем как бы неподвижной, против часовой стрелки, что и определяет направление вращения звена DE. Величина этой угловой скорости

1/с.

Угловая скорость ползуна 5, совершающего прямоли­нейное поступательное движение, равна нулю.

Аналогично строятся планы скоростей для остальных положений механизма.

Полученные значения абсолютных и относительных скоростей точек и значения угловых скоростей звеньев для всех положений механизма сво­дим в таблицу 2.

Таблица 2

	0	1	2	3	4	5	6	7	8
pa, мм	…	…	…	66	…	…	…	…	…
υA, м/с	…	…	…	0,377	…	…	…	…	…
pb, мм	…	…	…	42	…	…	…	…	…
υB, м/с	…	…	…	0,24	…	…	…	…	…
ba, мм	…	…	…	33	…	…	…	…	…
υBA, м/с	…	…	…	0,188	…	…	…	…	…
pc, мм	…	…	…	48	…	…	…	…	…
υC, м/с	…	…	…	0,274	…	…	…	…	…
pd, мм	…	…	…	22,4	…	…	…	…	…
υD, м/с	…	…	…	0,128	…	…	…	…	…
pe, мм	…	…	…	23	…	…	…	…	…
υE, м/с	…	…	…	0,131	…	…	…	…	…
ed, мм	…	…	…	4,5	…	…	…	…	…
υED, м/с	…	…	…	0,0257	…	…	…	…	…
ps2, мм	…	…	…	55	…	…	…	…	…
υ S , м/с	…	…	…	0,314	…	…	…	…	…
ps3, мм	…	…	…	26	…	…	…	…	…
υ S , м/с	…	…	…	0,148	…	…	…	…	…
ps4, мм	…	…	…	22,5	…	…	…	…	…
υ S , м/с	…	…	…	0,128	…	…	…	…	…
ω2, сек-1	…	…	…	3,76	…	…	…	…	…
ω3, сек-1	…	…	…	5,32	…	…	…	…	…
ω4, сек-1	…	…	…	0,428	…	…	…	…	…

Для построения годографа скорости центра масс S₂ шатуна АВ перенесем со всех планов скоростей векторы скорости V_s2 , сохраняя их величину и направление, в общий полюс – произвольно выбранную точку на чертеже (рис. 8). Соединив концы векторов плавной линией, получим годограф скорости т. S₂.

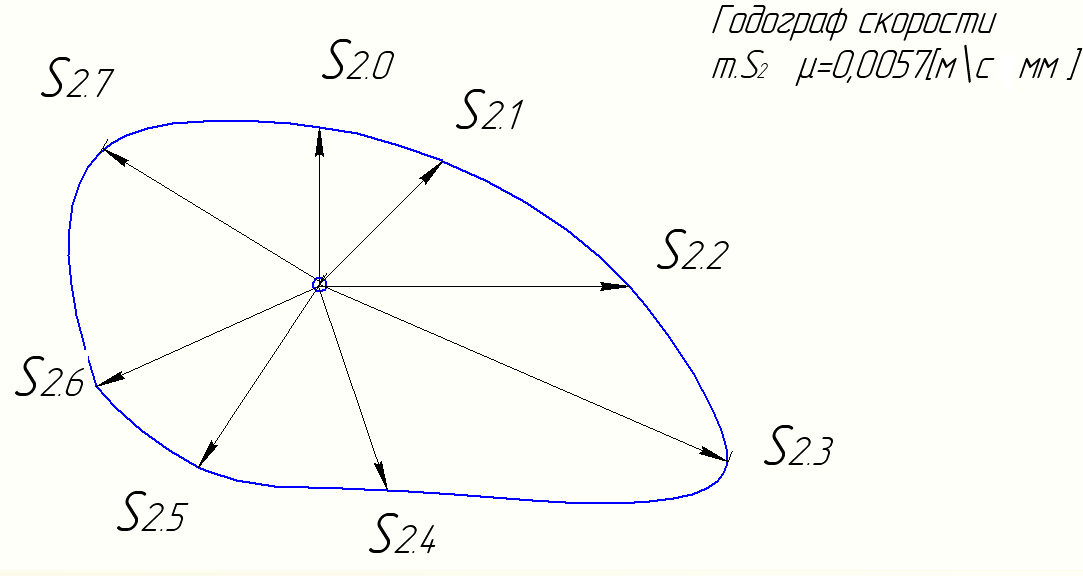
Рис. 8