Опытная проверка распределения максвелла

1. Введение. Понятие о статистическом распределении

Наиболее эффективными при изучении макроскопических систем, состоящих из большого числа частиц (~10²⁵), являются статистические методы. В данной лабораторной работе ставится задача изучить некоторые особенности распределения Максвелла на модели электронного газа, получающегося в электронной лампе. Макросистемы (например, идеальный газ) состоят из большого числа частиц, поведение которых (каждой в отдельности) случайно. Движение молекул идеального газа хаотично, однако в целом макросистема подчиняется определенным закономерностям. Соотношение случайных событий и статистической закономерности можно рассмотреть на модельном опыте с доской Гальтона, которая приведена на рис. 1. – это вертикальная панель, прикрытая спереди стеклом. В верхней части панели в шахматном порядке расположены гвоздики, а в нижней сделаны узкие вертикальные ячейки. Сверху в прибор вставлена воронка, в которой находятся одинаковые (по массе и размером) шарики, нижнее отверстие воронки закрыто заслонкой.

Е сли открыть заслонку, то шарики начнут падать, испытывая при этом столкновения с гвоздиками. При этом поведение отдельного шарика – случайное событие, и он может попасть в любую из ячеек. Однако для большого числа шариков (n – число падающих шариков) количественное распределение по ячейкам или вероятность попадания данного шарика в отдельную ячейку подчиняется статистическому закону (см. рис. 2)

Р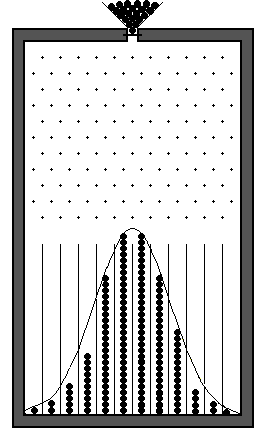 ис. 2. Распределение шариков по ячейкам

после падения 120 шариков

Обозначим координату ячейки, лежащей напротив отверстия воронки за х₀. Видно (см. рис. 2), что чаще всего шарики попадают в ячейки вблизи х₀, и число их уменьшается по мере удаления от х₀. Пусть падало n шариков, тогда n – число шариков попадающих в интервал х. Вероятность (P) попадания шариков в интервал х определяется выражением:

(1)

Если х непрерывно, что возможно при уменьшении диаметров шариков и ширины ячейки, то существует вероятность dP попадания шариков в любой элементарный интервал dx. Ясно, что эта вероятность зависит в общем случае от ширины интервала dx и от того, в окрестности какого значения х (номера ячейки) выбран этот интервал, т.е.

dP=f(x)dx (2)

Функция f(x) называется плотностью вероятности функции распределения случайной величины х. Явный вид этой функции был получен К. Гауссом (Германия) и имеет вид:

(3)

График этой функции представлен на рисунке 3.

Параметр ² – называется дисперсией распределения, а  - средним квадратическим отклонением. Сравнивая результаты опыта, представленного на рис. 2, и вид графика, изображенного на рис. 3, можно заключить, что падение шариков (т.е. поведение в целом макросистемы) подчиняется закону распределения Гаусса, который встречается настолько часто, что получил название нормального закона распределения. В частности, одним из постулатов теории ошибок является утверждение о том, что результат измерения какой-либо физической величины является случайной величиной, распределенной по закону Гаусса.