11. График Мурина.

График Мурина(Никурадзе) У труб с естественной шероховатостью, переход от кривой Блазиуса к кривой для гидравлически шероховатых труб происходит более плавно, без «ложки». • Это объясняется тем, что в трубах с естественной шероховатостью все бугорки имеют различную высоту; их выход из-под вязкого подслоя происходит постепенно. • Поэтому λ изменяется более плавно

1 2. Области линейного сопротивления, переходного режима, доквадратичного сопротивления на графиках Никурадзе и Мурина.

Зона гидравлически гладких труб

Эта зона сопротивления имеет место при небольших числах Re, когда оно находится в пределах

.

В этом случае степень турбулизации потока невелика и вязкий подслой имеет толщину, превышающую величину шероховатости стенок трубы. Поэтому шероховатость не оказывает никакого влияния на турбулентное ядро потока, а потери напора на трение в этой зоне зависят только от числа Рейнольдса. Иными словами, шероховатые трубы в этой зоне сопротивления трения "работают" так же, как гладкие трубы. Коэффициент сопротивления трения в этой зоне можно вычислять по формуле Блазиуса или П.К. Конакова.

Зона переходного сопротивления

Эта зона сопротивления имеет место, когда число Рейнольдса находится в пределах

.

В этой зоне сопротивления вследствие значительной турбулентности поток жидкости частично разрушает вязкий подслой, толщина его становится меньше величины шероховатости, поэтому выступающие за пределы вязкого подслоя "пики" шероховатости оказывают дополнительное сопротивление потоку жидкости. Коэффициент сопротивления трения в этом случае зависит и от числа Рейнольдса, и от величины относительной шероховатости стенок трубы и вычисляется по формуле А.Д.Альтшуля

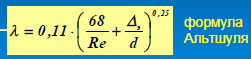
13. Область квадратичного сопротивления на графиках Никурадзе и Мурина. Определения коэффициента сопротивления в этой области.

Зона квадратичного сопротивления

Эта зона сопротивления имеет место при больших числах Рейнольдса, когда оно превышает значение . В этом случае вследствие значительной турбулентности потока толщина вязкого подслоя становится намного меньше величины шероховатости стенок трубы, поэтому её влияние на потери напора становится преобладающим. Возрастание числа Рейнольдса не приводит к увеличению потерь напора, так как степень турбулентности потока жидкости в этой зоне имеет предельное значение, т.е. наступает автомодельный режим сопротивления. Коэффициент сопротивления трения для этой зоны вычисляют по эмпирической формуле Б.Л. Шифринсона

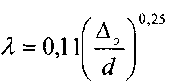Границы зон сопротивления трения по числу Рейнольдса и определены по результатам многочисленных опытов разных авторов и округлены.

14 Теорема Борда.

- теорема Борда (1766)

Теорема Борда - потеря напора при внезапном расширении русла равна скоростному напору, определенному по разности скоростей

15. Определение путевых потерь для труб с естественной и искуственной шероховатостью.

В одних случаях потери напора распределяются по длине трубопровода - это линейные (путевые) потери;

Изучение движения жидкости по шероховатым трубам в области, где потери напора определяются только шероховатостью стенок труб, и не зависят от скорости движения жидкости, т.е. от числа Рейнольдса осуществлялось Прандтлем и Никурадзе. В результате их экспериментов на моделях с искусственной шероховатостью была установлена зависимость для коэффициента Дарси для этой так называемой квадратичной облас­ти течения жидкости:

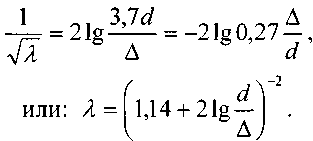
Для труб с естественной шероховатостью справедлива формула Шифринсона

где: - эквивалентная величина выступов шероховатости. Ещё более сложная обстановка связана с изучением движения жидкости в переход­ной области течения, когда величина потерь напора зависит от обоих факторов,