1.6. Распределение интенсивности в интерференционной картине от двух щелей
Интерференционная картина, созданная когерентными световыми волнами от мнимых источников S1 и S2, имеет вид чередующихся светлых и темных полос. При этом максимумы (середины светлых полос) возникают под углами , удовлетворяющими условиям максимумов интерференции (дифракция Фраунгофера на двух щелях, расстояние между которыми d):
d·sin = m, m = 0, ±1, ±2,… ,
а минимумы (середины темных полос) под углами , удовлетворяющими соотношению:
d·sin = (m+1/2).
Рассмотрим распределение интенсивности света в интерференционной картине.
Если расстояние L от источников до экрана велико по сравнению с расстоянием d между щелями (L≫d) (см. рис.2) и при этом рассматривать только точки Р, отстоящие от центра 0 интерференционной картины на расстояние y, малое по сравнению с L (y≪L), тогда sin = y/L и разность фаз волн от источников S1 и S2 составит:
.
В этом случае зависимость интенсивности на экране от координаты y для бесконечно узких щелей S1 и S2 описывается функцией:
.
(27)
Распределение интенсивности, согласно формуле (27), в зависимости от координаты y на экране представляет собой чередование максимумов одинаковой высоты (см. рис.8b). Однако данный результат не применим к случаю реальных щелей, шириной которых нельзя пренебречь.
Дифракция ослабляет интенсивность вторичных интерференционных максимумов (световых полос), в результате они не имеют одинаковой высоты.
Распределение интенсивности света на экране с учетом дифракции:
,
(28)
где I – интенсивность под углом ,
I0 – интенсивность в центре интерференционной картины,
D – ширина щели,
– разность фаз волн от верхнего и нижнего краев одной щели,
,
– разность
фаз волн от щелей S1
и S2
,
,
d – расстояние между центрами щелей.
Зависимость интенсивности I, согласно формуле (18), представляет собой произведение трех множителей: первый – интенсивность I0 центрального максимума, второй – дифракционный множитель, третий – интерференционный множитель (совпадает с величиной соответствующего множителя в формуле (17)).
На
рис.8 показаны графики дифракционного
(рис.8а) и интерференционного множителя
(рис.8b)
соответственно, а также график
результирующей интенсивности I (рис.8с),
как функции угла ,
согласно формуле (18), для случая
.
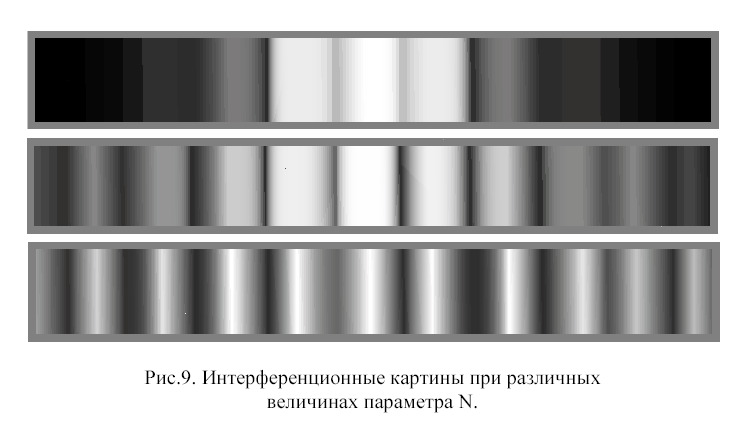
Штриховая линия на рис.8с показывает, что дифракционный множитель ведет себя подобно огибающей интерференционных пиков. По мере удаления от центра наблюдается заметное убывание интенсивности интерференционных полос. На рис. 9 показаны интерференционные картины, наблюдаемые на экране при различных значений параметра N.
Первый минимум на дифракционной картине отвечает условию:
,
а так как d = 6D (рис.8), то d·sin = 6. Интерференционные максимумы отвечают условию:
d·sin = m·,
следовательно, на рис.8 дифракционный минимум отвечает интерференционной полосе с m = 6 и соответствующий пик интенсивности не возникнет. В этом случае на экране будет наблюдаться центральный максимум (m = 0) и по пять максимумов с каждой стороны (m = 1,…, 5), всего 11 светлых полос.
Таким образом, максимальный порядок интерференционного максимума mmax, наблюдаемый на экране, связан с шириной щели D соотношением:
.
(29)