4.1 Описание системы

Структурная схема исследуемой линейной системы представлена на рисунке 2.1.

Рисунок 2.1

W₀(s)= , W₁(s)= , где W₀(s) - неустойчивый объект управления (O2), W₁(s) - инерционно-форсирующий регулятор (P2), К₀- коэффициент передачи звена, T₀, Т₁, Т₂- постоянная времени, Kр - усилитель сигнала ошибки.

Параметры системы - Kр=4.6, K₀=10,T₀=0.46 c,T₁=0.01c, Т₂=0.1 с.

4.2 Характеристическое уравнение

Составим характеристическое уравнение системы, для этого найдем передаточную функцию разомкнутой системы:

Wр(s)= = .

Тогда характеристическое уравнение системы:

Q(s)+R(s)=0,

T₀T₁s³+ (T₀-T₁)s² + (K_PK₀T₂ -1)s + K_PK₀ =0- порядок системы равен трем (n=3, a₀s³ + +a₁s² +a₂s + a₃=0).

Рассчитаем значения коэффициентов характеристического уравнения:

a₃=K_pK₀=46, a₂=K_PK₀T₂ -1=3.6, a₁=T₀-T₁=0.45, a₀=T₀T₁=0.0046.

Характеристическое уравнение запишется:

0.0046s³+ 0.45s² +3.6s + 46=0.

4.3 Проверка устойчивости системы по алгебраическому критерию

Воспользуемся критерием Гурвица, согласно которому для устойчивости системы необходимо и достаточно, чтобы диагональные миноры матрицы Гурвица были устойчивы (при положительности коэффициентов характеристического уравнения).

Составим матрицу Гурвица:

Г=

Тогда должны выполнятся условия:

a₀>0, a₁>0, a₂>0, a₃>0,

a₁a₂>a₀a₃.

Подставив числовые значения, получим:

0.0046>0, 0.45>0, 3.6>0, 46>0,

0.453.6>0.004646, 1.62>0.212.

Очевидно, что рассматриваемая система устойчива.

4.4 Проверка устойчивости системы по критерию Михайлова

Составим функцию Михайлова:

характеристическое уравнение – Ф(s)= 0.0046s³+ 0.45s² +3.6s + 46, тогда функцию Михайлова получим заменой s на jω – M(jω)= 0.0046( jω)³+ 0.45( jω)² + 3.6(jω)¹ + 46=

=46-0.47ω² +j(5.6ω-0.0046ω³). Заметим что порядок системы равен трем (n=3).

Годограф функции Михайлова представлен на рисунке 4.2.

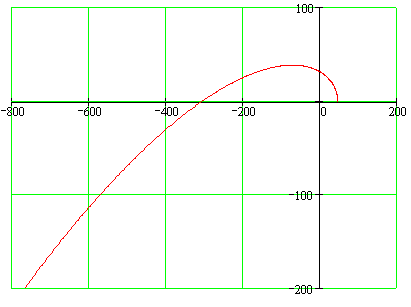
Рисунок 4.2

Как видим, при изменении частоты от 0 до  вектор кривой Михайлова начав своё движение на вещественной полуоси, последовательно проходит три квадранта (для системы третьего порядка), нигде не обращаясь в нуль. Согласно критерию Михайлова система устойчива.

4.5 Проверка устойчивости по критерию Найквиста

Определим устойчивость разомкнутой системы. Характеристическое уравнение разомкнутой системы – R(s)= . Корни характеристического уравнения – s₁=0; -1+s₂T₀=0, s₂=1/T₀=2.174; 1+s₃T₁=0, s₃=-1/T₁=-100. Согласно теореме Ляпунова о неустойчивости, разомкнутая система не устойчива, так как характеристическое уравнение имеет два правых корня. Данная система является астатической с астатизмом первого порядка =1 (один нулевой корень).

Передаточная функция разомкнутой системы W_р(s)= .

W(jω)=U(ω)+jV(ω), где

U(ω)= ,

V(ω)= .

Годограф АФЧХ представлен на рисунке 4.3.

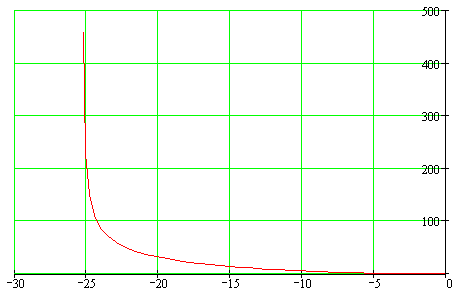
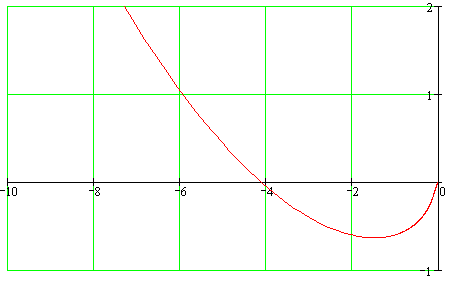
Рисунок 4.3

Так как разомкнутая система неустойчивости, то для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф Найквиста, дополненный на участке разрыва дугой ν = 1 = бесконечно большого радиуса, не охватывал точку (-1;j0 ), т.е. чтобы разность между числом положительных и отрицательных переходов на отрезке вещественной оси (-∞; -1) была равна =1, где -число правых корней . Из рисунка 4.3 видно, что годограф Найквиста, дополненный на участке разрыва дугой ν = 1 = бесконечно большого радиуса, не охватывает точку (-1;j0 ) (разность между числом положительных и отрицательных переходов равна 0), т.е. система устойчива.

Определим устойчивость системы по критерию Найквиста для логарифмических характеристик.

L()= ,

()= –  + arctg T₂ – ( – arctg T­₀) – arctg T₁.

Графики ЛАХ и ЛФХ представлены на рисунке 4.4.

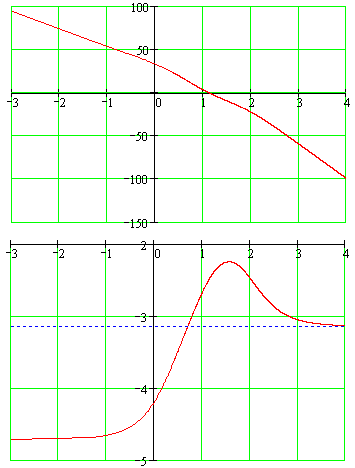
Рисунок 4.4

Как видим из рисунка, разность между числом положительных и отрицательных переходов частотной характеристики уровня –π(2i+1) (i=0,1,2…) в области, где амплитудная характеристика больше нуля, равна 1. Можно сделать вывод, что система устойчива.

4.6 Граничное значение коэффициента усиления K_гр

Характеристическое уравнение для системы 3-го порядка:

a₀s³ + a₁s² + a₂s + a₃ = 0

K_PK₀ + (K_PK₀T₂ - 1)s + (T₀ - T₁)s² + T₀T₁s³ =0,

a₃=K_pK₀=46, a₂=K_PK₀T₂ + 1=3.6, a₁=T₀-T₁=0.45, a₀=T₀T₁=0.0046,

0.0046s³+ 0.45s² +3.6s¹ + 46=0.

Согласно критерию устойчивости Гурвица, система третьего порядка будет устойчива, если выполняются следующие неравенства:

a₀>0, a₁>0, a ₂>0, a₃>0, a₁a₂ – a₀a₃>0.

Т.к. коэффициенты характеристического уравнения положительны, то должно выполнятся условие (T₀ - T₁)( K_PK₀T₂ - 1) – K_PK₀T₀T₁>0, откуда

K_гр= = =1.11.

4.7 Граница области устойчивости

Границу области устойчивости в плоскости параметров (К_Р; T₁) построим исходя из найденной выше формулы - K_гр(Т₁)= = . На рисунке 4.5 представлен график расчетной границы области устойчивости c отметками экспериментальных точек.

В таблице 4.1 представлены экспериментальные данные.

Таблица 4.1 Экспериментальные данные

	1 опыт-система устойчива	2 опыт-система не устойчива	3 опыт - колебательная граница устойчивости
Kp	4.6	2.6	1.3	1.5	1.1	3.3	5.8
T1	0.01	0.2	0.02	0.03	0.01	0.01	0.07

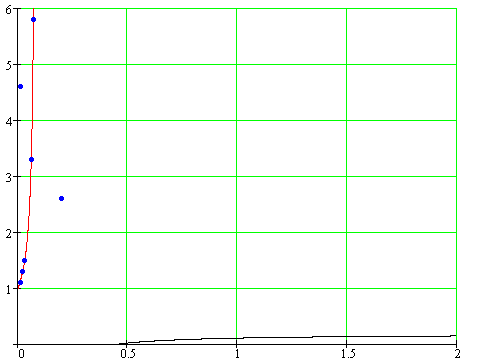
Рисунок 4.5

Из рисунка видно, что при параметрах K_p=4.6, Т₁=0.01 система устойчива, что было подтверждено в ходе исследования системы на устойчивость, при параметрах K_p=2.6, Т₁=0.2 - неустойчива.

Вывод

Исходя из проведенных исследований системы по критериям Гурвица, Михайлова, Найквиста можно сделать вывод, что система устойчива. Данная система является условно устойчивой, так как уменьшение коэффициента усиления приводит к неустойчивости системы.