П ример 4

Построить эпюры поперечной силы Q и изгибающего момента М для балки, показанной на рис. 5, определить размеры круглого, прямоугольного (h/b =2) и двутаврового сечения. Проверить прочность двутавра по главным напряжениям, если:

Дано: F₃ = 40 кН, М ₂= 20 кН∙м, q₁ =15 кН/м, а = 1,4 м. [] = 150 МПа, [] = 150 МПа

Рисунок 4.

Для нахождения реакций опор R_A и R_C воспользуемся уравнениями равновесия для плоской параллельной системы сил.

1.

2. 

Из уравнения 1

Из уравнения 2

Проверка

Согласно условию равновесия плоской системы сил должно выполняться следующее условие:

,

.

Условие выполняется. Значит, составили уравнения равновесия и решили их верно.

Разбиваем рассматриваемую балку на участки АC, СD, DB.

Определяем значения поперечной силы и изгибающего момента на данных участках.

Участок

при

кН

Участок

при кН;

при

при

при

Участок

кН;

;

при кН ;

при

Найдем экстремум изгибающего момента на участке CD. Для этого значение поперечных сил на этом участке приравняем к 0 и выразим координату z_exr, при которой, а момент имеет экстремальное (в данном случае -минимальное) на этом участке значение. Далее подставим z_exr в уравнение момента на этом участке и найдем

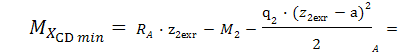
Для балки, изображенной на рис. 5 определить размеры круглого, прямоугольного (h/b = 2) и двутаврового сечения. Проверить прочность двутавра по главным напряжениям, если [] = 150 МПа, [] = 150 МПа.

Определяем из условия прочности необходимый момент сопротивлении

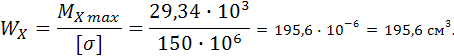
Из уравнения момента сопротивления круга определяем размеры сечения.

Выбираем

Определяем размеры прямоугольного сечения

; для соотношения h/b = 2

Принимаем

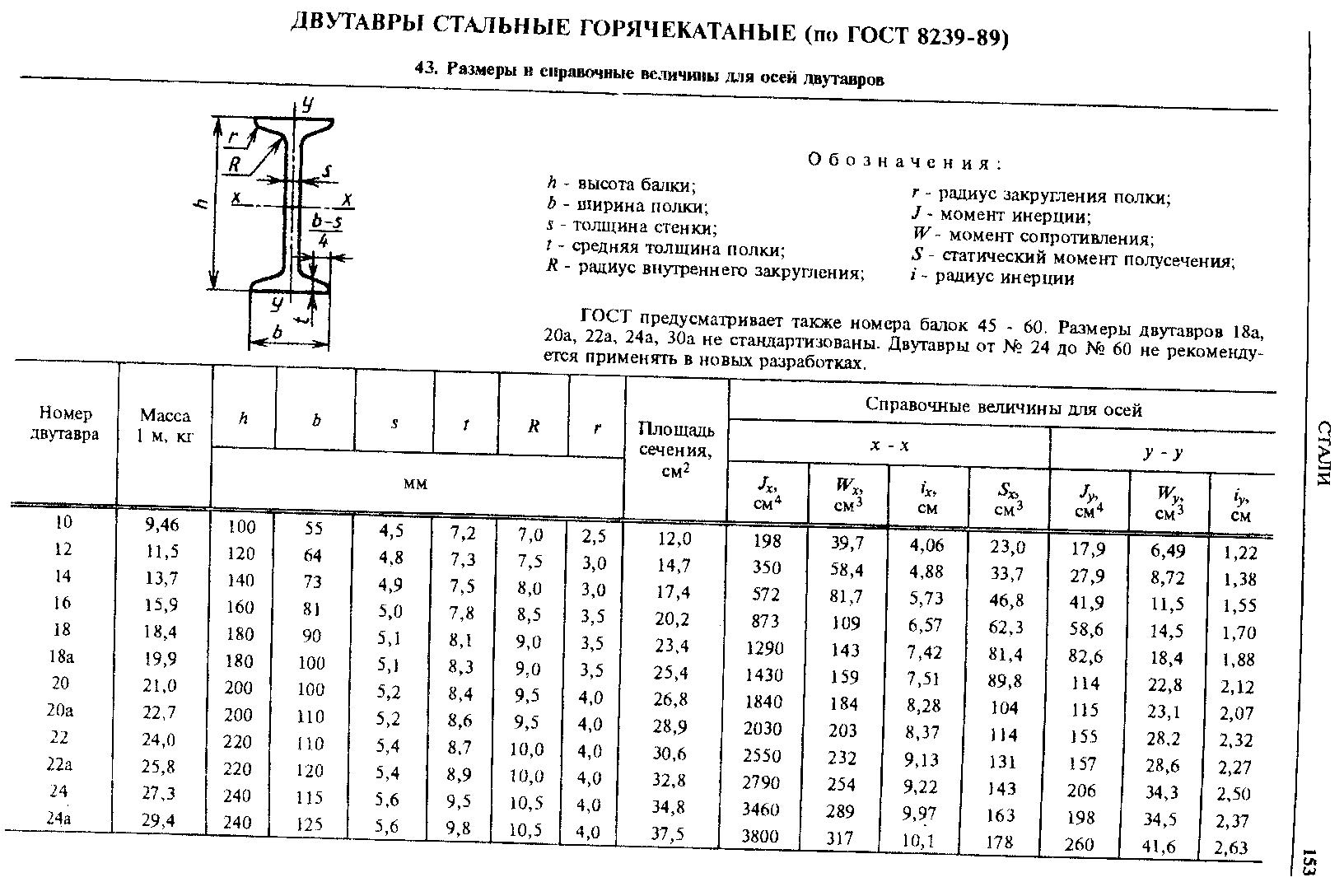
Подбираем по сортаменту двутавровую балку № 20а (ГОСТ 8239-89)

W_X = 203 см³, S_X^* =114 см³, I_X = 2030 см⁴, h = 200 мм, b = 110 мм, d = 5,2 мм, t = 8,6 мм.

Для проверки прочности балки по главным напряжениям, необходимо построить эпюры нормальных и касательных напряжений в опасном сечении. Так как величина главных напряжений зависит и от нормальных и от касательных напряжений, то проверку прочности следует произвести в том сечении балки, где и достаточно велики. Для нашего случая и поперечная сила изгибающий момент имеют максимальные значение в одном сечении балки – сечении С. , и поэтому оно наиболее нагружено.

Нормальные напряжения, изменяясь по высоте сечения, подчиняются линейному закону:

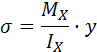
где y – координата точки сечения (рис. 24).

при у = 0,  = 0;

при

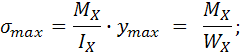
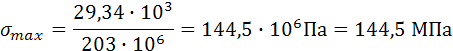
Закон изменения касательных напряжений определяются законом изменением статического момента площади, который, в свою очередь изменяется по высоте сечения по параболическому закону. Вычислив значение для характерных точек сечения, построим эпюру касательных напряжений. При вычислении значений  воспользуемся обозначениями размеров сечения, принятыми на рис. 17.

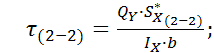
где

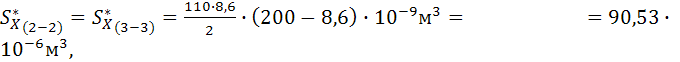тогда

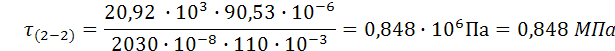
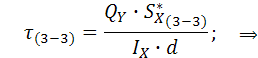
где

Как видно из эпюр, опасным в сечении является слой 3–3, где нормальные и касательные напряжения имеют значения близкие к максимальным, в то время как в слое 1–1, где ,  = 0, а в слое 4–4, где ,  = 0.

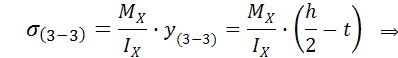
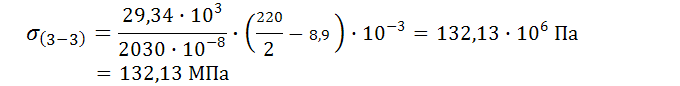
Определяем главные напряжения по третьей теории прочности по формуле:

=

условие прочности для слоя 3–3 выполняется

Таблица 7

Исходные данные к задаче № 4

№	а, м	q1=q3, кН/м	q2, кН/м	F1, кН	F2, кН	F3, кН	М1, кН∙м	М2, кН∙м	М3, кН∙м	№ схемы
1	1,8	12	30	40	35	10	15	35	10	1
2	1	10	25	15	30	20	15	30	20	2
3	1,2	15	20	20	25	30	20	25	30	3
4	1,4	20	15	25	20	40	25	20	40	4
5	1,6	25	10	30	15	10	30	15	10	5
6	1,8	30	5	35	10	20	35	10	20	6
7	2	25	30	40	5	30	40	5	30	7
8	0,8	10	25	10	35	40	10	35	40	8
9	1	15	20	15	30	10	15	30	10	9
0	1,6	10	25	20	15	20	30	25	20	10

Таблица 8

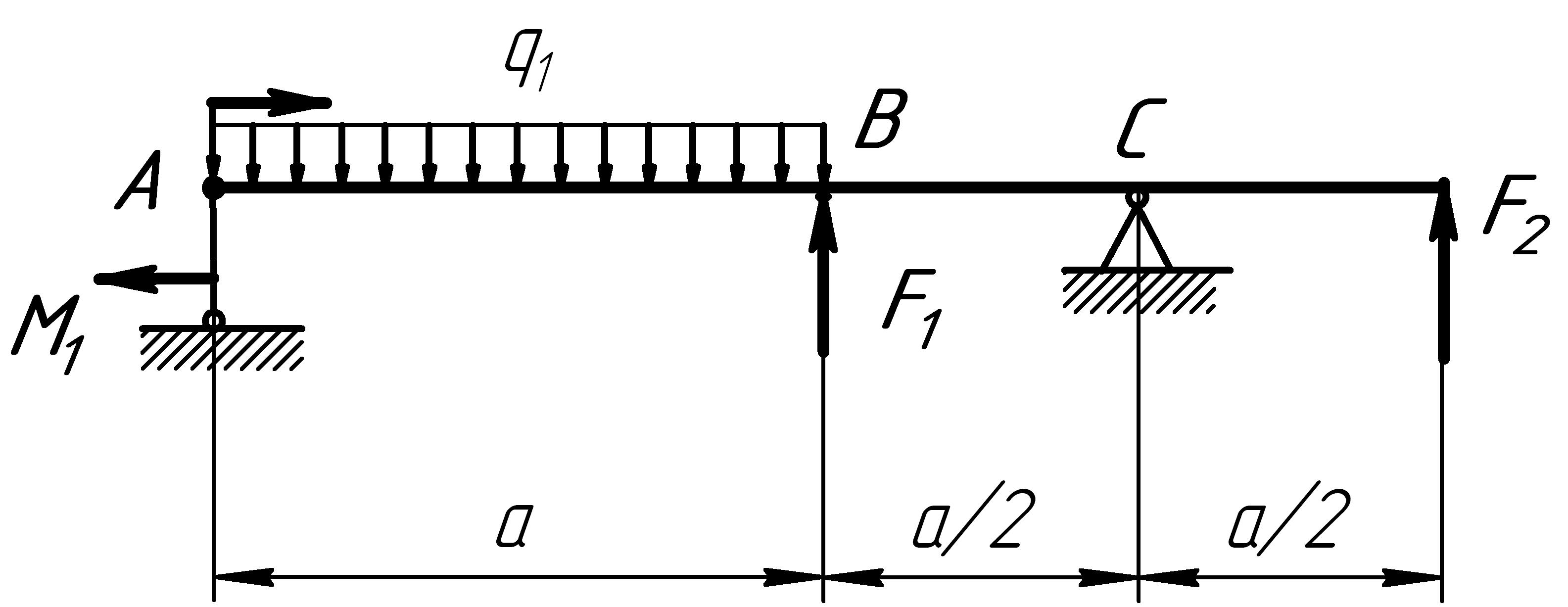
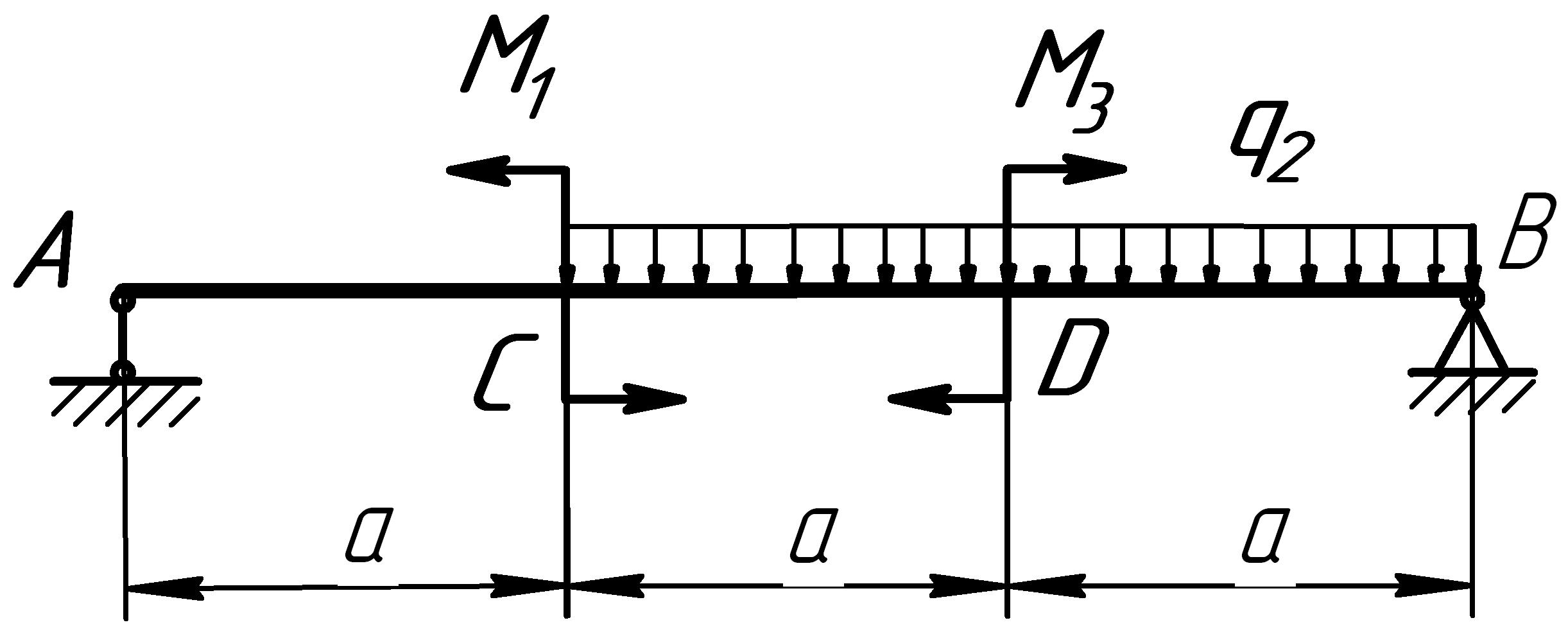
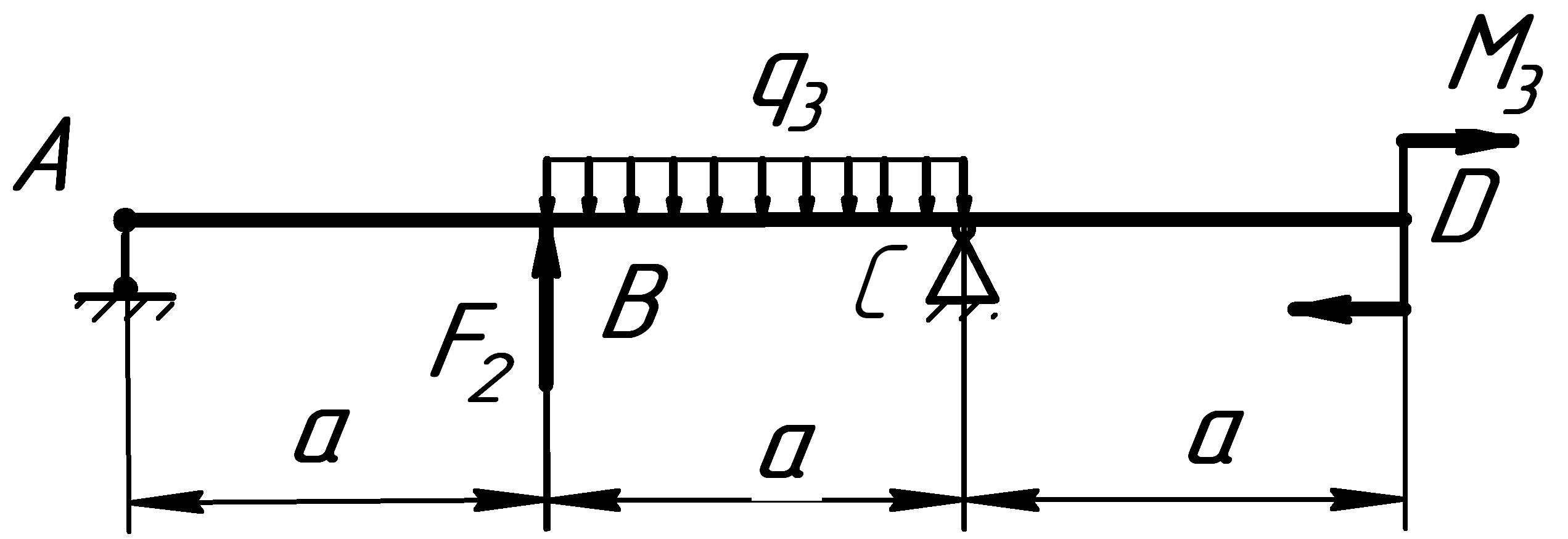
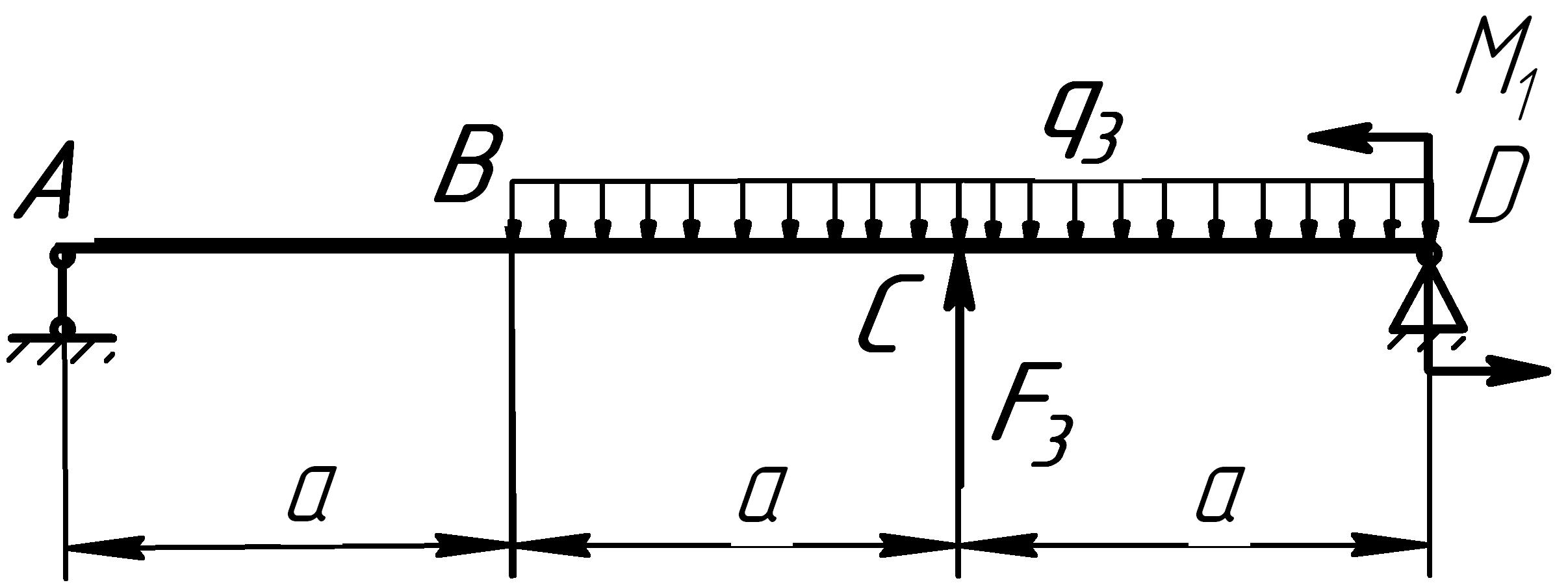
Расчетные схемы к задаче № 6

1		6
2		7
3		8
4		9
5		10