Решение

Разбиваем брус на участки АВ, ВС, CD (см. рис. 1)

Последовательно определяем значения нормальной силы ,нормального напряжения , и удлинения на каждом участке начиная со стороны не закрепленного участка.

Участок АВ,

(знак т.к. стержень на участке АВ действием силы растянут);

Па 25 МПа;

м мм мкм

Участок ВС,

при

при

при , Па 12,5 МПа;

при , Па МПа;

м м мм = 20,83 мкм

Участок СD,

;

Па 12,5 МПа ;

м мм мкм

Строим эпюры изменения нормальной силы и нормального напряжения (рис. 4)

Определяем суммарное изменение длины стержня удлинение стержня

;

Таблица 3

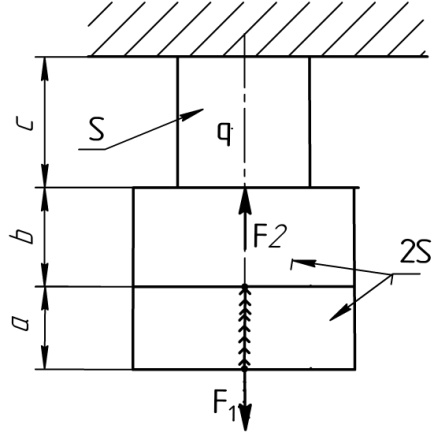
Исходные данные к задаче № 2

№ п/п	а, м	b, м	c, м	q, кН/м	F1, кН	F2, кН	S, см2	номер данных
1	0,6	1,0	0,4	30	10	35	8,2	1
2	0,8	1,2	0,6	25	15	30	10,4	2
3	1	1,6	0,8	20	20	25	8,6	3
4	1,2	1,8	1,0	15	25	20	6,8	4
5	1,4	2,0	1,2	10	30	15	5,8	5
6	1,6	2,2	1,4	5	35	10	6,0	6
7	1,8	2,0	1,6	30	40	5	7,2	7
8	2	2,2	1,8	25	10	35	6,8	8
9	1	1,4	0,5	20	15	30	7,6	9
0	1,2	1,6	0,8	15	20	25	8,4	10
	а	д		в	г	б	в	д

Таблица 4

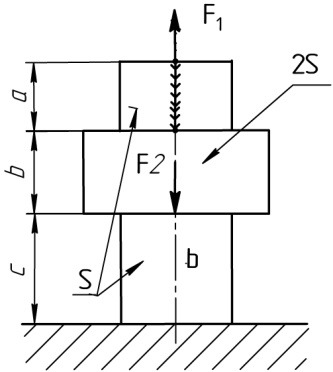
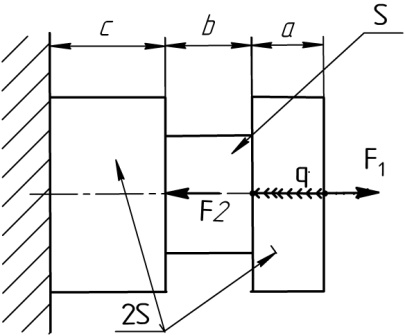
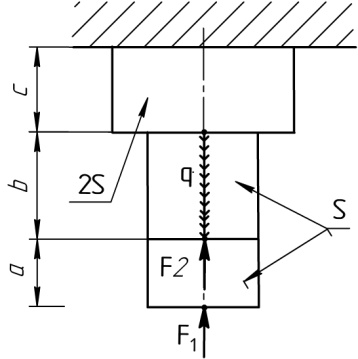
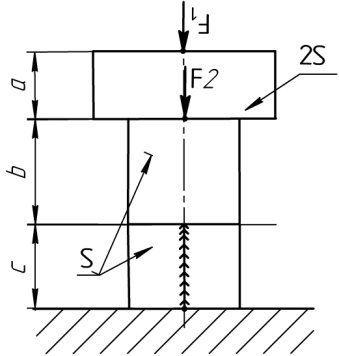
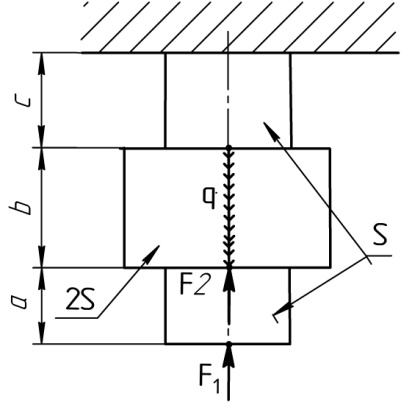
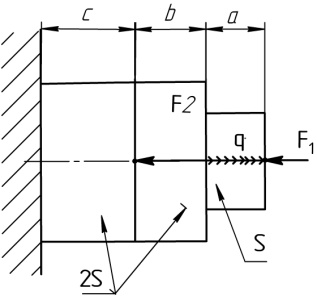
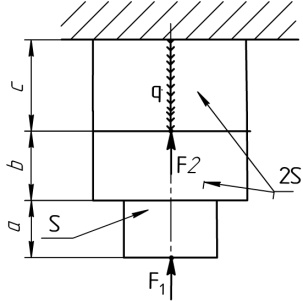
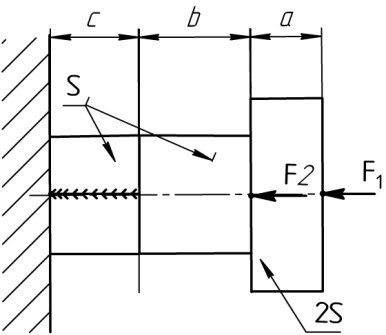
Расчетные схемы к задаче №2

1		2
3		4
5		6
7		8
9		10

.

Указания к задаче 3

Кручение – это такой вид деформации стержня, при котором в его поперечных сечениях возникает единственный внутренний силовой фактор – крутящий момент.

Внешние моменты, воздействующие на вал, называются скручивающими.

Расчет вала на прочность начинается с построения эпюры крутящего момента и отыскания опасного сечения.

Касательные напряжения при кручении определяются по формуле:

,

где Т_КР – крутящий момент, действующий в сечении;

 - радиус той точки поперечного сечения, в которой определяются напряжения;

I_p – полярный момент инерции сечения.

Условие прочности при кручении записывается следующим образом:

.

где W_p – полярный момент сопротивления сечения.

Угол закручивания вала определяется по формуле:

,

где l – длина вала;

G – модуль упругости второго рода.

Условие жесткости при кручении записывается следующим образом:

.

Полярный момент инерции и полярный момент сопротивления круглого сечения определяются по формулам соответственно:

, ,

где d – диаметр вала.

Полярный момент инерции и полярный момент сопротивления кольцевого сечения определяются по формулам соответственно:

, ,

где D – внешний диаметр вала;

d – внутренний диаметр вала.

ПРИМЕР

Для вала, изображенного на рис. 5, подобрать поперечное сечение круглой, кольцевой и прямоугольной форм, если M₁ =400 Нм, M₂ =800 Нм, M₃ = 500Нм, M₄ = 700 Нм, M₅ =200Нм,  = 0,7, h/b = 1,4, [] =80 МПа., a = 0,5 м, b=0,4 м, c = 0,3 м. Построить эпюру углов закручивания для вала круглого поперечного сечения.

Решение

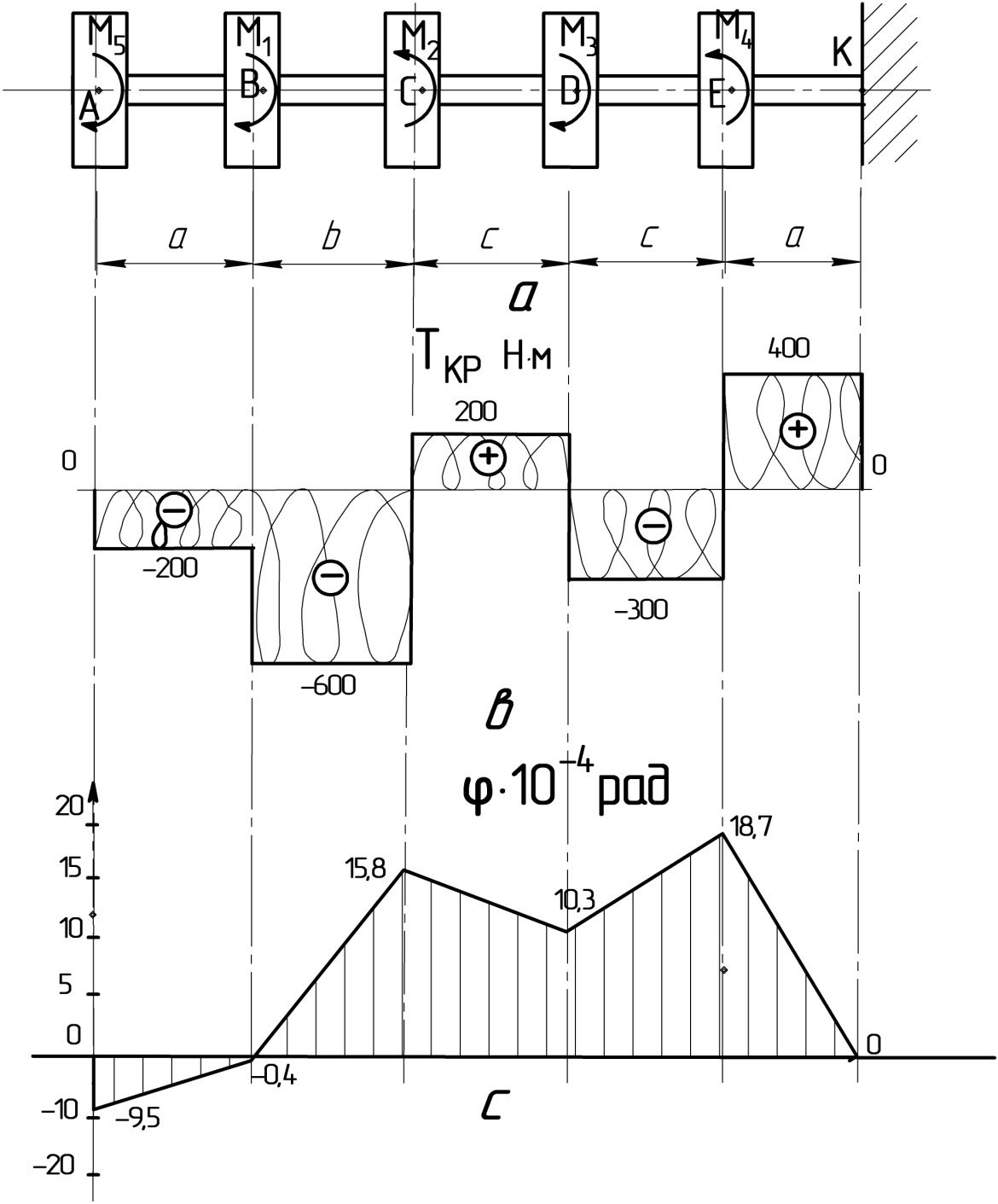
Рис. 4

Строим эпюру крутящего момента со свободного конца вала и определяем опасное сечение ( cм. рис 4).

Участок АВ

200 Н·м;

Участок ВС

200 400 = 00 Н·м;

Участок СД

200 400 800 = 200 Н·м;

Участок ДЕ

Участок ЕК

=

Из эпюры крутящих моментов (рис. 4b) видно, что опасным, является II участок СВ, максимальное значение крутящего момента Т_{кр max}= 600 Н м.

Подбираем поперечное сечение вала

3.1) Круглое сечение

Условие прочности при кручении:

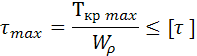
где - момент сопротивления сечения,

= =3,34·10^-2 м.

Принимаем d = 34 мм.

3.2) Кольцевое сечение

= 3,67·10^-2 м;

Принимаем D = 38 мм, тогда d = 0,7·38 = 26,6 мм, принимаем 26 мм.

3.3) Прямоугольное сечение

где для прямоугольного сечения с отношением h/b = 1,4 коэффициент  = 0,3184.

= 0,0236 = 2,36·10^-2 м = 23,6 мм

h = 1,4·b, h = 1,4 · 0,0236 =0,03304= 3,304·10^-2 м = 33,2 мм.

Сравним веса валов с различными вариантами конфигураций сечения

Найдем площади поперечного сечения для каждого из валов: круглого, кольцевого, прямоугольного.

Для круглого - = 9,08·10 ^{– 4} м²

Для кольцевого -

= 6,03·10 ^{– 4} м²

Для прямоугольного -

=2,36·10^-2 ·3,32·10^-2 = 7,84·10 ^{– 4} м²

Сравниваем площади сечений

Для заданных геометрических соотношений элементов валов, вес вала круглого сечения будет приблизительно на 34 процента больше чем у кольцевого и на 30 процентов меньше чем у прямоугольного.

Вывод. Для передачи крутящих моментов с точки зрения экономии металла выгоднее применять валы кольцевого сечения.

Строим эпюру углов закручивания вала круглого сечения (рис 4с).

Для вала круглого сечения угол закручивания определяется по формуле:

;

- крутящий момент на рассматриваемом участке;

– длина участка;

– модуль упругости 2-го рода для заданного материала. Для нашего случая Па;

- момент инерции сечения.

Для круглого сечения . .

м⁴

Вычисление углов закручивания начинаем с участка ЕК, т.е. с участка ближайшего креплению конца вала

= 0,0187 рад;

рад;

Тогда суммарный угол закручивания участка DK отношению к заделке составит:

0,0103 рад;

рад;

Тогда суммарный угол закручивания участка СK отношению к заделке

составит:

Тогда суммарный угол закручивания участка BK по отношению к заделке составит:

0,0004 рад;

рад;

Тогда суммарный угол закручивания участка AK, то есть полный угол закручивания всего вала по отношению к заделке составит:

0,0095 рад