Интегрирование функций.
Неопределенный интеграл.
Определение неопределенного интеграла.
Восстановление функции по известной производной этой функции называется интегрированием функции.
Функция F(x) называется первообразной для функции f(x) на некотором отрезке [а;в] если для всех значений х на данном отрезке выполняется равенство F(x) = f(x).
Множество всех функций, производные которых равны f(x), обозначается символом
f(x)dx
и называется неопределенным интегралом от функции f(x).
В данной формуле по определению:
f(x) – подинтегральная функция,
f(x)dx – подинтегральное выражение.
Если F(x) – первообразная для функции f(x), то множество функций
F(x) + C будет неопределенным интегралом от функции f(x), т.е.:
f(x)dx = F(x) + C,
где С – произвольная постоянная.
Свойства неопределенного интеграла.
Из определения неопределенного интеграла вытекают следующие его свойства.
1. Производная неопределенного интеграла равна подинтегральной функции:
f(x)dx = F(x) + C = F(x) = f (x)
2. Постоянный множитель можно выносить за знак неопределенного интеграла:
K f(x)dx = K f(x)dx
3. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
dF(x) = F(x) + C
4. Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций в отдельности:
(f(x) g(x))dx = f(x)dx g(x)dx
Таблица основных интегралов.
Нижеприведенная таблица неопределенных интегралов получена либо из сравнения с таблицей производных из понимания того, что интегрирование – процедура, обратная дифференцированию, либо непосредственным дифференцированием правой части формулы. Таблица очень краткая и приведена в качестве иллюстрации.
-
№
п/п
f(x)dx= F(x) + C
1
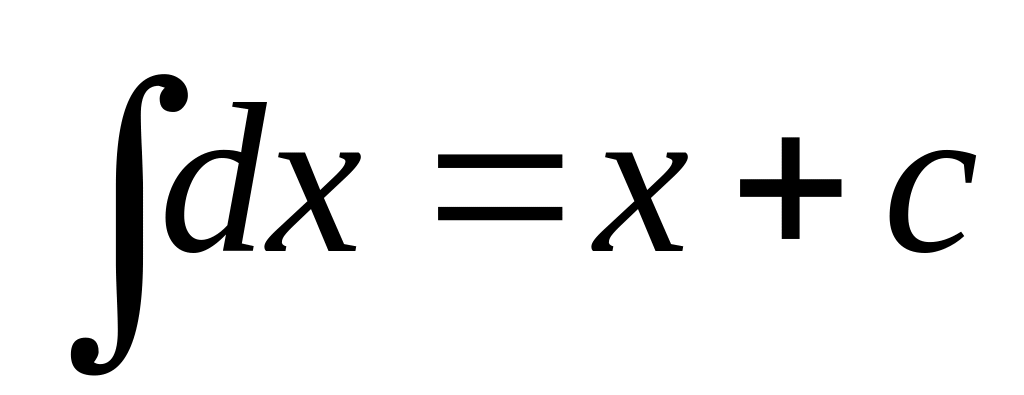
2
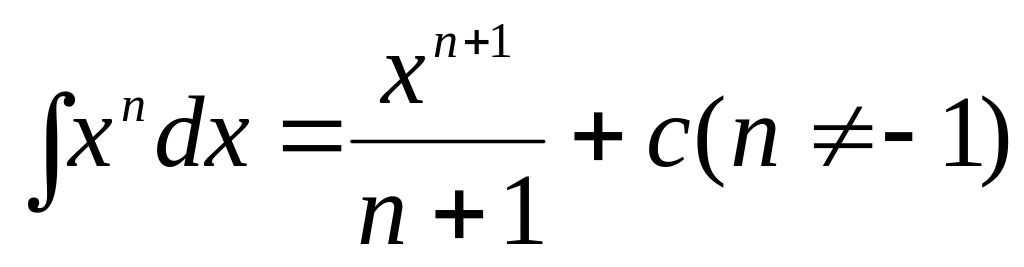
3
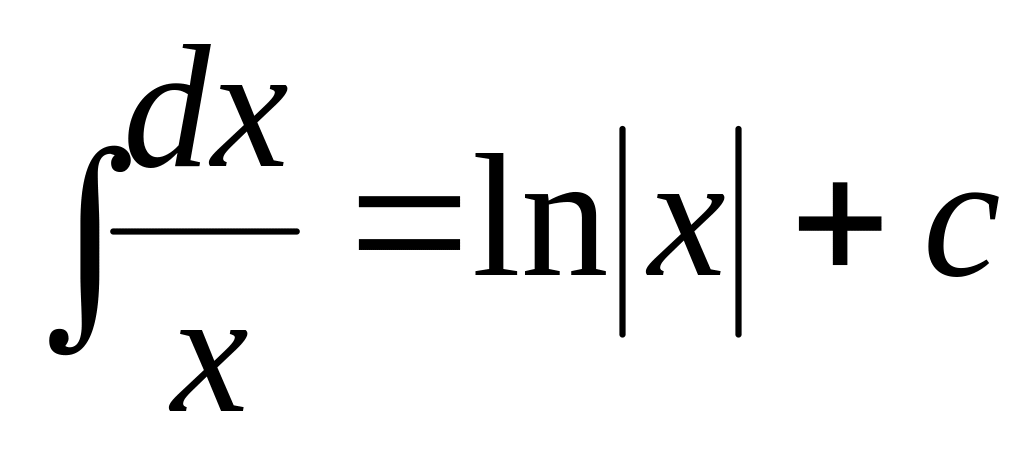
4
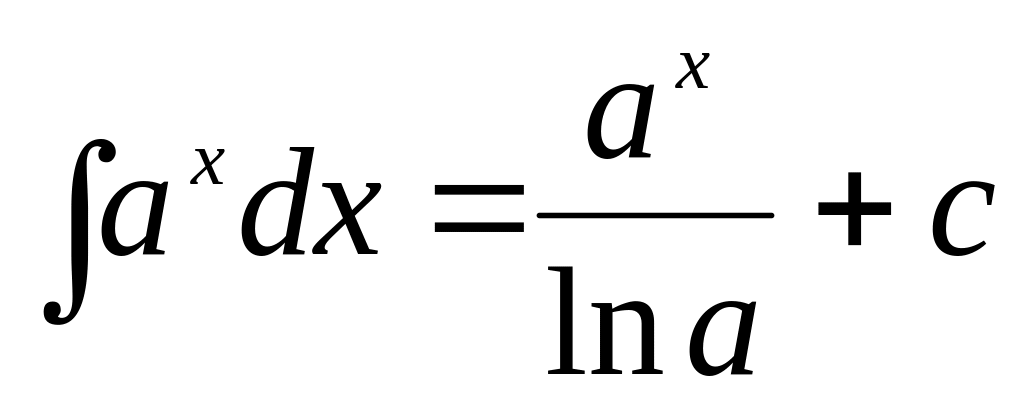
5
∫
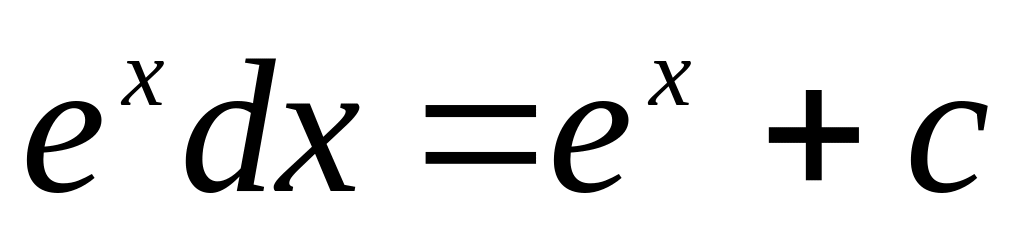
6
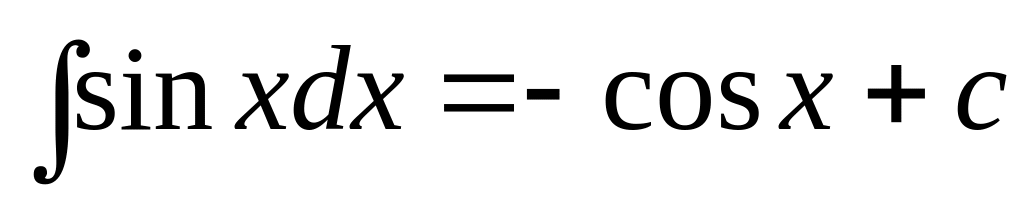
7
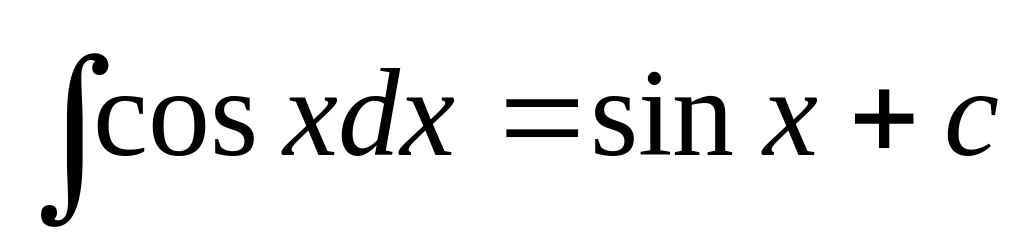
8
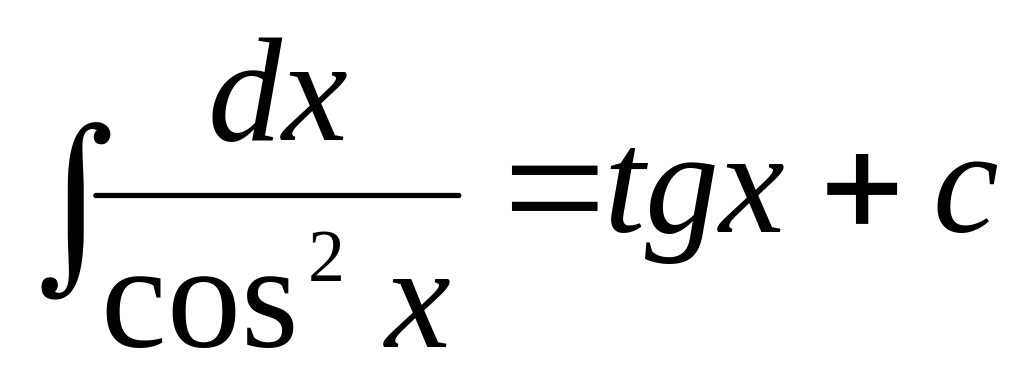
9
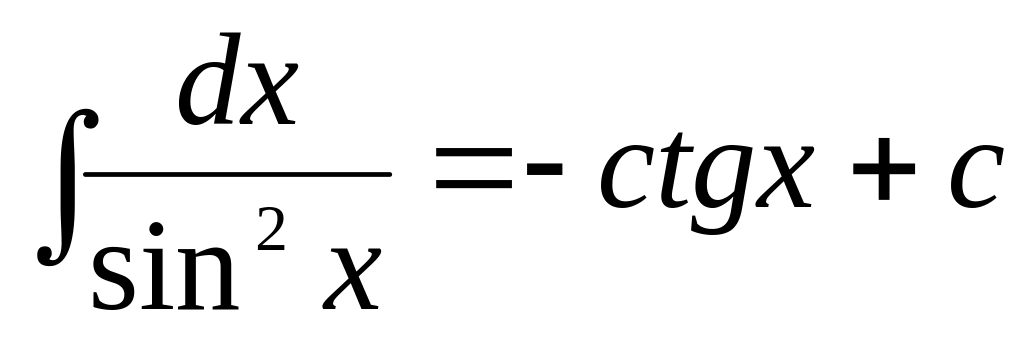
10
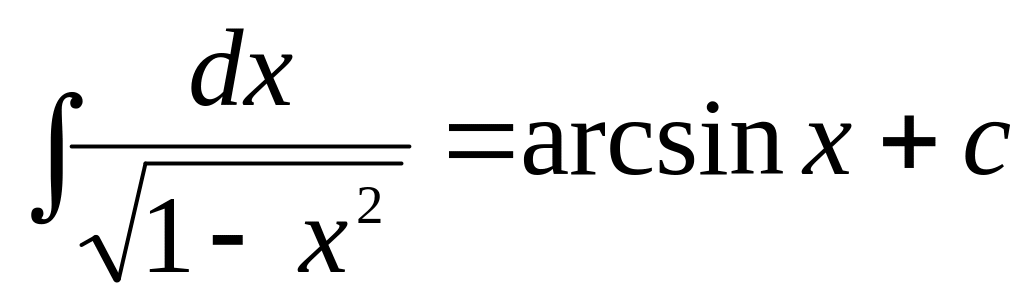
11
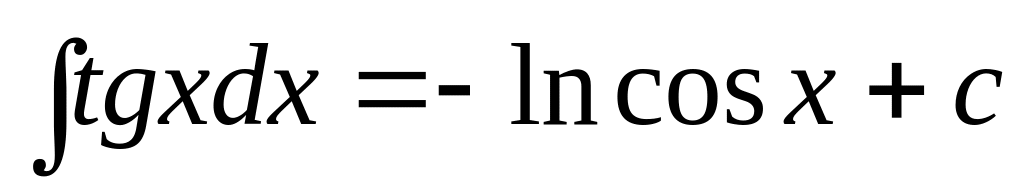
Основные методы интегрирования.
Нахождение неопределенного интеграла – сложная математическая задача, нет единого универсального метода, который позволил бы решить данную задачу. По алгебраическому виду интеграла его можно отнести к определенному классу интегралов, для которых метод нахождения неопределенного интеграла разработан. Хотя существует много различных методов интегрирования, все они основаны на преобразовании (приведении) первоначального интеграла к табличному виду. Рассмотрим некоторые из простых методов.