Ускорение

Неравномерность движения (в Ф const) характеризуется фи­зической величиной — ускорением.

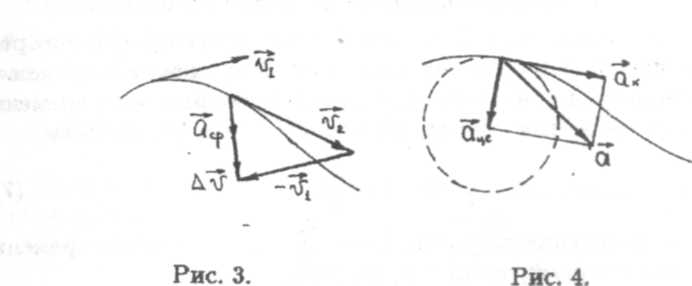
Пусть материальная точка за малый промежуток времени At из точки А, где она имела скорость v_b переместилась в точ­ку В, где она имела скорость v₂ (рис. 3). Изменение скорости есть вектор Av, равный разности векторов конечной и началь­ной скоростей, т.е. v = v₂ — v₁.

Отношение изменения вектора скорости к тому промежут­ку времени, за который это изменение произошло, называется средним ускорением.

a_ср= (4)

В общем случае среднее ускорение может быть различным на различных участках траектории и при t 0 оно превращается в мгновенное ускорение. Для наглядности ограничимся случа­ем плоской кривой. Тогда мгновенное ускорение — это вектор направленный под углом к траектории в сторону ее вогнутости, а по модулю равный пределу отношения изменения скорости Av к промежутку времени At при стремлении At к нулю (рис. 3)

a= = = = v (5)

Согласно формулам (4) и (5), ускорение измеряется в (м/с2).

Полное ускорение а принято раскладывать на две составля­ющие (рис. 4), одна из которых направлена по касательной к траектории и называется касательным или тангенциальным ускорением (аг), другая - по нормали и называется нормаль­ным или центростремительным ускорением (а„). Очевидно, что

а = аг + аn; а = (6)

Касательное ускорение изменяет только значение скорости, а центростремительное — только ее направление.

Если ускорение является величиной постоянной (а — const), то движение называется равнопеременным (при а > 0 — рав­ноускоренное движение, при о < 0 — равнозамедленное движе­ние). Таким образом, при поступательном движении твердого тела все его точки описывают совершенно одинаковые линии и имеют одинаковую скорость и одинаковое ускорение (в данный момент времени).

Равнопеременное прямолинейное движение

В этом случае а_n = О, а_t = а = const и мгновенное ускоре­ние равно среднему ускорению за любой промежуток времени. Получим выражение скорости и пути в зависимости от времени для этого движения. Учитывая, что а = (v — v_o)/t, получим:

v=v₀ + at (7)

где v₀ — начальная скорость, а v — скорость в момент времени t. Так как v = ds/dt, то dS = v • dt; тогда

S =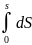 = = = v₀t + ;

S = v₀t + . (8)

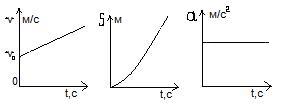
Рис. 5.

Подставляя выражение для t (t =(v-v₀)/a) полученное из

уравнения (6), в (7), получим:

s = v₀ + = (2v₀ + v - v0 ) = ,

откуда

- = 2aS

Если начальная скорость v₀ = 0, то получим следующие выражения:

v=at; S = ; = 2aS.

Согласно формулам (7) и (8), графики зависимостей v(t), S(t) и а(t) выглядят, как показано на рис. 5.

Для свободно падающего тела в безвоздушном пространстве а = g - 9.8 м/с²; тогда уравнения будут иметь вид

v = v₀ + gt; h = v₀t+ ; v2 - = 2gh.

Если v — const, то движение называется равномерным. В этом случае a = 0, и согласно формуле (7)

S = vt. (11)

Графики пути и скорости изображены на рис. 6.

Р авномерное движение материальной точки по окружности

Движение материальной точки по окружности происходит с постоянной по модулю скоростью — а_r = 0, а = а_n. Определим центростремительное ускорение (рис. 7).

Углы АОВ и BCD равны как углы со взаимно перпендику­лярными сторонами, v₁ = v₂ = v = const. Следовательно, АОВ и BCD подобны как равнобедренные с одинаковыми углами при вершине. Поэтому

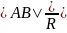= и .

Тогда согласно формуле (4), запишем

= a = = = .

При t, стремящемся к нулю, хорда АВ стремится к дуге S; поэтому

= = v; = = . (12)

Рисунок 7 позволяет еще раз убедиться, что полученное ускорение действительно является центростремительным, т.к. при При этом вектора v и а, имеющие оди­наковое направление, будут направлены вдоль радиуса окруж­ности к ее центру О. Наряду с линейной скоростью (v) рав­номерное движение материальной точки по окружности можно характеризовать угловой скоростью , но об этом поговорим в лекции №5.

Лекция N«2