Теорема Карно

В 1824 году французский физик Сади Карно рассмотрел ра­боту идеальной тепловой машины.

Карно показал, что идеальная тепловая машина, т.е. ма­шина, обладающая наибольшим коэффициентом полезного дей­ствия (к.п.д.), должна работать по циклу, состоящему из двух изотерм и двух адиабат. Пример такого цикла показан на рис. 3.

На участке 1-2 идеальный газ расширяется изотермически, т.е. все подводимое тепло идет на совершение работы А₁₂. На участке 2-3 газ расширяется адиабатически, т.е. работа A₂₃ совершается за счет внутренней энергии идеального газа. На участке 3-4 газ изотермически сжимается (А₃₄), отдавая тепло. На участке 4-1 идет адиабатическое сжатие газа (A₄₁), при этом его температура возрастает до первоначальной. Для идеальной тепловой машины имеет место теорема Карно:

Коэффициент полезного действия (к.п.д.) идеальной тепловой машины 𝛈* определяется соотношением

Здесь T₁ — температура нагревателя, T₂ — температура холо­дильника. Коэффициент полезного действия реальной тепловой машины 𝛈 всегда меньше, чем 𝛈*.

Покажем, что к.п.д. тепловой машины, работающей по ци­клу, изображенному на рис. 3, определяется формулой (1). Из определения к.п.д. имеем

При изотермическом расширении

При изотермическом сжатии

Следовательно,

и формула (1) имеет место, если ln(V₃/V₄) = ln(V₂/V₁) - Покажем это. Воспользуемся для адиабатического процесса уравнением Пуассона в виде TV^τ-1 = const, где τ —показатель адиабаты. Тогда очевидно, что

Отсюда имеем

Принимая во внимание (7) и (5), получим, что к.п.д. тепловой машины, работающей по циклу Карно, определяется формулой (1). Основные пути повышения к.п.д. реальной тепловой маши­ны могут быть таковы:

а) повысить разность температур между нагревателем и хо­лодильником,

б) уменьшить потери на трение при работе машины,

в) минимизировать потери тепла во внешнюю среду,

г) добиться более полного сгорания топлива.

Второе начало термодинамики допускает несколько эквива­лентных формулировок. Одна из них может быть сделана на основании теоремы Карно.

Невозможно осуществить такой круговой процесс, един­ственным следствием которого было бы полное превращение в работу теплоты, полученной от нагревателя (Ф1).

Двигатель, имеющий к.п.д. 100%, получил название вечного двигателя второго рода. Второе начало термодинамики утвер­ждает, что вечный двигатель второго рода невозможен (Ф 2).

Энтропия по Клаузиусу

Клаузиус в 1865 году ввел в рассмотрение новую термоди­намическую функцию 5, названную им энтропией. Изменение этой функции определяется с помощью соотношения

где dQ — количество теплоты, переданное телу при температу­ре T.

Изменение энтропии зависит от того, какие процессы проис­ходят с телом — обратимые или необратимые. Термодинами­ческий процесс называется обратимым, если при совершении его сначала в прямом, а затем в обратном направлении как сама система, так и все внешние тела, возвращаются в первоначаль­ное состояние. Если это не выполнено, то процесс называется необратимым. Не вдаваясь в детали доказательства, отметим, что для обратимости процесса необходимо и достаточно, чтобы на любой его стадии система находилась в состоянии термоди­намического равновесия.

Можно показать, что для обратимого цикла 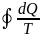= 0, а для необратимого < 0.

При переходе системы из начально­го состояния (1) в конечное состояние (2) изменение энтропии может быть найдено по формуле:

Второе начало термодинамики (ФЗ). Энтропия замкнутой си­стемы материальных тел есть неубывающая функция времени