Следствия из преобразований Лоренца

1. Относительность одновременности событий. Из пре­образований Лоренца вытекает, что если два независимых со­бытия происходят в системе К в один и тот же момент времени (t₁ = t₂)ив одном месте (х₁ = х₂), то в системе К' эти события также будут происходить в одной точке (х'₁ = х'₂) и одновремен­но (t'₁ = t'₂). В том случае, когда события в системе К разоб­щены (х₁ ≠ х₂), но одновременны (t₁ = t₂), в системе К' эти независимые события разобщены (х'₁ ≠ х'₂) и неодновременны (t'₁ ≠ t'₂).

2. Относительность длительности событий (промежутков времени). Пусть в системе К’ в одной точке х'₁ = х'₂ =a проис­ходит событие, длительность которого ∆τ = t'₁ = t'₂ . Согласно

преобразованию Лоренца (8) для времени в системе К это со­бытие будет длиться в течение промежутка времени

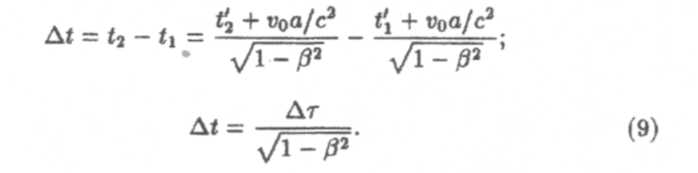
Из (9) вытекает, что длительность события, происходящего в некоторой точке, наименьшая в системе отсчета, относительно которой эта точка покоится. Собственное время ∆τ, отсчитан­ное по часам, неподвижным относительно тела, всегда меньше, чем время ∆t, отсчитанное по часам, движущимся относительно тела. В пределе малых скоростей (v « с) длительности событий ∆t ≈∆τ.

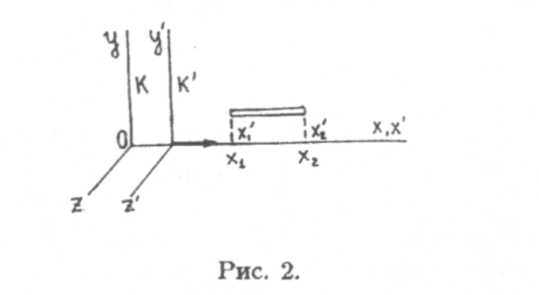
3. Относительность длины (размеров) тел. Рассмотрим стержень, расположенный вдоль оси х' и покоящийся относи­тельно системы К'. Клина его в системе К' равна l₀ = х'₂ - х'₁ (рис. 2).

В системе К скорость стержня v₀, координаты концов х₁ и х₂ надо отметить в один и тот же момент времени t₁ = t₂=t Длина стержня в системе К равна l= х₂ — х₁. Чтобы найти связь между l и l₀, используем преобразования (8):

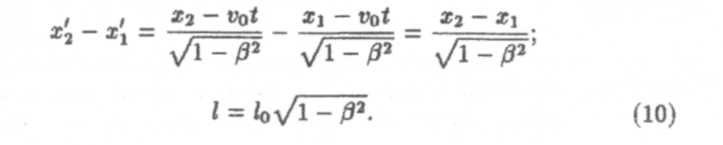
Линейные размеры тела наибольшие в той инерциальной систе­ме отсчета, относительно которой тело покоится (l₀ > l). При этом поперечные размеры тел одинаковы во всех инерциальных системах отсчета.

4. Релятивистский закон сложения скоростей. Скорости ма­териальной точки вдоль оси х (рис, 1, 2) в системах К и К' определяются как v_x = dx/dt и v'_x — dx'/dt'. Согласно преобра­зованиям Лоренца (8)

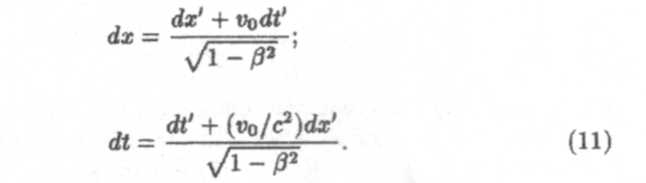
Разделив в (11) первое равенство на второе, получим реляти­вистский закон сложения скоростей:

Пусть скорость v'_x = с. Тогда

что является следствием постулата о постоянстве скорости све­та во всех системах отсчета. В приближении малых скоростей v « с имеем v_x = v'_x = v₀, т.е. классический закон сложения скоростей (2).

Основной закон релятивистской динамики для материальной точки

В конце 19 века на опытах с быстро движущимися электрона­ми было установлено, что масса тела зависит от его скорости, возрастая с увеличением скорости по закону

где m_o — масса покоя, измеренная в неподвижной относительно тела системе отсчета, am — релятивистская масса, измерен­ная в системе отсчета, движущейся со скоростью v. При v < с т = m_o = const. Основной закон динамики в релятивистской механике имеет вид:

где р — релятивистский импульс:

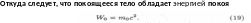
Уравнения (14) и (15) внешне совпадают с основным уравнением классической механики, если в качестве массы брать реляти­вистскую массу т (13), но (14-15) инвариантны по отношению к преобразованию Лоренца (8). В замкнутой системе реляти­вистский импульс системы сохраняется (р = const).