
- •Введение
- •Кинематика поступательного движения Введение
- •Кинематика поступательного движения. Основные кинематические характеристики
- •Скорость
- •Ускорение
- •Равнопеременное прямолинейное движение
- •Динамика поступательного движения Основные законы динамики
- •Первый закон Ньютона
- •Второй закон Ньютона
- •Третий закон Ньютона
- •Закон изменения импульса
- •Закон сохранения импульса
- •Реактивное движение
- •Разновидности сил, играющих важную роль в механических процессах Классификация фундаментальных взаимодействий, известных современной физике
- •Сила трения
- •Закон Гука
- •Сила тяготения
- •Центростремительная сила
- •Работа и энергия
- •Работа нескольких сил, приложенных к телу
- •Мощность
- •Энергия
- •Вращательное движение твердого тела
- •Момент инерции тела
- •Теорема Штейнера
- •Момент силы
- •Кинематические характеристики вращательного движения твердого тела
- •Основной закон динамики вращательного движения (аналог второго закона Ньютона)
- •Кинетическая энергия вращающегося тела
- •Момент импульса
- •Поступательным и вращательным движением
- •Закон изменения и сохранения момента импульса
- •Сумма моментов импульсов тел, составляющих замкнутую систему, есть величина постоянная.
- •Практические приложения закона сохранения момента импульса
- •Гармонические колебания
- •Уравнение гармонического колебания
- •Кинематические характеристики гармонического колебательного движения
- •Сложение гармонических колебаний
- •3. Сложение двух взаимно перпендикулярных гармонических колебаний
- •4. Частные случаи
- •Стоячие волны
- •Постулаты специальной теории относительности
- •Постулаты Эйнштейна
- •1. Принцип относительности.
- •Преобразования Лоренца
- •Следствия из преобразований Лоренца
- •Основной закон релятивистской динамики для материальной точки
- •Закон взаимосвязи массы и анергии
- •Молекулярная физика. Основные положения молекулярно-кинетической теории строения вещества
- •Вывод основного уравнения молекулярно кинетической теории идеального газа (уравнения Клаузиуса)
- •Уравнение Больцмана
- •Связь между давлением и температурой газа
- •Распределение молекул по скоростям и энергиям. Барометрическая формула
- •Число степеней свободы
- •Внутренняя энергия идеального газа
- •Первое начало термодинамики. Работа газа. Теплоемкость Основные понятия
- •Работа газа
- •Первое начало термодинамики
- •Теплоемкость газа
- •Адиабатический процесс
- •Второе начало термодинамики
- •Теорема Карно
- •Энтропия по Клаузиусу
- •Энтропия по Больцману
- •Явления переноса
- •Реальные газы Агрегатные состояния
- •Фазовые переходы
- •Эффект Джоуля-Томсона
- •Изотермы Ван-дер-Ваальса
- •Эффект Джоуля-Томсона для газа Ван-дер-Ваальса
- •Свойства жидкостей Поверхностное натяжение
- •Капиллярные явления
- •Свойства твердых тел Строение кристаллов
- •Кристаллизация, плавление и типы решеток
- •Тепловое расширение
- •Теплоемкость твердых тел
- •Основы гидродинамики Течение жидкости. Неразрывность струи
- •Уравнение Бернулли
- •Электростатика Электрические заряды. Закон Кулона
- •Закон сохранения электрического заряда
- •Закон Кулона
- •Напряженность электрического поля
- •Принцип суперпозиции полей
- •Силовые линии
- •Теорема Гаусса-Остроградского. Вычисление полей Поток вектора напряженности электрического поля
- •Теорема Гаусса-Остроградского
- •Напряженность поля равномерно заряженной бесконечной плоскости
- •Напряженность электрического поля между разноименно заряженными пластинами
- •Напряженность электрического поля равномерно заряженной тонкой нити бесконечной длины
- •Напряженность электрического поля равномерно заряженной сферы
- •Потенциал электрического поля. Потенциальная энергия взаимодействия зарядов
- •Работа точечного заряда по перемещению пробного заряда
- •Потенциальная энергия взаимодействия системы зарядов
- •Электрический потенциал
- •Связь между электрическим потенциалом и напряженностью электрического поля
- •Эквипотенциальные поверхности
- •Проводники в электрическом поле
- •1. Свойства проводников
- •2. Электрическая емкость
- •3. Энергия электростатического поля
- •Диэлектрики в электрическом поле
- •Постоянный электрический ток
- •1. Сила и плотность тока
- •2. Закон Ома
- •Электрические цепи
- •Закон Ома для полной цепи:
- •Контактные явления Работа выхода
- •Законы Вольта
- •Контактная разность потенциалов
- •Термоэлектрические явления
- •Электрический ток в полупроводниках
- •Собственная проводимость полупроводников
- •Примесная проводимость полупроводников
- •Контакт р- и п-полупроводников. Полупроводниковый диод
- •Магнитное поле токов
- •1. Магнитное поле и его характеристики
- •2. Закон Био-Савара-Лапласа
- •Напряженность поля в центре кругового витка
- •Напряженность поля прямолинейного проводника с током
- •Напряженность поля соленоида и тороида
- •Действие магнитного поля на проводник с током и движущийся заряд Закон Ампера
- •Сила Лоренца
- •Движение заряженной частицы в магнитном поле
- •Работа по перемещению
- •Магнитные свойства вещества
- •1. Парамагнетизм и диамагнетизм
- •Ферромагнетизм
- •Закон электромагнитной индукции Фарадея Энергия магнитного поля
- •Закон электромагнитной индукции Фарадея
- •Колебательный контур. Излучение электромагнитных волн
- •Уравнения Максвелла. Электромагнитные волны
- •Свет и его свойства. Геометрическая оптика Свойства света
- •Геометрическая оптика
- •Дисперсия света
- •Типы спектров
- •Основные фотометрические характеристики
- •Интерференция света Условия возникновения и сущность явления интерференции
- •Условия максимумов и минимумов интерференционной картины
- •Применение интерференции света.
- •Дифракция света Принцип Гюйгенса-Френеля. Зоны Френеля
- •Дифракция Френеля
- •Дифракция Фраунгофера
- •Поляризация света Естественный и поляризованный свет
- •Поляризация при двойном лучепреломлении
- •Вращение плоскости поляризации
- •Законы теплового излучения
- •Свойства теплового излучения
- •Характеристики теплового излучения
- •Поглощательные характеристики тела
- •Понятие абсолютно черного тела
- •Законы излучения абсолютно черного тела
- •Формула Планка
- •Квантовые свойства электромагнитного излучения. Внешний фотоэффект
- •Масса и энергия фотона Световое давление
- •Эффект Комптона
- •Строение атома водорода по Бору
- •Первый постулат Бора.
- •Второй постулат Бора.
- •Элементы квантовой механики. Частица в одномерной потенциальной яме Корпускулярно-волновой дуализм
- •Общее нерелятивистское уравнение Шредингера
- •Стационарное уравнение Шредингера
- •Строение ядра атома. Виды радиоактивного распада
- •Закон радиоактивного распада
- •Цепная реакция. Устройство и принцип действия ядерного реактора
- •Биологическое действие радиоактивных излучений Элементы дозиметрии радиоактивных излучений
- •Источники радиоактивных излучений
- •Действие облучения на органы и ткани
- •Механизм биологического действия радиации
- •Практическое использование ионизирующих излучений
- •Современные представления о строении элементарных частиц. Лептоны, кварки, глюоны. Кварки
- •Лептоны
- •Физический вакуум
- •Виртуальные частицы
- •Строение и эволюция Вселенной
- •Закон эволюции. Критическая плотность
Мощность
Для оценки эффективности механизма надо учесть, как быстро выполняет он работу. С этой целью вводится физическая величина — мощность.
Мощность равна отношению работы ко времени ее совершения:
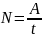
Измеряется мощность в ваттах: мощность механизма, совершающего работу в 1 Дж за 1 с


Если работа изменяется с течением времени, то

Энергия
Энергия — важнейшая величина, характеризующая состояние системы, способность системы совершать работу, переходя из одного состояния в другое.
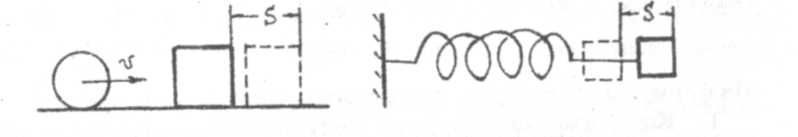
Рис.4 Рис.5
Например, катящийся шар, сталкиваясь с некоторым телом, переместит его и, следовательно, совершит работу. Значит, катящийся шар обладает энергией (рис. 4). Растянутая пружина, сокращаясь, будет перемещать свои витки (или другое тело) и, следовательно, совершит работу (рис. 5). Тело, приподнятое над землей на некоторую высоту, будучи освобожденным от связи, начинает падать, т.е. перемещаться и, следовательно, совершать работу. Значит оно обладает энергией (рис. 6).
Отметим, что шар, тело и пружина обладают энергией независимо от того, совершают они в данный момент работу или нет. Важно, что они обладают способностью совершать работу.
Обычно за конечное состояние системы принимают такое, в котором она уже не может совершать работу за счет данного вида энергии.
Из приведенных примеров видно, что если механическая энергия связана с движением системы или ее частей, то это кинетическая энергия {WK). Если энергия связана с взаимоположением тел или частей одного и того же тела, то это потенциальная энергия (Wn).
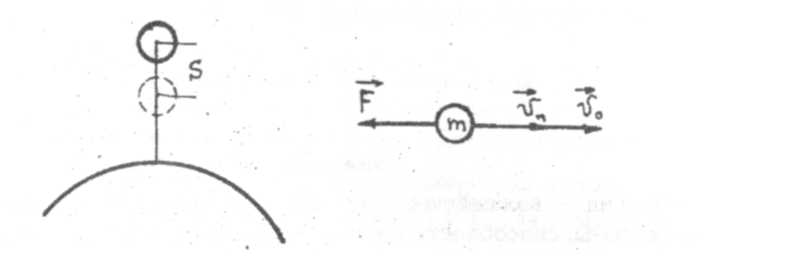
Рис. 6. Рис.7
Работа, совершаемая системой при переходе из одного состояния в другое, равна разности энергий системы в исходном (начальном) и конечном состояниях
A =Wo — Wn. (1)
Из формулы (1) следует, что энергия измеряется в джоулях.
1. Кинетическая энергия поступательно движущегося тела. Пусть под действием тормозящей силы F тело массой т замедлило на пути S свою скорость от оо До v„, имея ускорение о в течение промежутка времени t (рис. 7).
Тогда можно записать, что
 где
где


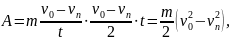
 .
(2)
.
(2)
Сопоставляя формулы (1) и (2), получим выражение кинетической энергии тела
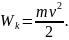 (3)
(3)
По формуле (3) определяется кинетическая энергия в классической механике, а релятивистское выражение для кинетической энергии определяется формулой (3а)
 (3a)
(3a)

Рис. 8. Рис.9.
где
то — масса тела, покоящегося относительно
наблюдателя (масса покоя); » — скорость
движения тела, значение которой
соизмеримо со скоростью света (с), с =
299793 км/с
 3-108
м/с.
3-108
м/с.
2. Потенциальная энергия упруго деформированного тела. Пусть упруго деформированный стержень растянулся (удлинился) на величину х при первоначальной длине х (рис. 8).
После устранения деформирующей силы сила упругости начнет укорачивать стержень. Пусть это укорочение совершилось от деформации х0 при силе упругости F0 до деформации хn, при силе Fn. Тогда работа силы упругости

По
закону Гука F
=
 .
Поэтому
.
Поэтому
 =
=
=k( )
и
)
и
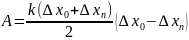 или
или
 (4)
(4)
После сравнения (4) и (1) получим выражение потенциальной энергии
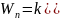 .
(5)
.
(5)
3. Потенциальная энергия тела в гравитационном поле.
Пусть тела массой М и т (рис. 9) взаимно притягиваются по закону всемирного тяготения так, что переместятся от расстояния г0 до г».
Разобьем перемещение на бесконечно малые отрезки dr и определим работу на одном таком отрезке:

Знак минус объясняется тем, что dA > 0 (система сама совершает работу), a dr < 0 (расстояние уменьшается).
Тогда вся работа
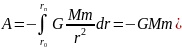

 .
(6)
.
(6)
Сравнивая равенство (6) с формулой (1), имеем выражение потенциальной энергии в поле тяготения
 .
(7)
.
(7)
При
г =
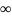 Wn
=
0 — это максимум, так как с уменьшением
г энергия Wa
будет
тоже уменьшаться.
Wn
=
0 — это максимум, так как с уменьшением
г энергия Wa
будет
тоже уменьшаться.
4. Потенциальная энергия тела, приподнятого над землей. Рассмотрим тело, приподнятое на небольшую высоту над землей h < R (рис. 10) (М — масса Земли, Я — ее радиус).
Согласно формуле (6),

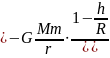
В "земных" задачах потенциальную энергию W„ = -GMmjR обычно принимают за начало отсчета, так как дальнейшее сближение тела т с Землей невозможно. Тогда
Wп = mgh. (8)
5. Закон сохранения и превращения энергии. В природе и технике повсеместно происходит превращение энергии из одних видов в другие: механической в электрическую (машинный генератор тока), электрической в световую (лампа накаливания) и т.п. Но опыт показывает, что полная энергия изолированной системы остается при этом постоянной
Wполн = const. (9)
Итак, энергия может переходить из одних видов в другие, но полная энергия изолированной системы остается постоянной — закон сохранения и превращения анергии.
При всех происходящих в природе процессах энергия не исчезает и не возникает вновь, а лишь передается от одних материальных объектов к другим, превращаясь из одной формы в другую в равных количествах.
В механике происходит превращение кинетической энергии в потенциальную, и наоборот. В силу своей всеобщности закон сохранения не выводится в общем виде, но может быть подтвержден любым конкретным процессом (см. рис. 11).
Рассмотрим, например, случай падения тела с некоторой высоты на землю. Запишем полную энергию тела в первом и втором состояниях (на высотах h1 и h2 соответственно).
W1=Wn1+Wk1=mgh1+0= mgh1 ,
W2=Wn2+Wk2=mgh2+ ,
v2=2g(h1-h2),
,
v2=2g(h1-h2),
W2=
mgh2
+
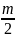 2g(h1-h2)=
mgh2+mgh1
- mgh2
=
mgh1.
2g(h1-h2)=
mgh2+mgh1
- mgh2
=
mgh1.
Видим, что W1 = W2 всегда, поскольку состояние (2) взято произвольно.
Закон сохранения и превращения энергии раскрывает физический смысл понятий энергии и работы. Рассматривая движение материи в широком смысле этого слова как всякий процесс, всякое изменение материи (а не только ее механическое перемещение), можно сказать, что энергия есть количественная и качественная характеристика различных форм движения материи, о работа — количественная характеристика превращения одних форм движения материи в другие.
Таким образом, работа и энергия — различные физические величины, хотя они выражаются в одинаковых единицах (джоулях): [A] = [W] = Дж.
Лекция №5
