Задание 6.7
В результате эксперимента получены данные, записанные в виде статистического ряда. Требуется:
а) найти размах варьирования и построить интервальный вариационный ряд;
б) построить полигон частот, гистограмму относительных частот;
в) вычислить эмпирическую функцию распределения и построить ее график;
г) найти числовые
характеристики выборки
,
Dв, σв, S2,
S;
д) считая выборку соответствующей нормальному распределению, найти доверительный интервал для математического ожидания при надежности γ = 0,95.
е) приняв в качестве нулевой гипотезу Н0: генеральная совокупность, из которой извлечена выборка, имеет нормальное распределение, – проверить ее, пользуясь критерием Пирсона при уровне значимости = 0,05.
114 |
92 |
66 |
98 |
58 |
100 |
76 |
82 |
54 |
68 |
74 |
98 |
102 |
52 |
110 |
84 |
118 |
86 |
92 |
60 |
62 |
86 |
116 |
82 |
70 |
94 |
66 |
90 |
98 |
74 |
94 |
68 |
108 |
78 |
120 |
98 |
50 |
100 |
62 |
106 |
76 |
82 |
60 |
102 |
74 |
110 |
94 |
86 |
70 |
84 |
70 |
92 |
54 |
90 |
82 |
68 |
100 |
58 |
102 |
78 |
84 |
118 |
86 |
62 |
76 |
116 |
108 |
74 |
52 |
86 |
58 |
84 |
66 |
82 |
48 |
78 |
106 |
90 |
66 |
102 |
90 |
50 |
108 |
100 |
74 |
60 |
82 |
120 |
84 |
92 |
76 |
106 |
68 |
94 |
70 |
98 |
114 |
78 |
110 |
62 |
Решение
а) Размах варьирования:
Rx = xmax – xmin = 120 – 48 = 72.
При k = 7 интервалах разбиения получаем шаг интервала:
h = Rx / k = 72 / 7 ≈ 10,3.
Результаты группировки сводим в таблицу.
i |
Границы интервала, [xi; xi+1) |
Частота, ni |
Накопление частот, Σnj |
Относительная частота, ni/n |
Накопление относительных частот, Σnj/n |
Середина интервала, zi |
1 |
48 – 58,3 |
10 |
10 |
0,1 |
0,1 |
53,15 |
2 |
58,3 – 68,6 |
15 |
25 |
0,15 |
0,25 |
63,45 |
3 |
68,6 – 78,9 |
17 |
42 |
0,17 |
0,42 |
73,75 |
4 |
78,9 – 89,2 |
16 |
58 |
0,16 |
0,58 |
84,05 |
5 |
89,2 – 99,5 |
17 |
75 |
0,17 |
0,75 |
94,35 |
6 |
99,5 – 109,8 |
14 |
89 |
0,14 |
0,89 |
104,65 |
7 |
109,8 – 120,1 |
11 |
100 |
0,11 |
1 |
114,95 |
Σ |
|
100 |
|
|
|
|
б) По полученной таблице строим полигон частот
и гистограмму относительных частот:
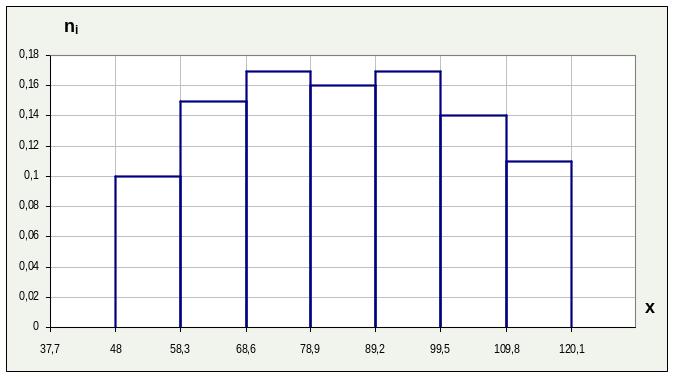
в) Используя значения накопленных частот, запишем эмпирическую функцию распределения:
F(x) = |
0 0,1, при 48,0 < x 58,3, 0,25, при 58,3 < x 68,6, 0,42, при 68,6 < x 78,9, 0,58, при 78,9 < x 89,2, 0,75, при 89,2 < x 99,5, 0,89, при 99,5 < x 109,8, 1, при х > 109,8. |
,
при x
48,0,и изобразим ее график:
г) Для определения числовых характеристик составим вспомогательную таблицу:
i |
ai |
bi |
zi |
ni |
nizi |
nizi2 |
1 |
48 |
58,3 |
53,15 |
10 |
531,5 |
28249,2 |
2 |
58,3 |
68,6 |
63,45 |
15 |
951,8 |
60388,5 |
3 |
68,6 |
78,9 |
73,75 |
17 |
1253,8 |
92464,1 |
4 |
78,9 |
89,2 |
84,05 |
16 |
1344,8 |
113030,4 |
5 |
89,2 |
99,5 |
94,35 |
17 |
1604,0 |
151332,7 |
6 |
99,5 |
109,8 |
104,65 |
14 |
1465,1 |
153322,7 |
7 |
109,8 |
120,1 |
114,95 |
11 |
1264,5 |
145348,5 |
Σ |
|
|
|
|
8415,3 |
744136,2 |
Выборочное среднее:
=
Σnizi
/ n = 8415,3 / 100 = 84,153;
выборочная дисперсия:
DВ =
2
= Σnizi
/ n – (
)2
= 744136,2 / 100 – 84,152
= 359,63;
выборочное среднее квадратическое отклонение:
=
=
= 18,96;
исправленная дисперсия:
S2 =
DВ
=
· 359,63 = 363,27;
исправленное среднее квадратическое отклонение:
S =
=
= 19,06.
д) По статистическим таблицам находим квантиль порядка (1 + γ) / 2 = 0,95 распределения Стьюдента с n – 1 = 99 степенями свободы zγ,n–1 = 1,9842.
Доверительный интервал для математического ожидания имеет вид ( –Δ; +Δ).
Предельная ошибка выборочного среднего:
Δ = zγ,n–1
·
/
=
1,9842 · 18,96 / 10 = 3,78.
Тогда интервал для математического ожидания a:
84,15 – 3,78 < a < 84,15 + 3,78;
80,37 < a < 87,93.
е) Проверим гипотезу о том, что данные получены из нормально распределенной генеральной совокупности с уровнем значимости = 0,05.
Для этого составим таблицу, в которой вычислим теоретические вероятности:
pi =
и теоретические частоты: m'i = npi.
i |
ai |
bi |
ni |
|
|
|
|
pi |
npi |
(ni – npi)2 npi |
1 |
-∞ |
58,3 |
10 |
-∞ |
-1,363 |
-0,500 |
-0,414 |
0,086 |
8,640 |
0,2141 |
2 |
58,3 |
68,6 |
15 |
-1,363 |
-0,820 |
-0,414 |
-0,294 |
0,120 |
11,967 |
0,7686 |
3 |
68,6 |
78,9 |
17 |
-0,820 |
-0,277 |
-0,294 |
-0,109 |
0,185 |
18,482 |
0,1188 |
4 |
78,9 |
89,2 |
16 |
-0,277 |
0,266 |
-0,109 |
0,105 |
0,214 |
21,404 |
1,3645 |
5 |
89,2 |
99,5 |
17 |
0,266 |
0,809 |
0,105 |
0,291 |
0,186 |
18,589 |
0,1358 |
6 |
99,5 |
109,8 |
14 |
0,809 |
1,352 |
0,291 |
0,412 |
0,121 |
12,106 |
0,2964 |
7 |
109,8 |
∞ |
11 |
1,352 |
∞ |
0,412 |
0,500 |
0,088 |
8,812 |
0,5431 |
|
|
|
100 |
|
|
|
|
1 |
100 |
3,4413 |
Наблюдаемое значение критерия Пирсона:
=
=
3,4413.
Так как число оцениваемых параметров h = 2 (математическое ожидание и дисперсия), то число степеней свободы равно k – h – 1 = 7 – 2 – 1 = 4.
По статистическим
таблицам находим квантиль порядка 1 –
= 0,95 распределения
Пирсона
с
4 степенями свободы:
2(4; 0,95) = 9,4877.
Поскольку < 2(4; 0,95), то гипотезу о нормальном распределении принимаем. Иными словами, эмпирические и теоретические частоты различаются не значимо.