Задача 2

Умова:

Розв’занти графічно задачу лінійного програмування

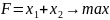
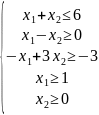
Розв’язання:

Запишемо обмеження у вигляді рівностей, замінивши знак нерівності на знак рівності, тоді кожна з умов є рівнянням прямої. Для побудови яких потрібно яких мати дві точки.

1.

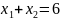
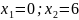
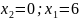
2.

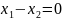
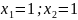
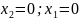
3.

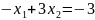
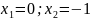
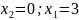
4.

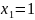
5.

Оскільки початкові обмеження є нерівності то геометричним місцем точок, що задовольняють дану нерівність є півплощина. Щоб визначити яку саме півплощина потрібно взяти довільну точку з півплощини і підставити її в конкретну нерівність. Якщо точка задовольняє дану нерівність, тоді беремо дану півплощину. В іншому випадку беремо іншу півплощину. Так ми одержимо область допустимих планів.

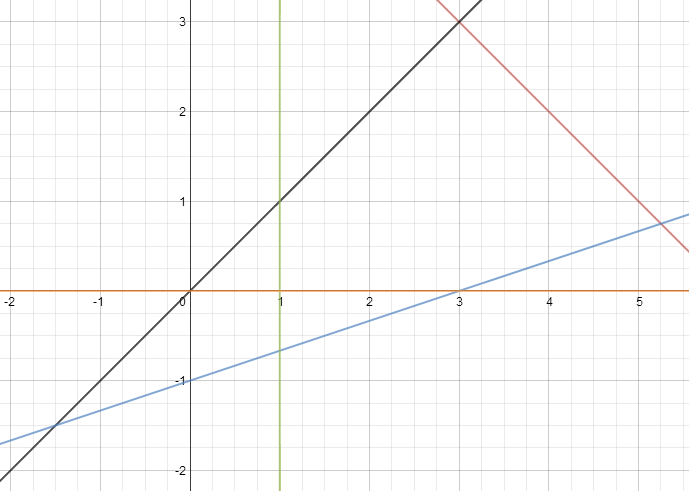
1

2

3

4

5

Будуємо нормаль - це вектор, який з’єднує початок координат зі точкою координат, якої є відповідні координати цільової функції.

Будуємо лінію рівня цільової функції і рухаємо її відносно нормалі. Остання точка в якій зупиниться цільова функція і буде точкою максимуму, яка знаходиться на перетині 2 прямих.

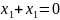
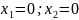
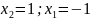
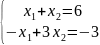
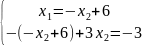
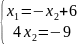
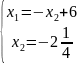
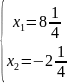
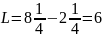
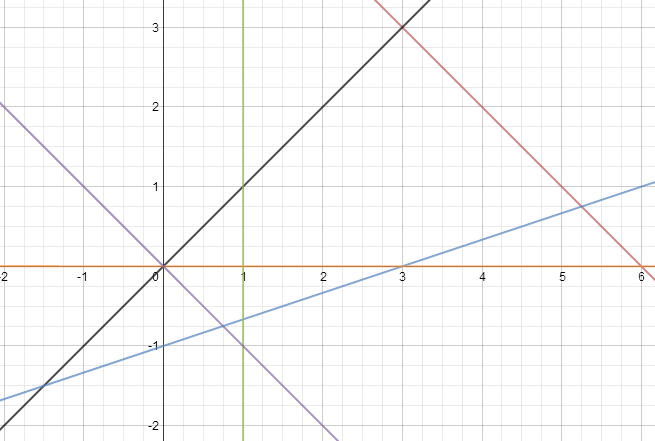
1

2

3

4

1

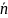
L

A

Задача 3

Умова:

Із гартівень A_i потрібно перевезти до магазинів B_j однорідний товар. Запаси товарів на гартівнях, потреби магазинів і вартості перевезень одиниці товару з кожної гуртівні до кожного магазину наведено в таблиці. Побудувати вихідний опорний план методом північно-західного кута, мінімальної вартості (мінімального елемента), методом подвійної переваги та апроксимації Фогеля. Знайти опорний план методом потенціалів, використовуючи один із вихідних опорних планів.

Магазини	B1	B2	B3	B4	Запаси
Гуртівні
A1	3	1	2	5	150
A2	2	5	1	4	160
A3	4	3	4	1	190
Потреби	90	110	220	110

Розв’язання:

Перевіримо необхідна і достатня умова розв'язання задачі.

∑A = 150 + 160 + 190 = 500

∑B = 90 + 110 + 220 + 110 = 530

Додаємо ще один стовбець гуртівні із запасами 30. Занесемо вихідні дані в розподільну таблицю.

Магазини	B1	B2	B3	B4	Запаси
Гуртівні
A1	3	1	2	5	150
A2	2	5	1	4	160
A3	4	3	4	1	190
A4	0	0	0	0	30
Потреби	90	110	220	110

Використовуючи метод північно-західного кута, побудуємо перший опорний план транспортної задачі.

Магазини	B1	B2	B3	B4	Запаси
Гуртівні
A1	3 [90]	1 [60]	2	5	150
A2	2	5 [50]	1 [110]	4	160
A3	4	3	4 [110]	1 [80]	190
A4	0	0	0	0 [30]	30
Потреби	90	110	220	110

У результаті отриманий перший опорний план, який є допустимим, оскільки всі вантажі з баз вивезені, потреба магазинів задоволена, а план відповідає системі обмежень транспортної задачі.

Підрахуємо число зайнятих клітин таблиці, їх 7, а має бути m + n - 1 = 7. Отже, опорний план є не виродженим. Значення цільової функції для цього опорного плану одно:

F(x) = 3*90 + 1*60 + 5*50 + 1*110 + 4*110 + 1*80 + 0*30 = 1210

Використовуючи метод найменшої вартості, побудуємо перший опорний план транспортної задачі.

Магазини	B1	B2	B3	B4	Запаси
Гуртівні
A1	3	1 [110]	2 [40]	5	150
A2	2	5	1 [160]	4	160
A3	4 [80]	3	4	1 [110]	190
A4	0 [10]	0	0 [20]	0	30
Потреби	90	110	220	110

У результаті отриманий перший опорний план, який є допустимим, оскільки всі вантажі з баз вивезені, потреба магазинів задоволена, а план відповідає системі обмежень транспортної задачі.

Підрахуємо число зайнятих клітин таблиці, їх 7, а має бути m + n - 1 = 7. Отже, опорний план є не виродженим. Значення цільової функції для цього опорного плану одно:

F(x) = 1*110 + 2*40 + 1*160 + 4*80 + 1*110 + 0*10 + 0*20 = 780

Використовуючи метод подвійної переваги, побудуємо перший опорний план транспортної задачі. У кожному рядку знаходимо мінімальний елемент. Ставимо навпроти нього знак V. Потім знаходимо мінімальний елемент кожного стовпця. Ставимо навпроти нього знак V. Шуканий елемент знаходиться в клітці (3;4) і дорівнює 1.

Магазини	B1	B2	B3	B4	Запаси
Гуртівні
A1	3	1[VV]	2	5	150
A2	2[V]	5	1[VV]	4	160
A3	4	3	4	1[VV]	190
A4	0	0	0	0[V]	30
Потреби	90	110	220	110

Шуканий елемент знаходиться в клітці (2;3) і дорівнює 1.

Магазини	B1	B2	B3	B4	Запаси
Гуртівні
A1	3	1[VV]	2	5	150
A2	2[V]	5	1[VV]	4	160
A3	4	3[V]	4	1	190
A4	0	0	0[V]	0	30
Потреби	90	110	220	110

Шуканий елемент знаходиться в клітці (1;2) і дорівнює 1.

Магазини	B1	B2	B3	B4	Запаси
Гуртівні
A1	3[V]	1[VV]	2[V]	5	150
A2	2	5	1	4	160
A3	4	3[V]	4	1	190
A4	0	0	0[V]	0	30
Потреби	90	110	220	110

Шуканий елемент знаходиться в клітці (1;3) і дорівнює 2.

Магазини	B1	B2	B3	B4	Запаси
Гуртівні
A1	3[V]	1	2[VV]	5	150
A2	2	5	1	4	160
A3	4	3	4[V]	1	190
A4	0	0	0[V]	0	30
Потреби	90	110	220	110

Шуканий елемент знаходиться в клітці (3;3) і дорівнює 4.

Магазини	B1	B2	B3	B4	Запаси
Гуртівні
A1	3	1	2	5	150
A2	2	5	1	4	160
A3	4[V]	3	4[VV]	1	190
A4	0	0	0[V]	0	30
Потреби	90	110	220	110

Шуканий елемент знаходиться в клітці (3;1) і дорівнює 4.

Магазини	B1	B2	B3	B4	Запаси
Гуртівні
A1	3	1	2	5	150
A2	2	5	1	4	160
A3	4[VV]	3	4	1	190
A4	0[V]	0	0	0	30
Потреби	90	110	220	110

Шуканий елемент знаходиться в клітці (4;1) і дорівнює 0.

Магазини	B1	B2	B3	B4	Запаси
Гуртівні
A1	3	1	2	5	150
A2	2	5	1	4	160
A3	4	3	4	1	190
A4	0[VV]	0	0	0	30
Потреби	90	110	220	110

Магазини	B1	B2	B3	B4	Запаси
Гуртівні
A1	3	1 [110]	2 [40]	5	150
A2	2	5	1 [160]	4	160
A3	4 [60]	3	4 [20]	1 [110]	190
A4	0 [30]	0	0	0	30
Потреби	90	110	220	110

У результаті отриманий перший опорний план, який є допустимим, оскільки всі вантажі з баз вивезені, потреба магазинів задоволена, а план відповідає системі обмежень транспортної задачі.

Підрахуємо число зайнятих клітин таблиці, їх 7, а має бути m + n - 1 = 7. Отже, опорний план є невиродженим. Значення цільової функції для цього опорного плану одно:

F(x) = 1*110 + 2*40 + 1*160 + 4*60 + 4*20 + 1*110 + 0*30 = 780

Використовуючи метод Фогеля, побудуємо перший опорний план транспортної задачі. Для кожного рядка і стовпця таблиці умов знайдемо різниці між двома мінімальними тарифами, записаними в даній ладі або стовпці, і помістимо їх у відповідному додатковому стовпці або рядку.

Магазини	B1	B2	B3	B4	Запаси
Гуртівні
A1	3	1 [110]	2 [40]	5	150
A2	2	5	1 [160]	4	160
A3	4 [60]	3	4 [20]	1 [110]	190
A4	0 [30]	0	0	0	30
Потреби	90	110	220	110

Зведемо всі обчислення в одну таблицю.

Магазини	B1	B2	B3	B4	Запаси	d1	d2	d3	d4	d5
Гуртівні
A1	3	1 [110]	2 [40]	5	150	1	1	1	1	-
A2	2	5	1 [160]	4	160	1	1	1	-	-
A3	4 [60]	3	4 [20]	1 [110]	190	2	1	0	0	0
A4	0 [30]	0	0	0	30	0	0	0	0	0
Потреби	90	110	220	110
d1	1	2	1	3
d2	1	2	1	-
d3	1	-	1	-
d4	1	-	2	-
d5	0	-	0	-

У результаті отриманий перший опорний план, який є допустимим, оскільки всі вантажі з баз вивезені, потреба магазинів задоволена, а план відповідає системі обмежень транспортної задачі.

Підрахуємо число зайнятих клітин таблиці, їх 7, а має бути m + n - 1 = 7. Отже, опорний план є невиродженим. Значення цільової функції для цього опорного плану одно:

F(x) = 1*110 + 2*40 + 1*160 + 4*60 + 4*20 + 1*110 + 0*30 = 780

Взявши за порний план метод північно-західного кута розв’язуєм задачу методом пренціалів.

Перевіримо оптимальність опорного плану. Знайдемо попередні потенціали u_i, v_i. по зайнятих клітинам таблиці, в яких u_i + v_i = c_ij, вважаючи, що u₁ = 0.

	v1=3	v2=1	v3=-3	v4=-6
u1=0	3 [90]	1 [60]	2	5
u2=4	2	5 [50]	1 [110]	4
u3=7	4	3	4 [110]	1 [80]
u4=6	0	0	0	0 [30]

Опорний план не є оптимальним, тому що існують оцінки вільних клітин, для яких u_i + v_i > c_ij. Вибираємо максимальну оцінку вільної клітини (4;1): 0. Для цього в перспективну клітку (4;1) поставимо знак «+», а в інших вершинах багатокутника чергуються знаки «-», «+», «-».

Магазини	B1	B2	B3	B4	Запаси
Гуртівні
A1	3 [-] [90]	1 [+] [60]	2	5	150
A2	2	5 [-] [50]	1 [+] [110]	4	160
A3	4	3	4[-] [110]	1 [+] [80]	190
A4	0 [+]	0	0	0 [-] [30]	30
Потреби	90	110	220	110

Цикл наведено в таблиці (4,1; 4,4; 3,4; 3,3; 2,3; 2,2; 1,2; 1,1; ). З вантажів х_ij стоять у мінусових клітинах, вибираємо найменше, тобто у = min (4, 4) = 30. Додаємо 30 до обсягів вантажів, що стоять у плюсових клітинах і віднімаємо 30 з Х_ij, стоять у мінусових клітинах. У результаті отримаємо новий опорний план.

\Магазини	B1	B2	B3	B4	Запаси
Гуртівні
A1	3 [60]	1 [90]	2	5	150
A2	2	5 [20]	1 [140]	4	160
A3	4	3	4 [80]	1 [110]	190
A4	0 [30]	0	0	0	30
Потреби	90	110	220	110

Перевіримо оптимальність опорного плану. Знайдемо попередні потенціали u_i, v_i. по зайнятих клітинам таблиці, в яких u_i + v_i = c_ij, вважаючи, що u₁ = 0.

	v1=3	v2=1	v3=-3	v4=-6
u1=0	3 [60]	1 [90]	2	5
u2=4	2	5 [20]	1 [140]	4
u3=7	4	3	4 [80]	1 [110]
u4=-3	0 [30]	0	0	0

Опорний план не є оптимальним, тому що існують оцінки вільних клітин, для яких u_i + v_i > c_ij. Вибираємо максимальну оцінку вільної клітини (3;1): 4. Для цього в перспективну клітку (3;1) поставимо знак «+», а в інших вершинах багатокутника чергуються знаки «-», «+», «-».

Магазини	B1	B2	B3	B4	Запаси
Гуртівні
A1	3 [-] [60]	1[+] [90]	2	5	150
A2	2	5 [-] [20]	1 [+] [140]	4	160
A3	4 [+]	3	4 [-] [80]	1 [110]	190
A4	0 [30]	0	0	0	30
Потреби	90	110	220	110

Цикл наведено в таблиці (3,1; 3,3; 2,3; 2,2; 1,2; 1,1; ). З вантажів х_ij стоять у мінусових клітинах, вибираємо найменше, тобто у = min (2, 2) = 20. Додаємо 20 до обсягів вантажів, що стоять у плюсових клітинах і віднімаємо 20 з Х_ij, стоять у мінусових клітинах. У результаті отримаємо новий опорний план.

Магазини	B1	B2	B3	B4	Запаси
Гуртівні
A1	3 [40]	1 [110]	2	5	150
A2	2	5	1 [160]	4	160
A3	4 [20]	3	4 [60]	1 [110]	190
A4	0 [30]	0	0	0	30
Потреби	90	110	220	110

Перевіримо оптимальність опорного плану. Знайдемо попередні потенціали u_i, v_i. по зайнятих клітинам таблиці, в яких u_i + v_i = c_ij, вважаючи, що u₁ = 0.

	v1=3	v2=1	v3=3	v4=0
u1=0	3 [40]	1 [110]	2	5
u2=-2	2	5	1 [160]	4
u3=1	4 [20]	3	4 [60]	1 [110]
u4=-3	0 [30]	0	0	0

Опорний план не є оптимальним, тому що існують оцінки вільних клітин, для яких u_i + v_i > c_ij. Вибираємо максимальну оцінку вільної клітини (1;3): 2. Для цього в перспективну клітку (1;3) поставимо знак «+», а в інших вершинах багатокутника чергуються знаки «-», «+», «-».

Магазини	B1	B2	B3	B4	Запаси
Гуртівні
A1	3 [-] [40]	1 [110]	2[+]	5	150
A2	2	5	1 [160]	4	160
A3	4 [+] [20]	3	4 [-] [60]	1 [110]	190
A4	0 [30]	0	0	0	30
Потреби	90	110	220	110

Цикл наведено в таблиці (1,3; 1,1; 3,1; 3,3; ). З вантажів х_ij стоять у мінусових клітинах, вибираємо найменше, тобто у = min (1, 1) = 40. Додаємо 40 до обсягів вантажів, що стоять у плюсових клітинах і віднімаємо 40 з Х_ij, стоять у мінусових клітинах. У результаті отримаємо новий опорний план.

Магазини	B1	B2	B3	B4	Запаси
Гуртівні
A1	3	1 [110]	2 [40]	5	150
A2	2	5	1 [160]	4	160
A3	4 [60]	3	4 [20]	1 [110]	190
A4	0 [30]	0	0	0	30
Потреби	90	110	220	110

Перевіримо оптимальність опорного плану. Знайдемо попередні потенціали u_i, v_i. по зайнятих клітинам таблиці, в яких u_i + v_i = c_ij, вважаючи, що u₁ = 0.

	v1=2	v2=1	v3=2	v4=-1
u1=0	3	1 [110]	2 [40]	5
u2=-1	2	5	1 [160]	4
u3=2	4 [60]	3	4 [20]	1 [110]
u4=-2	0 [30]	0	0	0

Опорний план є оптимальним, оскільки всі оцінки вільних клітин задовольняють умові u_i + v_i <= c_ij.

Мінімальні витрати складуть:

F(x) = 1*110 + 2*40 + 1*160 + 4*60 + 4*20 + 1*110 + 0*30 = 780.