Розділ 2. Практична частина Задача 1

Умова:

Для перевезення вантажу використовують машини типу A, B, C. Вантажопідйомність машини кожного типу відповідно дорівнює a, b, c. Потрібно перевести 270 тонн вантажу. За один рейс машина A витрачає d₁₁ кг і d₂₁ літрів, машина B – d₁₂ кг і d₂₂ літрів, машина C – d₁₃ кг і d₂₃ літрів мастильних матеріалів і бензину відповідно. На базі є d₁ кг мастильних матеріалів і d₂ літрів бензину. Витрати на експлуатацію машини A становить e₁ грошових одиниць, машини B – e₂ грошових одиниць, машини C – e₃ грошових одиниць. Скільки слід використати для перевезення вантажу машин типів A, B, C, щоб весь вантаж був перевезений і витрати на їх експлуатацію були мінімальні?

a=2, b=3, c=5, k=660;

d₁₁=1.5, d₁₂=2, d₁₃=1, d₁=385;

d₂₁=50, d₂₂=30, d₂₃=40, d₂=11000;

e₁=8, e₂=5, e₃=6.

Розв’язання:

Нехай машина типу A дорівнює x₁, B=x₂, C=x₃. Тоді можна записати що вантажопідйомність кожного типу автомобіля буде 2x₁, 3x₁, 5x₁ відповідно. Потрібно перевезти 660 тонн вантажу, це можно записати рівнянням

Кожна машина відповідного типу за рейс витрачає 1,5x₁, 2x₂ і 1x₃ мастильних матеріалів. На складі є 385 кг, які можуть використами машини при перевезенні вантажу. Це можна записати у вигляді рівняння:

Кожний тип машини використовує під час перевезення 50x₁, 30x₂ і 40x₃ літрів бензини. На складі є 11000 кг, які можуть використами машини при перевезенні вантажу. Це можна записати у вигляді рівняння:

На експлуатацію кожного виду машини витрачаються горошові одиниці 8x₁, 5x₂ і 6x₃ відповідно. Перевезення слід воконувати так, щоб витрати на експлуатацію цих машин були мінімальні. Це можна записати так:

Можна тепер скласти математичну модель транспортної задачі

Розв’яжемо задачу симплекс-методом.

Крок: 1

Позбудемося нерівностей в обмеженнях, ввівши в обмеження 2, 3 невід'ємні балансові змінні s₁, s_2. 

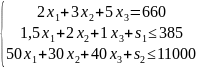
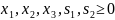
Крок: 2

Шукаємо в системі обмежень базисні змінні. З останньої системи обмежень можна виділити базисні змінні s_1, s₂. Не всі рівняння містять базисні змінні , це означає, що вихідна задача не містить в собі допустимого базисного розв'язку. Для його знаходження спочатку складемо і вирішимо допоміжну задачу. Таке рішення ще називають рішенням зі штучним базисом. Введемо в рівняння 1 штучну невід’ємну змінну r₁. Отримаємо наступну систему обмежень з базисними змінними r_1, s_1, s₂.

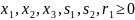
Метою розв'язку допоміжної задачі є отримання допустимого базисного рішення не містить штучних змінних (r₁)_. Для цього сформуємо допоміжну цільову функцію: G=r₁ і проведемо її мінімізацію в заданій системі обмежень. Якщо після мінімізації функції G її оптимальне значення буде дорівнює нулю і всі штучні змінні виявляться виведеними з базису, то отримане базисне рішення є допустиме базисне рішення вихідної задачі. Якщо ж після мінімізації функції G її оптимальне значення виявиться відмінним від нуля, значить вихідна система обмежень суперечлива (область допустимих рішень порожня) і вихідна завдання рішення не має. Для розв'язку допоміжної задачі симплекс-методом висловимо функцію G через вільні змінні, для цього: віднімемо з функції G рівняння 1. Функція G набуде вигляду: 

Тепер ми можемо сформувати початкову симплекс-таблицю. 

Крок: 3 

Початкова симплекс-таблиця 

БП	x1	x2	x3	s1	s2	r1	Рішення	Ставлення
r1	2	3	5	0	0	1	660	660 / 5 = 132
s1	3 2	2	1	1	0	0	385	385 / 1 = 385
s2	60	30	40	0	1	0	11000	11000 / 40 = 275
Q	8	5	6	0	0	0	0	-
G	-2	-3	-5	0	0	0	-660	-

Ітерація 0

БП	x1	x2	x3	s1	s2	Рішення	Ставлення
x3	2 5	3 5	1	0	0	132	-
s1	11 10	7 5	0	1	0	253	-
s2	44	6	0	0	1	5720	-
Q	28 5	7 5	0	0	0	-792	-
G	0	0	0	0	0	0	-

Отримано оптимальне рішення допоміжної задачі (знайдений мінімум функції G оскільки в рядку цільової функції немає негативних коефіцієнтів). Всі штучні змінні вийшли з базису і тому ми можемо приступити до вирішення вихідної задачі, прийнявши отримане базисне рішення в якості опорного. Рядок "G" нам більше не потрібна, прийняття рішення про спрямовуючий стовпці, у всіх наступних ітераціях, будемо приймати по рядку "Q".

Ітерація 1 

БП	x1	x2	x3	s1	s2	Рішення	Ставлення
x3	2 5	3 5	1	0	0	132	-
s1	11 10	7 5	0	1	0	253	-
s2	44	6	0	0	1	5720	-
Q	28 5	7 5	0	0	0	-792	-

Досягнуто оптимальне рішення, тому що в рядку цільової функції немає негативних коефіцієнтів. 

Відповіть:

Для перевезе вантажу з мінімальними витратами потрібно машин типу A=0, B=0 C=132. Сума мінімальних витрат буде становити 792 грошових одиниць.