Обґрунтування розрахунками параметрів конструкції екрану

Основною функцією екрану є послаблення поширення електромагнітногополя з одного просторового об’єму в інший об’єм. Крім суцільних металевих екранів широке застосування знаходять несуцільні металеві екрани, зокрема екрани із дротяних сіток для зменшення їх ваги та тиску вітру. В роботі розроблена математична модель екрану у вигляді сітки із тонких дротів колового перерізу (рис.3). На таку сітку зі сторони від’ємних Х (правий півпростір) падає плоска хвиля з амплітудою напруженості електричного поля та частотою коливань , причому вектор паралельний осям дротів. Відстань між осями дротів сітки позначимо через , а радіус дротів через . Ефект екранування можна пояснити так: під впливом падаючого поля в дротах виникнуть вторинні електричні струми. Ці струми створять вторинне випромінювання електромагнітного поля в правий та лівий півпростори.

Фаза коливань цього вторинного поля зсунута на 180⁰ в порівнянні з коливаннями падаючого поля. Падаюче поле проникає в лівий півпростір без зміни фази коливань. Тому в результаті інтерференції протифазних полів в лівому півпросторі падаюче поле буде значно послаблене або відсутнє у випадку суцільного екрану з ідеальною провідністю.

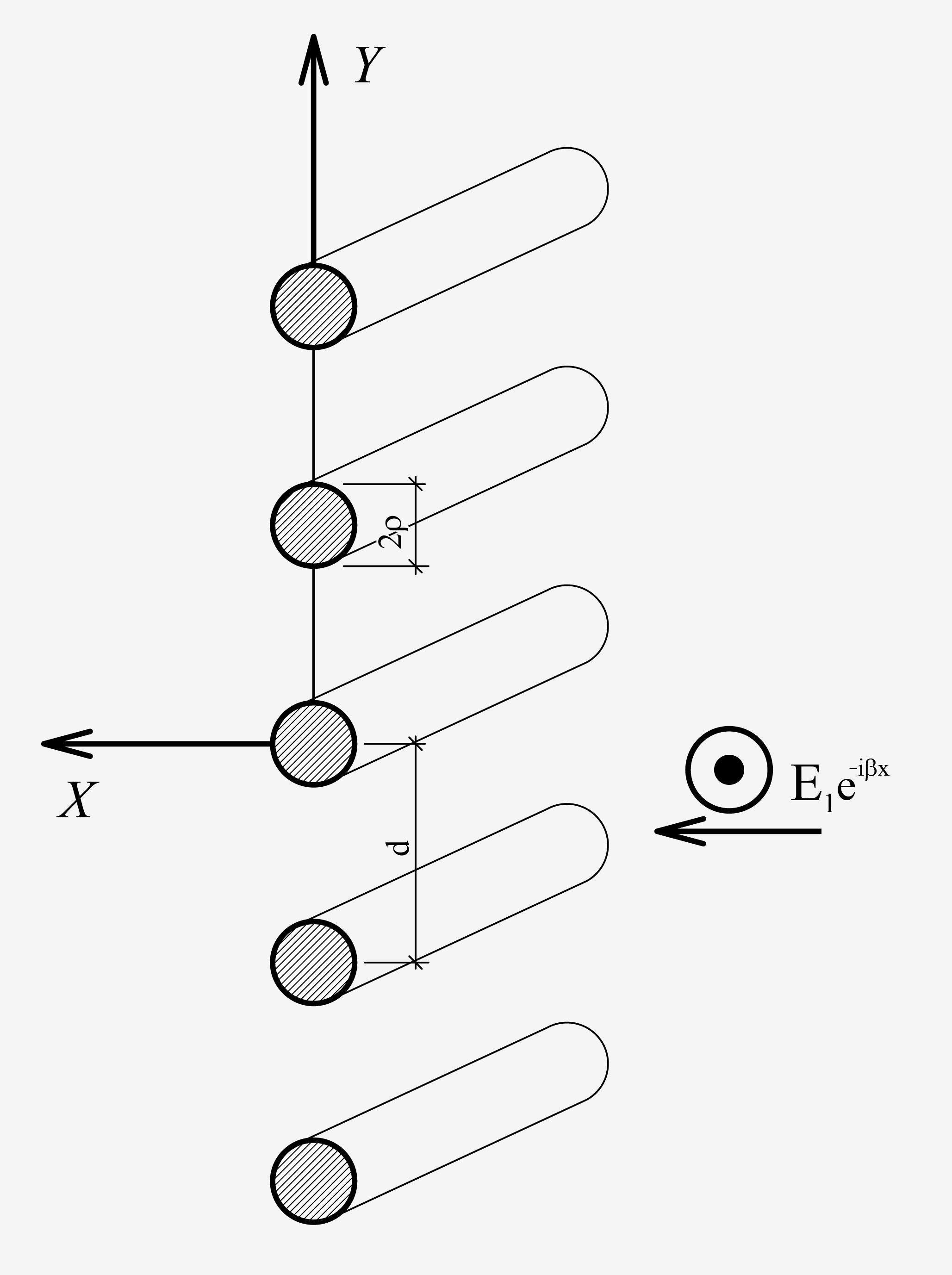
Рис. 3. Екран у вигляді сітки із тонких дротів колового перерізу.

В правому півпросторі накладання падаючого і відбитого полів з протилежними напрямками поширення та різницею фази їх коливань на величину 180⁰ приведе до утворення стоячої або змішаної хвилі. Властивості екранування згаданих електродинамічних систем описуються коефіцієнтом проходження хвилі ( ) та коефіцієнтом відбиття хвилі ( ). Згадані коефіцієнти можуть бути визначені для напруженості електричного поля , або для його потужності . Як відомо, потужність пропорційна квадрату напруженості , тобто . Коефіцієнтом проходження поля (за потужністю) називається відношення потужності поля, що пройшло в лівий півпростір до потужності падаючого поля . Коефіцієнтом відбиття поля (за потужністю) називається відношення потужності поля відбитої хвилі до потужності падаючого поля . Для розрахунку згаданих коефіцієнтів запропоновані наступні формули, отримані внаслідок розв’язку відповідної крайової електродинамічної задачі:

; , (1)

де - функції Ханкеля другого роду, нульового порядку; ; - довжина хвилі.

Для випадку “тонкої” сітки, коли виконується умова , коефіцієнти проходження та відбиття розраховуються за наступними наближеними формулами:

; , (2)

де: -циліндрична функція Неймана.

Для розрахунку відбивних властивостей густих ( ) дротяних сіток в роботі запропоновано наступні формули:

(3)

На основі математичних моделей (1-3) розроблена комп’ютерна програма “Екран” в середовищі комп’ютерної математики Matlab.

Комп’ютерна програма “Екран”

Розрахуємо параметри дротяної сітки для послаблення поля через екран на найвищій частоті спектру електромагнітного випромінювання сервера. В роботі [3] наведена величина такої частоти випромінювання f_max=2ГГц.

Наберемо в m - файлі Matlab наведену нижче програму, збережемо файл під назвою «ekran.m» (.m – розширення). Перевіримо роботу програми:

LAMDA =0.015:-0.005:0.001;

%LAMDA - довжина хвилі

kapa=2*pi./LAMDA;

%kapa- хвильове число

L1=20.0;

%L1=20.0 - максимальна довжина хвилі в [м]

L2=1.0;

%L2=1.0 - мінімальна довжина хвилі в [м]

r1=0.16;

r2=0.10;

r3=0.05;

%r1,r2,r3 - величини радіусів дротів однолінійної

%дротяної сітки в [м] для розрахунку екрануючих властивостей

%трьох варіантів її конструкції (відповідні варіанти

%позначені в змінних для розрахунку індексами 1,2,3).

d=0.5;

%d- відстань між осями дротів

DLD=d./LAMDA;

%відстань між осями дротів, нормована до довжини хвилі.

% в даному досліджені змінна DLD використовується в якості аргумента

% коефіцієнта проходження поля через екран

pd=pi*d;

brd=kapa.*d;

br1=kapa.*r1;

br2=kapa.*r2;

br3=kapa.*r3;

bj1=besselj(0,br1);

bj2=besselj(0,br2);

bj3=besselj(0,br3);

%bj - функція Бесселя

by1=bessely(0,br1);

by2=bessely(0,br2);

by3=bessely(0,br3);

%by= - функція Неймана;

bh1=besselh(0,2,br1);

bh2=besselh(0,2,br2);

bh3=besselh(0,2,br3);

%bh=bj+i*by - функція Ханкеля

yh1=besselh(0,2,br1);

yh2=besselh(0,2,br2);

yh3=besselh(0,2,br3);

N=200000;

% N – кількість повторень циклу

k=1;

y=0;

yy=0;

yh=0;

while k<=N

Z=brd*k;

hzJ=besselj(0,Z);

hzy=bessely(0,Z);

%hzh=hzJ-i*hzy;

y=y+besselj(0,Z);

yy=yy+bessely(0,Z);

yh=yh+besselh(0,2,Z);

k=k+1;

end;

Kp1=abs(1.0-LAMDA./(pd.*(yh1+2*yh))).^2;

%розрахунок коефіцієнта проходження за формулою 14.1

Kp2=abs(1.0-LAMDA./(pd.*(yh2+2*yh))).^2;

%розрахунок коефіцієнта проходження за формулою 14.3

Kp3=abs(1.0-LAMDA./(pd.*(yh3+2*yh))).^2;

%розрахунок коефіцієнта проходження за формулою 14.5

%Побудова трьох графіків

%subplot(1,5,[1 2 3 4]);

%plot(DLD,Kp1,DLD,Kp2,DLD,Kp3);

%subplot(1,5,5);

%axis('off');

%h1=text(-0.2,1,'Вихідні параметри:','FontName','Time New Roman Cyr','FontSize',12);

%h1=text(0.2,0.7,sprintf('L1=%g',L1),'FontSize',14);

%h1=text(0.2,0.6,sprintf('d=%g',d),'FontSize',14);

%Порівняння результатів розрахунків за формулами 14.1, 14.2 та 14.8.

%В якості еталону для порівняння прийняті результати Kp1, отримані

%за формулами Kp1 - формула 14.1; Кp4 - формула 14.2; Кp5 - формула 14.8.

Kp4=abs(1-1./(1-i*(pi*d./LAMDA).*(by1+2*yy))).^2;

Kp5=abs(1-1./(1+i*2*d./LAMDA*log(d./(2*pi*r1)))).^2;

subplot(1,5,[1 2 3 4]);

plot(DLD,Kp1,'g',DLD,Kp4,'b',DLD,Kp5,'r');

subplot(1,5,5);

axis('off');

h1=text(-0.2,1,'Вихідні параметри:','FontName','Time New Roman Cyr','FontSize',12);

h1=text(0.2,0.7,sprintf('L1=%g',L1),'FontSize',14);

h1=text(0.2,0.6,sprintf('d=%g',d),'FontSize',14);

h1=text(0.2,0.5,sprintf('r1=%g',r1),'FontSize',14);

На рисунку 4. наведено у вигляді графіків результати розрахунку коефіцієнта проходження поля від співвідношення для заданого діаметру дротів ρ.

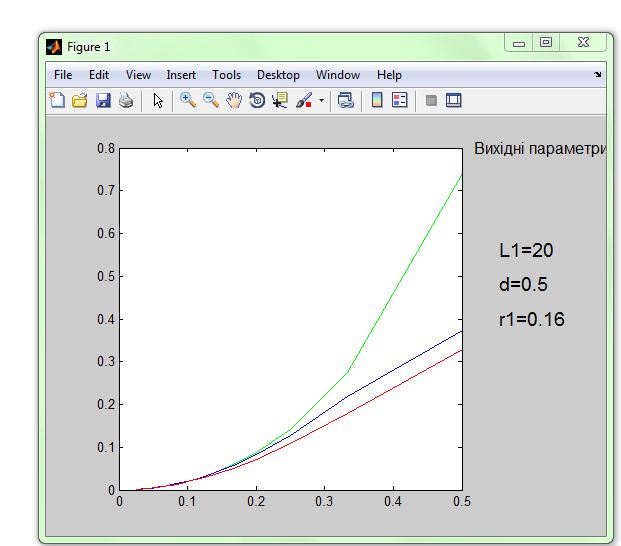
Рис. 4. Залежність величини коефіцієнта проходження поля від , розрахована за формулами 3.1 (зелений колір), 3.2 (синій колір) та 3.8 (червоний колір).

Користуючись графіком 4 вибираємо оптимальне значення радіуса дротяних елементів сітки, наприклад ρ= 0.1 мм та d = 0.2

Для заданого варіанту, наприклад, m=1, p=3 (див. перші оператори програми “pole”) розрахуйте та проаналізуйте розподіл напруженості електричної складової електромагнітного поля в екранованому серверному приміщенні (рис.5,6). Виявіть зони ризику несанкціонованого витоку інформації із серверного приміщення з використанням зонда у вигляді електричного диполя. Зони ризику витоку інформації розташовані в місцях максимальних значень концентрації електромагнітного поля.

Додаток 4