33. Измерение связей неколичественных переменных с использованием коэффициентов корреляции рангов Спирмена и Кендэлла; коэффициента взаимной сопряженности Пирсона.

Важной характеристикой совместного распределения двух случайных величин является ковариация (или корреляционный момент). Ковариация являетcя совместным центральным моментом второго порядка. Ковариация определяется как математическое ожидание произведения отклонений случайных величин:

,

где — математическое ожидание.

Свойства ковариации: Ковариация двух независимых случайных величин и равна нулю.

Абсолютная величина ковариации двух случайных величин и не превышает среднего геометрического их дисперсий: [9].

Ковариация имеет размерность, равную произведению размерности случайных величин, то есть величина ковариации зависит от единиц измерения независимых величин. Данная особенность ковариации затрудняет её использование в целях корреляционного анализа.

Для устранения недостатка ковариации был введён линейный коэффициент корреляции (или коэффициент корреляции Пирсона). Коэффициент корреляции рассчитывается по формуле:

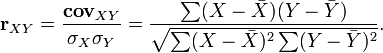
где , — среднее значение выборок.

Коэффициент корреляции изменяется в пределах от минус единицы до плюс единицы.

Линейный коэффициент корреляции связан с коэффициентом регрессии в виде следующей зависимости:

где — коэффициент регрессии, — среднеквадратическое отклонение соответствующего факторного признака.

Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая пара значений маркируется при помощи определенного символа. Такой график называется «диаграммой рассеяния».

Метод вычисления коэффициента корреляции зависит от вида шкалы, к которой относятся переменные. Так, для измерения переменных с интервальной и количественной шкалами необходимо использовать коэффициент корреляции Пирсона (корреляция моментов произведений). Если по меньшей мере одна из двух переменных имеет порядковую шкалу, либо не является нормально распределённой, необходимо использовать ранговую корреляцию Спирмена или (тау) Кендалла. В случае, когда одна из двух переменных является дихотомической, используется точечная двухрядная корреляция, а если обе переменные являются дихотомическими: четырёхполевая корреляция. Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, когда связь между ними линейна (однонаправлена).

Коэффициент ранговой корреляции Кендалла применяется для выявления взаимосвязи между качественными показателями, если их можно ранжировать. Значения показателя X выставляют в порядке возрастания и присваивают им ранги. Ранжируют значения показателя Y и рассчитывают коэффициент корреляции Кендалла:

,

где .

— суммарное число наблюдений, следующих за текущими наблюдениями с большим значением рангов Y.

— суммарное число наблюдений, следующих за текущими наблюдениями с меньшим значением рангов Y. (равные ранги не учитываются)

Если исследуемые данные повторяются (имеют одинаковые ранги), то в расчетах используется скорректированный коэффициент корреляции Кендалла:

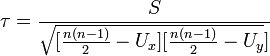
— число связанных рангов в ряду X и Y соответственно.

Коэффициент ранговой корреляции Спирмена. Каждому показателю X и Y присваивается ранг. На основе полученных рангов рассчитываются их разности и вычисляется коэффициент корреляции Спирмена: