2.3.2 Числовые показатели безотказности

Рассмотренные выше функции распределения достаточно объективно характеризуют безотказность. Однако для их получения требуется длительная и большая работа. Во многих практических задачах нет необходимости полностью характеризовать безотказность. Часто достаточно указать отдельные числовые параметры, которые компактным образом выражают наиболее существенные черты безотказности и проще в определении.

Такими показателями являются наработка на отказ и опасность отказа .

Наработкой на отказ называется среднее время безотказной работы линии. Определяется за достаточно длительный период наблюдений.

Рис. 2.16 Определение взаимосвязи  и R(t)

Допустим, ведется наблюдение за работой N одинаковых установок и фиксируется время работы до отказа каждого станка _рi где i= 1….N.

При решении практических задач надежности машин обычно случайные события (отказы) отождествляют со случайными величинами. Это позволяет наработку на отказ определять как математическое ожидание случайной величины:

(2.35),

где - время работы до отказа i-го станка.

При достаточно большом N имеем:

=

Выразим наработку на отказ через функцию надежности.

По результатам наблюдений можно построить график зависимости относительной частоты работающих станков от времени:

(2.36)

Рассматривается время наблюдения до момента отказа последнего станка (рис. 2.16). При достаточно большом N эта зависимость близка к функции надежности R(t).

Для пояснения этого перехода сделаем небольшое отступление. На практике вероятность случайного события определяется как относительная частота. При большом числе событий относительная частота события и его вероятность практически одно и тоже.

Например, из графика (рис.2.16) следует, что вероятность R(t_i) безотказной работы N=16 станков и относительная частота работоспособных установок на данный момент времени практически одинаковы и для нашего случая составляют:

Это означает, что после момента времени t_i продолжали работать 4 установки из 16. Это утверждение основано на следующем. Во-первых, замечено, что чем больше вероятность события, тем чаще оно происходит. Во-вторых, относительная частота события при многократном повторении испытаний обладает определенной устойчивостью значений, которая, как и вероятность события, отражает степень его объективной возможности. Например, относительная частота появления «n» годных деталей из общего числа N обработанных оказалась равной n/N =0,8. При повторении испытания с другими партиями этих деталей результат также близок к 0,8, так как условия обработки не изменились.

Далее время работы N станков t₀ разделим на j-интервалов одинаковой продолжительности t. Число интервалов должно быть равно количеству станков, т.е. j=1….N. В результате получаем распределение работающих станков n(t_j) по интервалам. Например, в первом интервале безотказно работали , так как за время t₁ произошло 3 отказа, на втором интервале так как за время t₂ произошло еще 3 отказа и так далее.

Очевидно, что будет представлять собой время безотказной работы станков на j-ом интервале. Теперь, согласно уравнению (2.29) можем записать:

(2.37)

Отношение есть относительная частота случайного события n(t_j), которая при достаточно большом N представляет собой вероятность безотказной работы станков на j-ом интервале времени наблюдения:

 R (t_j) (2.38)

Тогда получим:

 (2.39)

При N и это выражение принимает вид:

(2.40)

Таким образом, наработка на отказ для линии как системы машин соответствует площади под функцией надежности (рис. 2.14).

Из формулы (2.40) следует, что наработка на отказ должна быть каким-то образом связана с параметром функции надежности .

Ранее было сделано допущение, что поток отказов стационарный, т.е. на длительном периоде времени  = Const. На чем основано такое допущение?

Многочисленные наблюдения за работой оборудования показывают, что зависимость параметра  от времени работы имеет три характерных участка (рис.2.17).

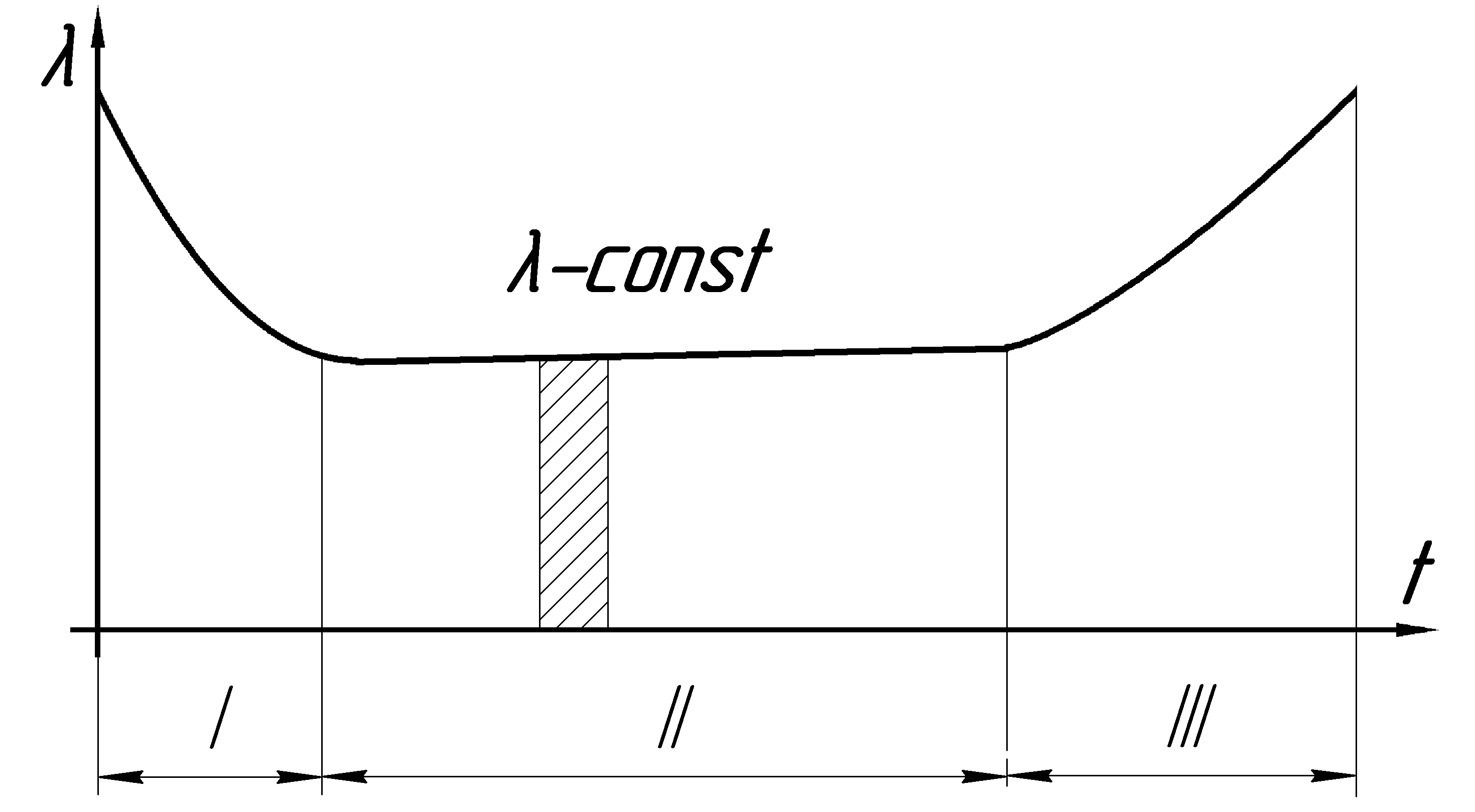
Рис. 2.17 Зависимость параметра 

от времени

На первом участке наблюдается повышенная частота появления отказов с интенсивным их сокращением (период приработки). Второй период - это период нормальной работы линии, который характеризуется наибольшей длительностью и наибольшей интенсивностью роста частоты появления отказов. Третий период – период катастрофического износа. Обычно в расчетах рассматривают период нормальной эксплуатации и принимают (t) = = Const. Тогда получаем очень важный для практики вывод:

(2.41)

Например, если  =0,0002 мин^-1, то _р=5000 мин, т.е. за межремонтный период среднее время работы линии между двумя очередными отказами составляет примерно 83 часа (примерно 2 недели при семичасовом режиме работы).

Опасность отказа. В реальных условиях эксплуатации линий параметр  в относительно короткие промежутки времени t принимает различные значения. Причем диапазон этих значений может быть достаточно велик. Поэтому для оценки надежности на небольшом интервале времени и для сравнения надежности в разных временных интервалах применяется второй числовой показатель безотказности, который называется опасностью отказа  (t).

Числовой показатель безотказности  (t) определяется на основе аксиомы условной вероятности. Согласно этой аксиоме вероятность события «А» при условии, что произойдет событие «В» равна вероятности событий «А» и «В», деленной на вероятность события «В»:

Р(А/В)= Р(АВ)/Р(В) (2.42)

Данная аксиома находит применение, когда решается следующая задача надежности. Линия проработала безотказно время t. Какова вероятность, что отказа на интервале t при дальнейшей работе.

Для решения этой задачи период времени t+ t через t₁. Тогда событием А будет вероятность безотказной работы линии в интервале времени «t- t₁» , событием В – вероятность безотказной работы в период от нуля до t. Событием «А-В» будет вероятность безотказной работы на интервале «0-t₁». Для данной задачи аксиома условной вероятности примет вид:

Рис. 2.18 Определение параметра  (t)

R(t,t₁) = (2.43)

Учитывая, что

F(t, t + t) = 1- R(t, t+t)= 1- R(t, t₁) (2.44)

получим

F(t, t + t)= 1 - = (2.45)

Из уравнения (2.46) следует, что опасность отказа как числовой показатель представляет собой плотность условной вероятности, т.е. отношение величины изменения значений функции надежности за короткий интервал времени t= t₁ – t к значению этой функции на время t (рис. 2.19):

= (2.46)

Эта локальная характеристика надежности на практике определяется следующим образом . Воспользуемся результатами наблюдения за работой N станков, которые представлены на рисунке 2.17 в виде графиков =f (t) и R(t). Возьмем фрагмент этих графиков в интервале j=5 равным t =t₁ – t (рис.2.19), из которого следует, что R(t) = и R(t +t) = . Тогда

= (2.47)

Рис. 2.19 Статистическая оценка 

где n(t) - число работающих станков на интервале времени t;

n(t +t) – число работающих станков на интервале t₁;

n – число отказов за интервал времени t.

Таким образом, определяется как отношение интенсивности отказов на коротком интервале времени к числу безотказно работающих станков в начале этого интервала. Допустим t = 1 час, тогда в нашем случае n = 2, n(t) = 8 и =28*1= 0,25 час^-1.

Обратимся к другому примеру, который носит сравнительный характер. Допустим, при t= 0 начали работать N станков. В течение 1 часа работы вышли из строя 50 станков. Проходит 30 часов работы. Работают 50 станков. Через час вышли из строя 5 станков. На каком интервале времени t₁ или t₂ надежность выше.

По условию задачи: при t = 0 число станков N= 1000

t = 1час n= 50 станков, n(t₁) =1000 станков

тогда  (t₁)= = 0,05 час^-1

при t₂ = 30 час и n(t₂) = 50 станков

тогда  (t₂)= = 0,10 час^-1

Ответ: надежность выше на первом интервале, так как на этом интервале опасность отказа меньше.