Закон равной вероятности

Если рассевание размеров зависит от переменных систематических погрешностей (например, от износа инструмента), то распределение их подчиняется закону равной вероятности.

При установившемся износе режущего инструмента распределение размеров вала увеличивается, а отверстия – уменьшается. Если непрерывная случайная величина принимает все значения интервала с одинаковой плотностью вероятности, то это распределение графически будет выражаться в виде прямоугольника с основанием и высотой . Распределение размеров при равномерном износе во времени подчиняется прямолинейному закону

.

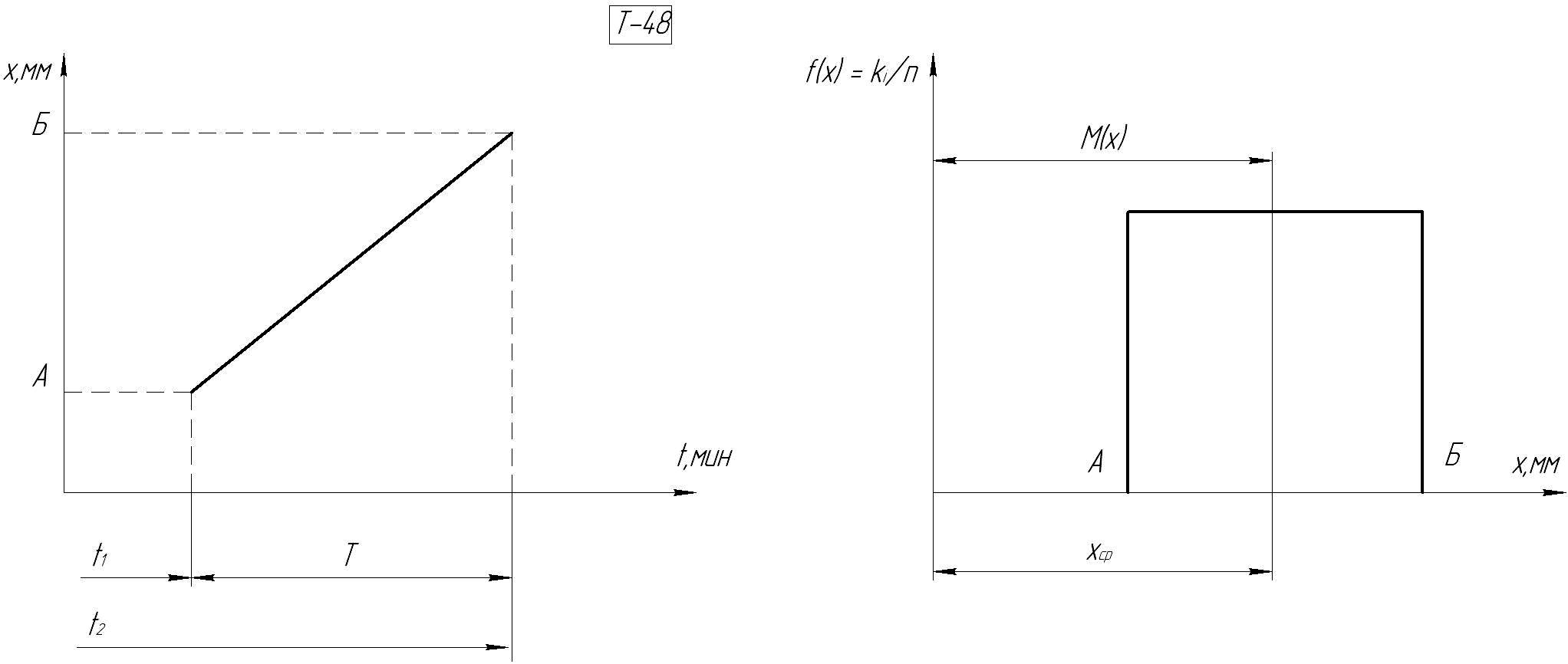
Рис. 45.2. Графическое изображение закона прямолинейного закона

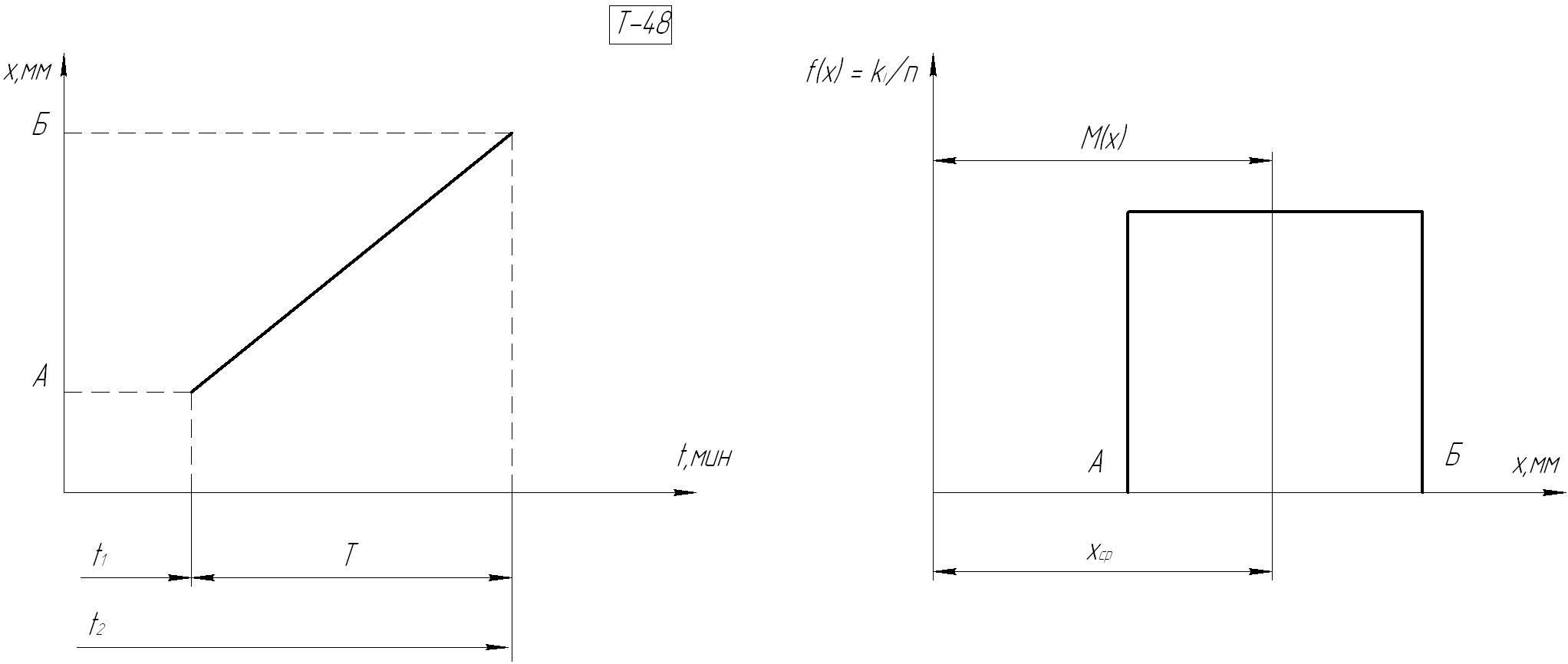
Рис. 45.3. Графическое изображение закона равной вероятности

.

Площадь прямоугольника равна единице. Это означает 100% вероятность появления размера в интервале от A до Б. .

Закон эксцентриситета (закон Релея)

Отражает распределение величин, характеризующимися их абсолютными значениями (т.е. без учёта знака). К этим величинам относятся: эксцентриситет, биение, разностенность, отклонение от параллельности, отклонение от перпендикулярности.

Формирование эксцентриситета втулки при двухмерном гауссовском распределении двух случайных величин x и y с параметрами: ; .

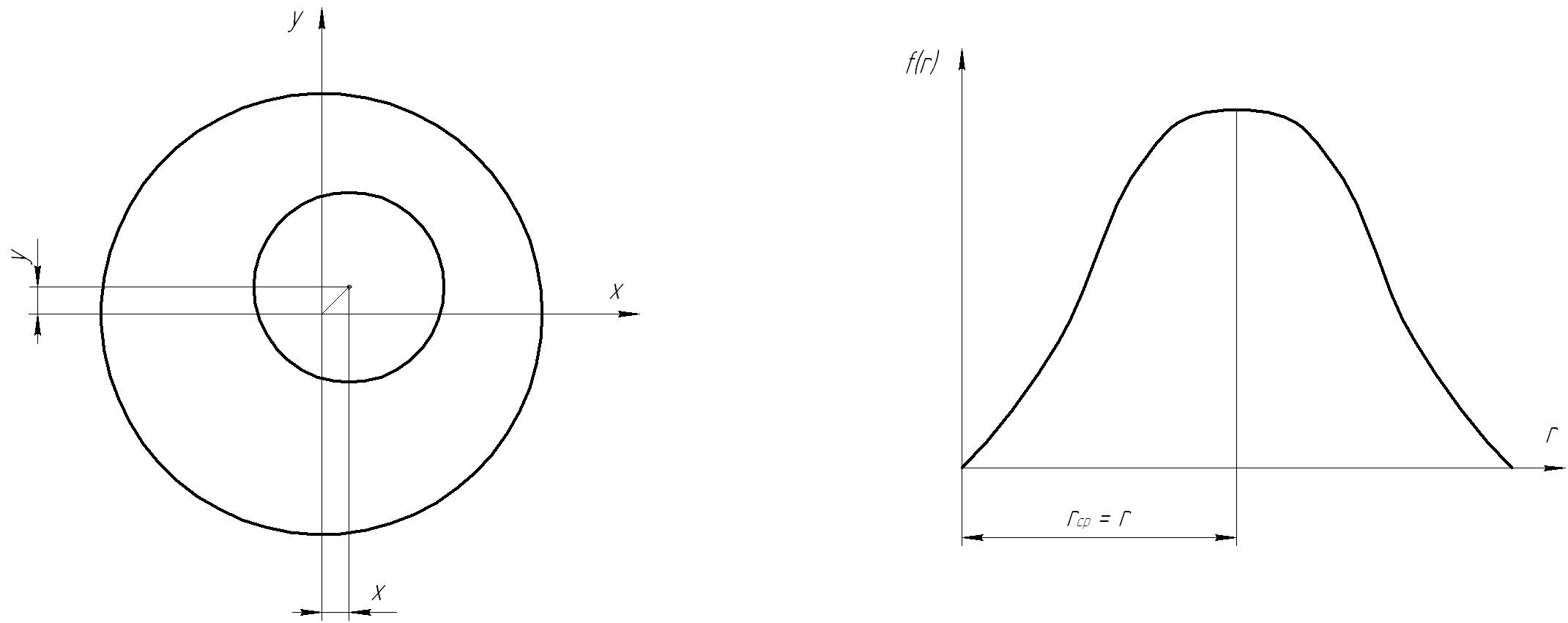
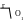
Рис. 45.4. Схема для определения параметров эксцентриситета

Рис. 45.5. Графическое изображение закона Релея

Закон распределения Релея однопараметрический:

.

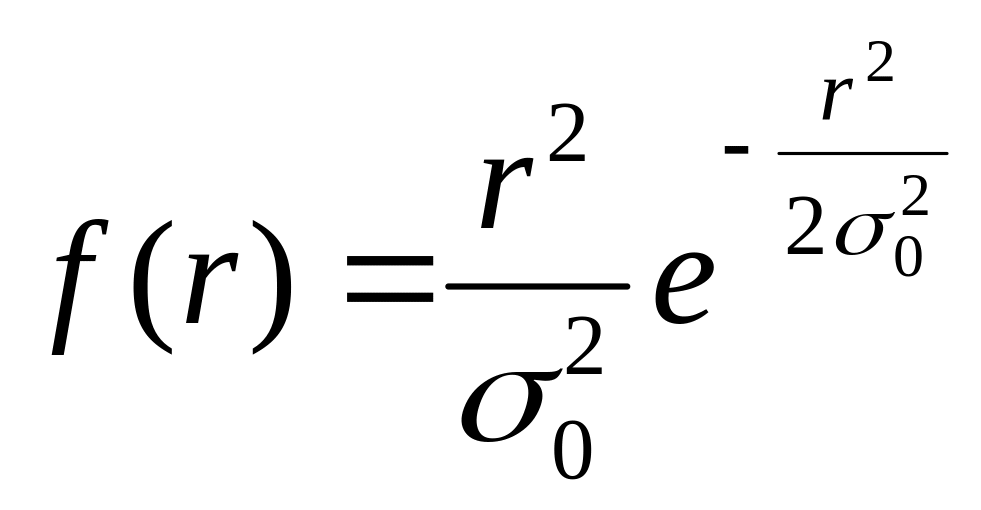Интегральный закон распределения эксцентриситета имеет вид:

,

.

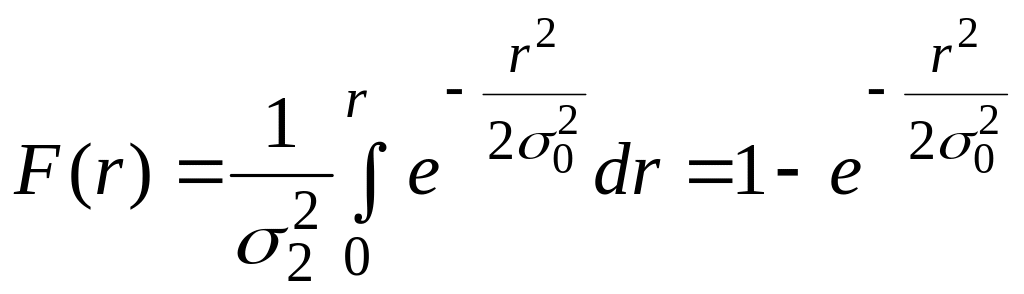Закон распределения модуля разности

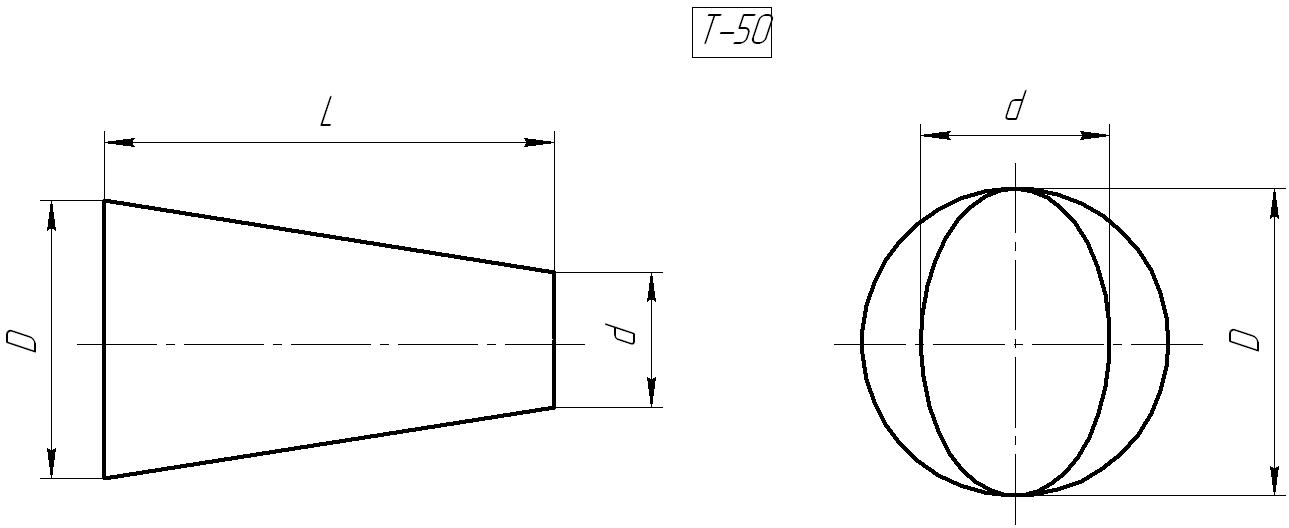
а) б)

Рис. 45.6. примеры отклонений расположения формы: а) конусообразность, б) овальность

Отклонение расположения и формы определяется абсолютными значениями разности 2 значений (овальность, конусообразность).

Если две случайные величины и имеют нормальное распределение с параметрами и и , то модуль разности этих величин имеет распределение, которое называется распределением модуля разности.

,

.

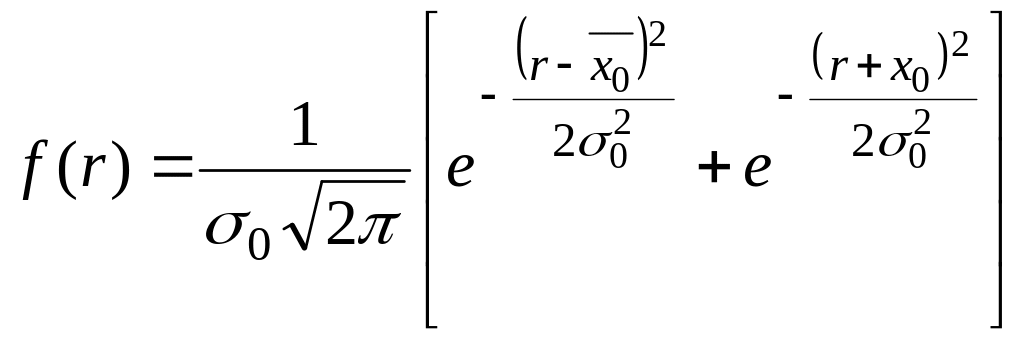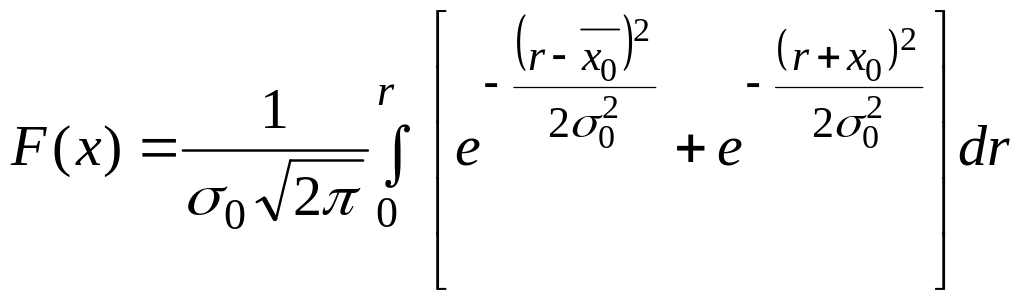Заменяем в последнем уравнении:

.

ρ₀=0

ρ₀=3

ρ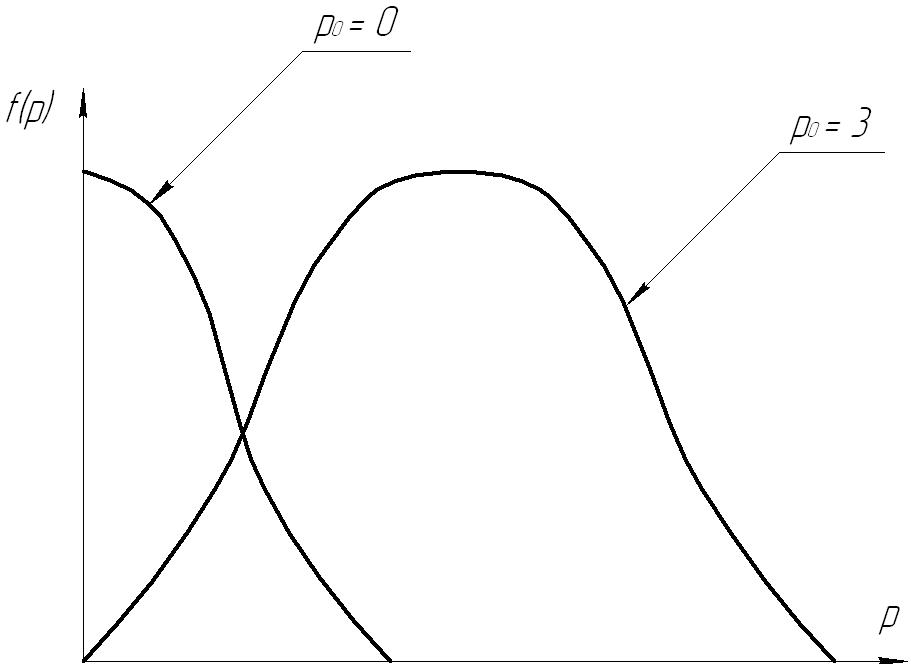

Рис. 45.7. Графическое изображение закона модуля разности

46. Композиция законов распределения

Если два независимых случайных слагаемых и имеют плотность распределения и и их сумма , то плотность распределения суммы:

.

Практический смысл композиции законов распределения заключается в суммировании погрешностей.

Систематические погрешности складываются алгебраически. Систематические погрешности со случайной складываются арифметически. Например, удлинение резца в результате нагрева может быть компенсировано его износом.

Рассеивание размеров в каждый момент времени определяется факторами независящими от нагрузки (зазором или натягом в подшипниках шпинделя, неравномерностью снимаемого припуска и др.), но оказывающими влияние на силовую нагруженность технологической системы.

Каждый из таких факторов проявляет своё действие независимо друг от друга, формируя суммарное поле рассеяния.

Поэтому общее поле рассеяния размеров в партии деталей, обрабатываемых на станке по методу автоматического получения, выражается формулой:

Здесь 1,2 - коэффициент, соответствующий распределению Симпсона, который используется для того, чтобы учесть возможные на практике отступления распределений отдельных составляющих от закона Гаусса, а также для некоторой «гарантии точности», поля рассеяния, обусловленные соответственно w_м - мгновенным расстоянием; w_б - погрешностью базирования; w_з - закрепления; w_пр - погрешностью приспособления; w_рег - погрешностью регулирования; w_изм - изменения и w_см - смещения уровня настройки.

Численные значения величин определяются для конкретных условий выполнения операций по фактическим значениям полей рассеяния или приближенным по справочникам.

Величина поля рассеяния вида обработки w_м составляет:

0,016…0,039 мм - для средних револьверных станков;

0,013…0,036 мм - для токарных;

0,004…0,017 мм - для круглошлифовальных.

Величина погрешностей базирования w_б и смещения w_см определяется конкретными расчетами в зависимости от формы опорных поверхностей и простановки размеров, а также от величины σ для данного случая.

Поле рассеяния, связанное с закреплением w_з в среднем составляет:

0,05…0,2 мм - в тисках;

0,01…0,2 мм - прихватами;

0,04…0,1 мм - в патроне;

0,02…0,1 мм - в зажимной гильзе.

Погрешность приспособлений w_пр = 0,005…0,02мм

Рассеяние, связанное с погрешностью регулирования w_рег составляет: 0,01…0,06мм - при установке по лимбу или индикатору 0,04…0,10мм - по жесткому упору (при особо тщательном регулировании w_рег = 0,02мм); 0,005…0,025 мм - по индикаторному упору; 0,10…0,13мм - по эталонной детали.

Поле рассеяния, характеризующее погрешность измерения пробных заготовок w_изм составляет: 0,045мм - при измерении штангенциркулем с ценой деления 0,02мм; 0,09мм - при измерении штангенциркулем с ценой деления 0,05мм.

При измерении микрометром w_изм = 0,006…0,014мм.

Общая погрешность обработки включает в себя все поля рассеяния размеров заготовок под влиянием причин случайного характера, а также систематические погрешности обработки Δ_обр= w + +Δ_сист

Величина Δ_сист представляет собой алгебраическую сумму неустранимых при постройке станка систематических погрешностей, возникающих при обработке заготовок и влияющих на их размеры.

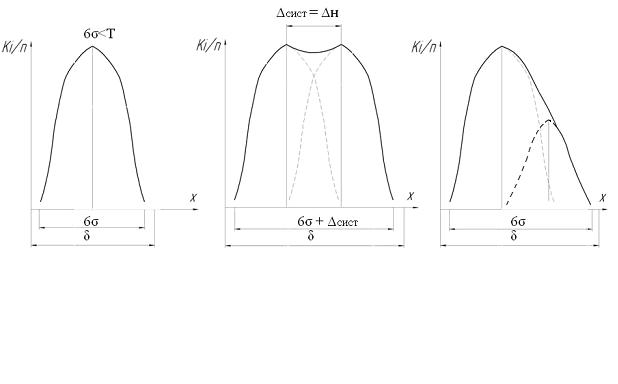
а) б) в)

Рис. 45.8. Графическое изображение формирования композиции законов распределения: а) кривая рассеяния размеров отверстий при развертывании первой разверткой, б) кривая рассеяния размеров отверстий при развертывании второй разверткой, в) кривая суммарного рассеяния размеров отверстий

Систематические погрешности не изменяют форму кривой рассеяния размеров, а только сдвигают положения ее вершины, соответственно, увеличивая общее поле колебания размеров партии обработанных заготовок, а, следовательно, и общую погрешность обработки.

Например, при развертывании партии заготовок рассеяние размеров подчиняется закону нормального распределения с полем рассеяния 6σ.

При смене развертки характер рассеяния не меняется, однако вершина кривой рассеяния смещается на величину разности диаметров старой и новой разверток.

Поле суммарного рассеяния размеров, обработанных обеими развертками, расширяется на величину этой разницы.

Когда измеряется вся партия заготовок, обработанная с нескольких настроек, то форма общей кривой рассеяния искажается и отличается от формы кривой Гаусса.

Кривая может иметь несколько вершин разной высоты соответственно числу настроек и количеству заготовок, обработанных с каждой настройки. Для уменьшения погрешностей настройки Δ_н=w_н необходимо сократить погрешность измерения w_изм пробных заготовок путем применения более точного измерительного инструмента и погрешность w_рег за счет использования более точных установочных устройств и усовершенствования конструкции механизмов перемещения и отсчетных лимбов станков.