4. Явление биений

При частоте возмущающей силы, близкой к частоте свободных колебаний точки, наступает явление, называемое биениями. Полагая в уравнении (2.41) x₀=0 и , рассмотрим колебания материальной точки, вызываемые лишь действием возмущающей силы:

Принимая , приведем это уравнение к виду:

Воспользуемся формулой:

Учтем, что , тогда:

(2.45)

Для исходных данных:

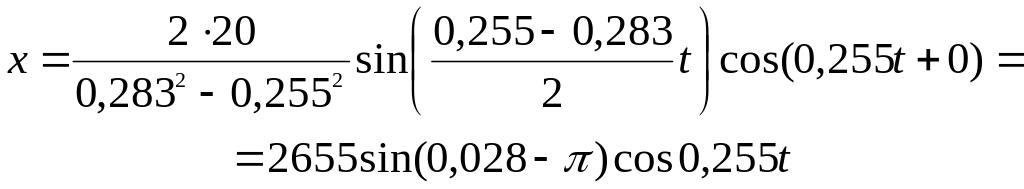(2.46)

Уравнение (2.45) определяет движение точки, являющееся результатом наложения дополнительных колебаний, вызванных действием возмущающей силы, на собственно вынужденные колебания в случае .

Введем обозначение:

Тогда уравнение (2.45) можно представить в виде:

(2.47)

Движение, определяемое уравнением (2.47), можно рассматривать как колебания частоты р и периода , амплитуда которых A(t) является периодической функцией.

Период изменения амплитуды:

(2.48)

Для исходных данных Т_А = 444,288.

График движения, определяемого уравнением (2.46) и называемого биениями, показан на рис. 2.11.

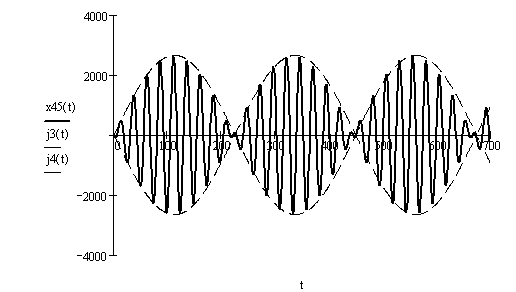
Рисунок 2.11 – График вынужденных колебаний при

2.5 Случай резонанса

Явление резонанса возникает при совпадении частот вынужденных и свободных колебаний точки, т.е. при р = к. В этом случае амплитуда вынужденных колебаний точки равна бесконечности. Дифференциальное уравнение вынужденных колебаний при р = к принимает вид:

(2.49)

Общее решение уравнения (2.49) будем искать в виде:

где х₁ – общее решение линейного однородного уравнения ;

х₂ – частное решение данного уравнения.

Однородное уравнение имеет решение:

Частное решение будем искать в виде:

Определим вторую производную по времени от последнего выражения:

Аналогично:

Подставив значения х₂ и в уравнение (2.49), определим В:

или:

Приравняв коэффициенты при синусе в обеих частях уравнения, получим:

Тогда общее решение дифференциального уравнения примет вид:

,

или

(2.50)

Второе слагаемое уравнения (2.50) представляет собой вынужденные колебания при резонансе. Для исходных данных оно будет иметь вид:

(2.51)

График вынужденных колебаний при резонансе показан на рис. 2.12.

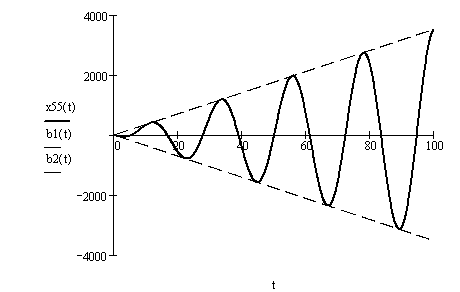
Рисунок 1.12 – График вынужденных колебаний при резонансе

2.6 Коэффициент динамичности при отсутствии и наличии сил сопротивления движению

Коэффициентом динамичности К_д называется отношение амплитуды вынужденных колебаний А_В к величине статического отклонения А₀:

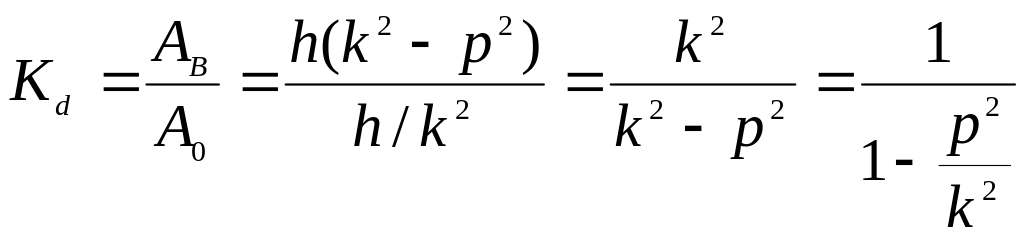(2.52)

Изменение амплитуды вынужденных колебаний А_В в зависимости от изменения частоты возмущающей силы р характеризуется графиком коэффициента динамичности – рисунок 2.13. На горизонтальной оси этого графика отложены значения отношения р/к, а на вертикальной оси – соответствующие значения , определенные по формуле (2.52).

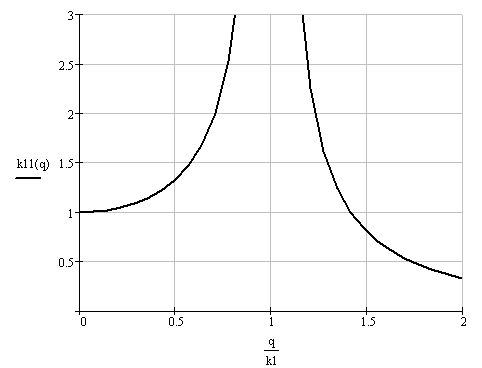
Рисунок 2.13 – График коэффициента динамичности

При учете сил сопротивления движению коэффициент динамичности определяется формулой:

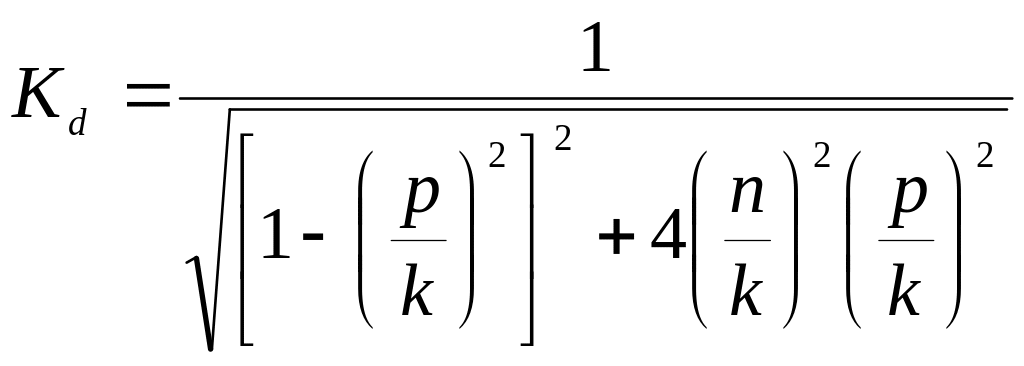(2.53)

Построим график коэффициента динамичности для двух случаев:

1) , тогда ;

2) , тогда .

Соответствующие графики приведены на рисунке 2.14.

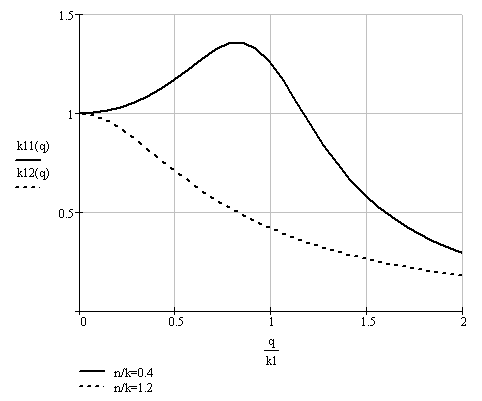
Рисунок 2.14 – Графики коэффициента динамичности при учете сил сопротивления

14