2.3 Вынужденные колебания

В случае вынужденных колебаний на точку действует возмущающая сила Q, которая изменяется по гармоническому закону, т.е. проекция ее на ось х определяется как:

где Н – максимальный модуль, или амплитуда возмущающей силы; р – частота изменения возмущающей силы, равная числу полных циклов изменения возмущающей силы за 2π с, – фаза изменения возмущающей силы; δ – начальная фаза изменения возмущающей силы.

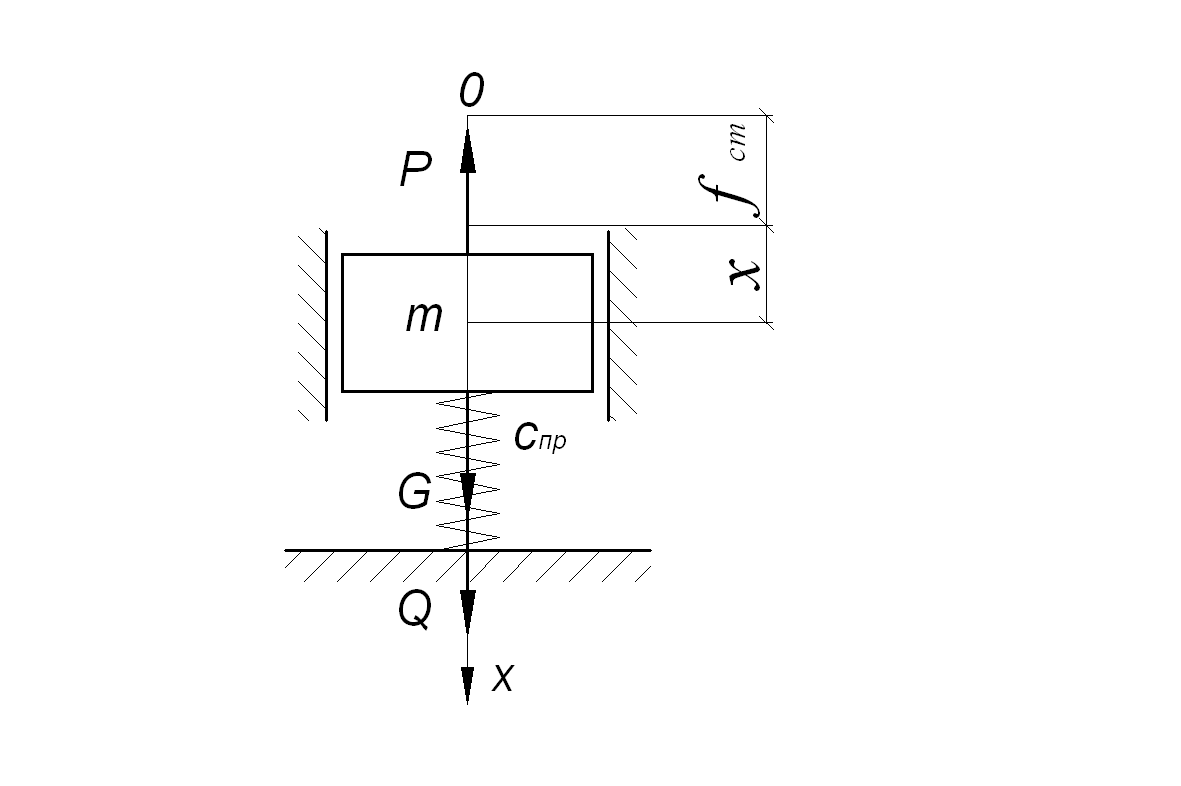
Рисунок 2.8 – Схема динамической системы

при вынужденных колебаниях

Период изменения возмущающей силы τ определяется по ее частоте:

Составим дифференциальное уравнение движения точки в проекции на ось х, учитывая, что на точку М с координатой х в момент времени t действуют силы Р и Q (рисунок 2.8):

Учитывая значения сил, получим:

, или

(2.35)

Здесь - квадрат частоты свободных колебаний.

Введем обозначение . Тогда:

(2.36)

Уравнение (2.36) представляет собой дифференциальное уравнение вынужденных колебаний материальной точки.

Решение уравнения (2.36) складывается из общего решения однородного уравнения и частного решения данного уравнения:

где х₁ – общее решение линейного однородного уравнения ;

х₂ – частное решение данного уравнения.

Однородное уравнение имеет решение:

В соответствии с видом функции f(t) в правой части уравнения будем искать частное решение в виде:

(2.37)

Определим постоянную А_В подстановкой функции (2.37) в уравнение (2.36). Так как , то после подстановки получаем:

Полученное равенство должно быть справедливо при любом значении . Это выполняется лишь при равенстве коэффициентов в левой и правой частях, т.е.

,

откуда

(2.38)

Подставляя значение А_В в выражение (2.37), находим искомое частное решение уравнения:

(2.39)

Уравнение (2.39) справедливо для случая, когда k > p. В этом случае имеют место вынужденные колебания малой частоты. Если же k < p (вынужденные колебания большой частоты), то тогда:

(2.40)

Решение уравнения (2.36) будет иметь вид:

(2.41)

Если же решению однородного уравнения придать вид , то решение уравнения (2.36) будет выглядеть как

(2.42)

Продифференцируем уравнение (2.41) по времени:

(2.43)

Определим значения констант интегрирования С₁ и С₂, подставив в уравнения (2.41) и (2.43) начальные условия: t=0: x=x₀, :

,

откуда найдем:

Для исходных данных при амплитуде возмущающей силы получим:

при вынужденных колебаниях малой частоты:

рад/с

м

Уравнение движения:

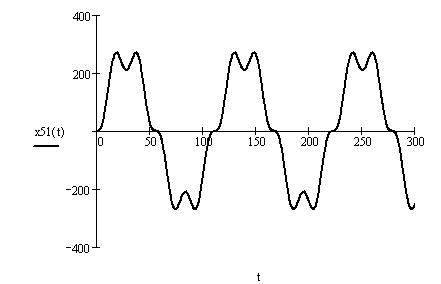
Графики вынужденных колебаний в случае, когда k > p показаны на рисунке 2.9.

а) б)

Рисунок 2.9 – Графики вынужденных колебаний при :

а) суммарный ;

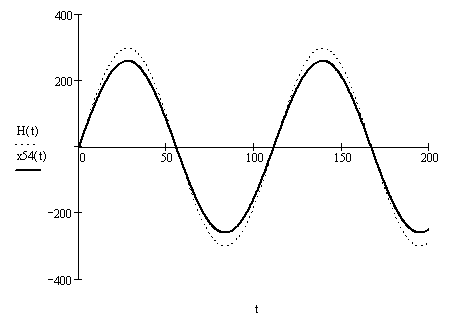
б) вынуждающей силы Н и перемещения х₂

при вынужденных колебаниях большой частоты:

рад/с

м

Уравнение движения:

(2.44)

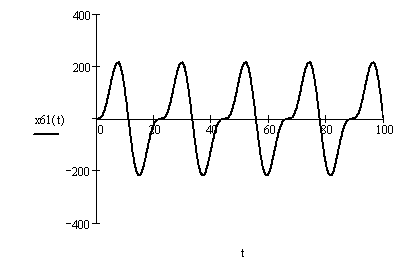
Графики вынужденных колебаний в случае показаны на рисунке 2.10.

Рисунок 2.10 – Графики вынужденных колебаний при :

а) суммарный ;

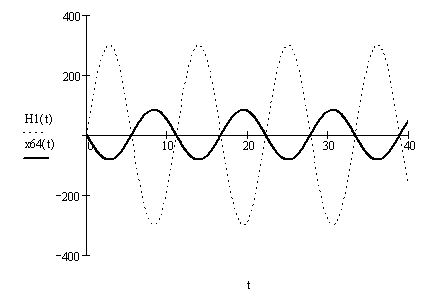
б) вынуждающей силы Н и перемещения х₂