2.2 Затухающие колебания

В случае затухающих колебаний на материальную точку кроме восстанавливающей силы Р действует сила сопротивления движению R, проекция на ось х которой:

(2.16)

где α – коэффициент сопротивления движению.

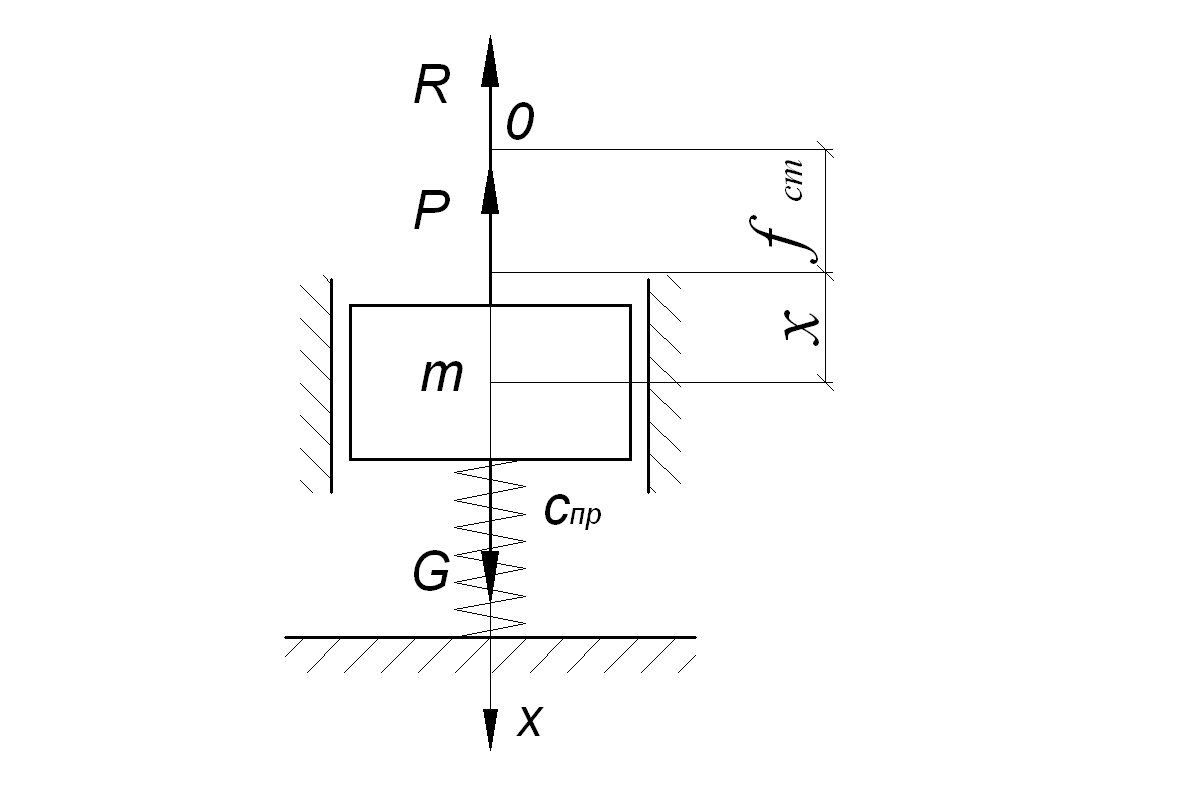
Рисунок 2.4 – Схема системы с учетом силы сопротивления

Составим дифференциальное уравнение движения материальной точки под действием сил Р и R (рисунок 2.4):

или

(2.17)

Введем обозначения , , тогда уравнение движения примет вид:

(2.18)

Здесь n – коэффициент затухания.

Решение уравнения (2.18) будем искать в виде: , тогда , . Подставив полученные выражения в уравнение (2.18), получим характеристическое уравнение:

Корни характеристического уравнения равны:

,

Дальнейший ход решения зависит от соотношения величин n и к.

Рассмотрим первый случай, когда n < k (n = 0,4k = 0,113 рад/с). В этом случае корни характеристического уравнения – комплексные числа:

,

где – циклическая частота затухающих колебаний.

Общее решение уравнения (2.18) в этом случае будет иметь вид:

(2.19)

Введем вместо констант С₁ и С₂ другие постоянные А и β, положив:

Подставив эти значения С₁ и С₂ в уравнение (2.19), будем иметь:

(2.20)

Движение, определяемое уравнением (2.20), имеет колебательный характер, так как координата х периодически изменяет свой знак вследствие изменения знака синуса. Множитель указывает на то, что амплитуда колебаний с течением времени уменьшается.

Величины А и β как постоянные интегрирования определяются по начальным условиям задачи. Чтобы найти А и β, продифференцируем уравнение (2.20) по времени:

(2.21)

Подставим в уравнения (2.20) и (2.21) начальные условия движения: t = 0: x = x₀, :

,

или

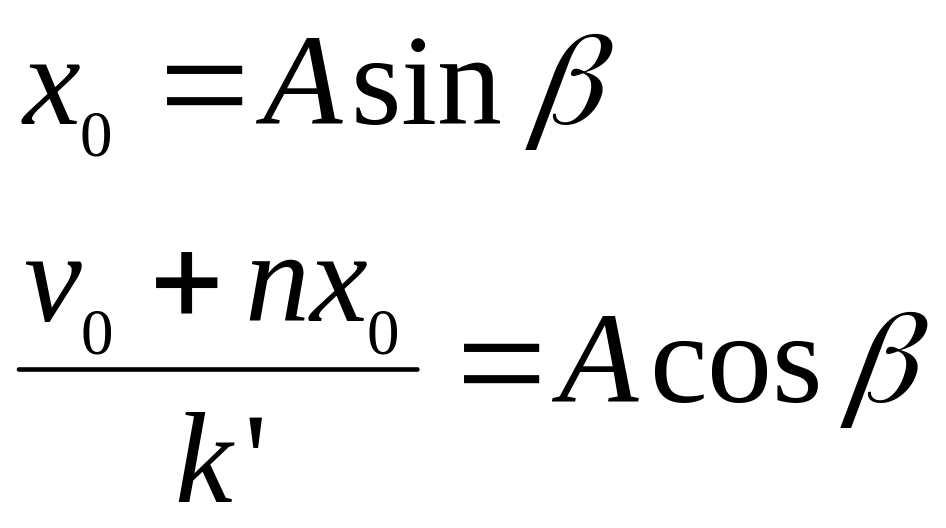
Откуда

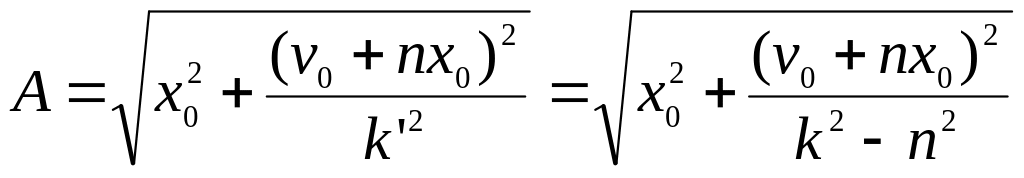(2.22)

(2.23)

Для исходных данных получим:

м.

Период затухающих колебаний Т’ определяется по формуле:

(2.24)

Тогда для исходных данных будем иметь:

рад/с,

с.

График затухающих колебаний в случае, когда n < k, изображен на рисунке 2.5.

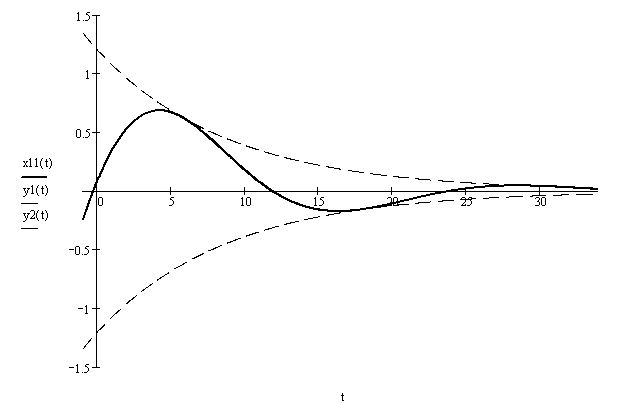
Рисунок 1.5 – График затухающих колебаний

Рассмотрим второй случай, когда n > k (n = 1,4k = 0,396 рад/с).В этом случае корни характеристического уравнения (2.18) имеют вид:

, (2.25)

И тогда решение уравнения (2.18) примет вид:

(2.26)

Введем вместо постоянных интегрирования С₁ и С₂ новые В₁ и В₂, положив:

Подставим эти значения С₁ и С₂ в уравнение (2.26):

.

Введем в полученное уравнение гиперболические функции:

,

Тогда получим уравнение:

Заменив В₁ и В₂ другими постоянными А и β по условию:

будем иметь уравнение движения в виде:

(2.27)

Уравнение движения точки (2.27) показывает, что рассматриваемое движение точки не является колебательным, так как гиперболический синус не является периодической функцией.

Перепишем уравнение (2.26) в виде:

(2.28)

где .

Продифференцировав последнее уравнение по времени, получим:

(2.29)

Подставив в уравнения начальные условия, будем иметь:

Откуда константы интегрирования:

,

Для исходных данных получим следующие расчеты:

рад/с;

,

И тогда уравнение движения (2.28) приобретает вид:

(2.30)

На рисунке 2.6 показан график движения точки с начальной скоростью , имеющей направление, совпадающее с направлением оси х. Благодаря этой скорости точка сначала удаляется от положения покоя, а затем под действием восстанавливающей силы постепенно приближается к этому положению.

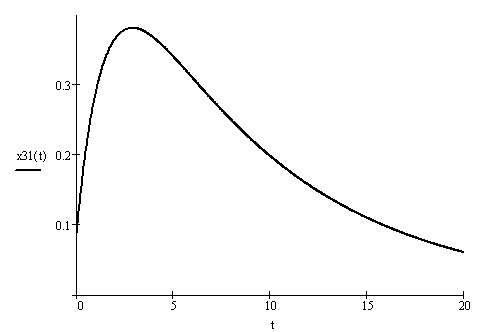
Рисунок 2.6 – График апериодического движения при n > k

Рассмотрим третий возможный случай, когда n = k. В этом случае корни характеристического уравнения вещественны, отрицательны и равны:

Общее решение уравнения (2.18) имеет вид:

(2.31)

Для определения констант интегрирования С₁ и С₂ продифференцируем последнее уравнение по времени:

(2.32)

Подставим в уравнения (2.31) и (2.32) начальные условия движения: t = 0: x = x₀, :

откуда

,

Зная значения С₁ и С₂, получим уравнение движения в виде:

(2.33)

Движение точки, определяемое уравнением (2.33), является также апериодическим. С учетом исходных данных оно получает вид:

(2.34)

График движения согласно уравнению (2.34) показан на рисунке 2.7.

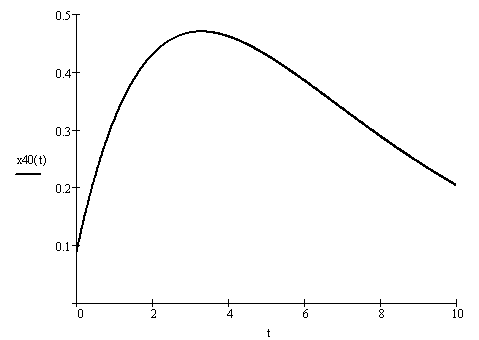
Рисунок 2.7 – График апериодического движения при n = k